武汉理工大学-数据结构与算法-(4)图的操作
文章目录
- 实验1:图的遍历及其生成树
- 实验目标
- 存储结构
- 深度优先搜索 DFS
- 广度优先搜索 BFS
- 源代码整合
- 运行结果
- 实验2:图的连通域
- 实验目标
- 存储结构
- 计算连通域个数
- 源代码整合
- 运行结果
- 实验3:图的最小生成树
- 实验目标
- 存储结构
- Prim算法
- Kruskal算法
- 源代码整合
- 运行结果
- 实验4:图的最短路径
- 实验目标
- 存储结构
- Dijkstra算法
- 源代码整合
- 运行结果
- 写在最后
实验1:图的遍历及其生成树
实验目标
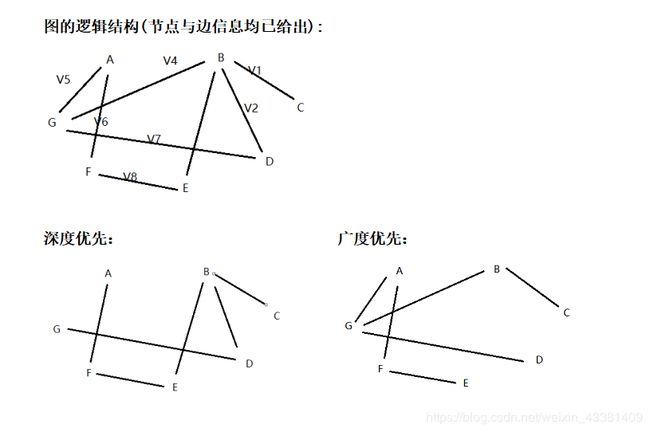
选择合适的结构存储图,编写程序,
实现图的两种遍历方法:深度优先搜索 和 广度优先搜索,并输出对应的生成树。
存储结构
//结构体_弧边
typedef struct Arc {
Info name; //弧边名称
int weight; //弧边权重
}Arc;
//结构体_节点
typedef struct Node {
Info name; //节点名称
int index; //节点序号
bool visited; //访问标记
}Node;
//结构体_图
typedef struct Graph {
Arc AdjMatrix[MAX_NUM][MAX_NUM]; //邻接矩阵
Node Nodes[MAX_NUM]; //节点数组
int Arc_Num; //弧边数量
int Node_Num; //节点数量
}Graph;
本实验采用 邻接矩阵 结构进行存储:使用 二维结构体数组 ,矩阵的行列序号表示连接边的起点和终点的序号。
深度优先搜索 DFS
//深度优先搜索 时间复杂度: O(Arc_num+Node_num)
void DFSTraverse(Graph &G, int n, bool(*Visit)(Node &N))
{
//参数n表示由第n号节点开始遍历
Visit(G.Nodes[n]);
for (int i = 0; i < G.Node_Num; i++) {
//若存在通路且另一节点未访问过
if (G.AdjMatrix[n][i].weight > 0 && !G.Nodes[i].visited) {
//打印弧边信息
cout << G.AdjMatrix[n][i].name << " ";
//递归访问
DFSTraverse(G, i, PrintNodeInfo);
}
}
}
深度优先搜索采用 递归 算法实现,由图的某一个结点开始 逐个分支地尽可能延伸 ,其 Visit 访问结点函数如下:
//打印节点信息
bool PrintNodeInfo(Node &n)
{
n.visited = true;
cout << n.name << " ";
return true;
}
访问结点函数将结点信息打出后,会将其 visited 标记置为 true,表示已访问,防止后续重复访问同一个结点。
深度优先搜索也可采用 堆栈 结构实现。
广度优先搜索 BFS
//广度优先搜索 时间复杂度: O(Arc_num+Node_num)
void BFSTraverse(Graph &G, int n, bool(*Visit)(Node &N))
{
Node u;
queue<Node> q; //辅助队列
Visit(G.Nodes[n]);
q.push(G.Nodes[n]); //入队
while (!q.empty()) {
//返回队首元素,并出队
u = q.front();
q.pop();
for (int i = 0; i < G.Node_Num; i++) {
//u.index 元素的序号
if (G.AdjMatrix[u.index][i].weight > 0 && !G.Nodes[i].visited) {
//打印弧边信息
cout << G.AdjMatrix[u.index][i].name << " ";
//访问
Visit(G.Nodes[i]);
//入队
q.push(G.Nodes[i]);
}
}
}
}
广度优先搜索采用 队列 结构实现,由某一个结点开始,一层一层地向周围点延伸 。
其 Visit 访问结点函数与深度优先搜索相同。
源代码整合
#define MAX_NUM 20 //最大节点数量
#define Info string //弧边与节点的信息
#include 图的信息可以在 InitGraph 函数里进行修改 。
运行结果
实验2:图的连通域
实验目标
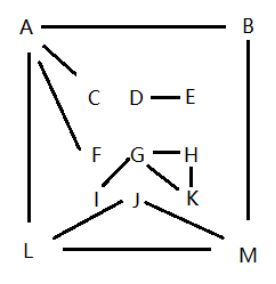
选择合适的存储结构,编写程序,建立图结构,并求出其连通域个数、各连通域的节点与弧边。
存储结构
//结构体_弧边
typedef struct Arc {
Info name; //弧边名称
int weight; //弧边权重
}Arc;
//结构体_节点
typedef struct Node {
Info name; //节点名称
int index; //节点序号
int connect; //连通域序号
bool visited; //访问标记
}Node;
//结构体_图
typedef struct Graph {
Arc AdjMatrix[MAX_NUM][MAX_NUM]; //邻接矩阵
Node Nodes[MAX_NUM]; //节点数组
int Arc_Num; //弧边数量
int Node_Num; //节点数量
}Graph;
增加了 connect 连通域序号标记 。
计算连通域个数
//打印节点信息
bool PrintNodeInfo(Node &n, int count)
{
n.visited = true;
n.connect = count; //标记连通域
cout << n.name << " ";
return true;
}
//深度优先搜索
void DFSTraverse(Graph &G, int n, int count)
{
PrintNodeInfo(G.Nodes[n], count);
for (int i = 0; i < G.Node_Num; i++) {
if (G.AdjMatrix[n][i].weight > 0 && !G.Nodes[i].visited) {
cout << G.AdjMatrix[n][i].name << " ";
DFSTraverse(G, i, count);
}
}
}
//计算图的连通域
int Connection(Graph &G)
{
//连通域计数
int count = 0;
//对节点数组遍历
for (int i = 0; i < G.Node_Num; i++) {
if (G.Nodes[i].visited) continue; //若已访问则跳过
else {
cout << "连通域" << ++count << ":";
DFSTraverse(G, i, count); //利用深度优先搜索标记连通域
cout << endl;
}
}
return count;
}
计算连通域个数的方法很简单,对图的结点数组进行遍历,利用深度优先搜索对结点的 connect 进行标记 。
源代码整合
#define MAX_NUM 20 //最大节点数量
#define Info string //弧边与节点的信息
#include 同样的,图的信息可以在 InitGraph 函数里修改。
运行结果
实验3:图的最小生成树
实验目标
编写程序,实现某个图结构的 最小生成树,
利用 Prim 和 Kruskal 两种算法,将树的节点与弧边打出。
存储结构
//结构体_弧边
typedef struct Arc {
Info name; //弧边名称
int weight; //弧边权重
int x, y; //弧边在邻接矩阵中的坐标
}Arc;
//结构体_节点
typedef struct Node {
Info name; //节点名称
int index; //节点序号
int visited; //访问标记
}Node;
//结构体_图
typedef struct Graph {
Arc AdjMatrix[MAX_NUM][MAX_NUM]; //邻接矩阵
Node Nodes[MAX_NUM]; //节点数组
int Arc_Num; //弧边数量
int Node_Num; //节点数量
}Graph;
为弧边增加了在邻接矩阵内的位置坐标x、y,也就是连接的两个结点的序号。
Prim算法
//---------------------------------------------------------------
//Prim算法 时间复杂度:O(Node_Num^2)
int MiniSpanTree_Prim(Graph &G, int n)
{
//用于存储与生成树连通域相邻的边
vector<Arc> CloseArcs;
int count = G.Node_Num; //循环次数
int weight = 0; //权重
//由第n号节点开始生成最小树
G.Nodes[n].visited = true;
//由第p号节点开始扩展边
int p = n;
while (--count) {
//扩展与生成树连通域相邻的弧边,并存储这些弧边
for (int i = 0; i < G.Node_Num; i++) {
if (G.AdjMatrix[p][i].weight > 0 && G.AdjMatrix[p][i].weight < INT_MAX) {
CloseArcs.push_back(G.AdjMatrix[p][i]);
}
}
//寻找最小权值
int min = INT_MAX;
int k;
//对连通域相邻边集合遍历
for (int i = 0; i < CloseArcs.size(); i++) {
Arc L = CloseArcs[i];
int w = L.weight;
//如果权值小于min大于0,而且连接边的两节点一个已访问一个未访问(防止形成环路)
if (w < min&&w>0 && !(G.Nodes[L.x].visited&&G.Nodes[L.y].visited)) {
min = w;
k = i;
}
}
//增加权值
weight += min;
//最小权值的边,通过该边y坐标找到下一个扩展点
Arc A = CloseArcs[k];
p = A.y;
//将另一未访问节点设为已访问
G.Nodes[p].visited = true;
//打印扩展过程
cout << G.Nodes[A.x].name << "-" << A.name << "-" << G.Nodes[A.y].name << " ";
}
return weight;
}
Kruskal算法
//-------------------------------------------------------
//修改sort的Compare函数
bool Compare(Arc A1, Arc A2)
{
return A1.weight < A2.weight;
}
//创建查并集
void MakeSet(vector<int> &uset, int n)
{
//将n个0值装到vector容器中
uset.assign(n, 0);
//初始化容器, 第i号元素为i
for (int i = 0; i < n; i++) uset[i] = i;
}
//查找当前元素所在集合的代表元
int FindSet(vector<int> &uset, int u)
{
int i = u;
while (uset[i] != i) i = uset[i];
return i;
}
//Kruskal算法 时间复杂度:O(Arc_Num * log(Arc_Num))
int MiniSpanTree_Kruskal(Graph &G)
{
//权值
int weight = 0;
//标记不同的连通域,用查并集模式存储
vector<int> uset;
MakeSet(uset, G.Node_Num);
//获取矩阵上三角部分,获得所有边的信息
vector<Arc> Arcs;
for (int i = 0; i < G.Node_Num; i++) {
for (int j = i + 1; j < G.Node_Num; j++) {
if (G.AdjMatrix[i][j].weight > 0 && G.AdjMatrix[i][j].weight < INT_MAX) {
Arcs.push_back(G.AdjMatrix[i][j]);
}
}
}
//对各边按权值由小到大排序
sort(Arcs.begin(), Arcs.end(), Compare);
//由小到大遍历
for (int i = 0; i < Arcs.size(); i++) {
//找到边连接两个点分别属于哪个连通域
int e1 = FindSet(uset, Arcs[i].x);
int e2 = FindSet(uset, Arcs[i].y);
//如果连通域不相同
if (e1 != e2) {
//打印生成过程
cout << G.Nodes[Arcs[i].x].name << "-" << Arcs[i].name << "-" << G.Nodes[Arcs[i].y].name << " ";
//权值增加
weight += Arcs[i].weight;
//连通域并集操作(重点)
uset[e1] = e2;
}
}
return weight;
}
将两个连通域归并时利用 查并集操作,读者可以注意一下。
源代码整合
#define MAX_NUM 20 //最大节点数量
#define Info string //弧边与节点的信息
#include 图的信息可在 InitGraph 里修改。
运行结果
实验4:图的最短路径
实验目标
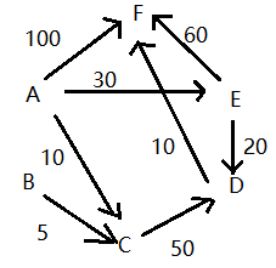
选择合适的存储结构存储某个有向图,编写程序,计算某一节点到其他节点各自的最短路径是多少。
存储结构
//结构体_弧边
typedef struct Arc {
Info name; //弧边名称
int weight; //弧边权重
int x, y; //弧边在邻接矩阵的坐标
}Arc;
//结构体_节点
typedef struct Node {
Info name; //节点名称
int index; //节点序号
int visited; //访问标记
}Node;
//结构体_图
typedef struct Graph {
Arc AdjMatrix[MAX_NUM][MAX_NUM]; //邻接矩阵
Node Nodes[MAX_NUM]; //节点数组
int Arc_Num; //弧边数量
int Node_Num; //节点数量
}Graph;
Dijkstra算法
本实验采用经典的 Dijkstra 算法 计算最短路径:
//Dijkstra算法 时间复杂度:O(Node_Num^2) 计算从v0点到图中其余各点的最短路径
void ShortestPath_DIJ(Graph &G, int v0)
{
//Distance[i]表示v0点到i点的最短距离
int Distance[MAX_NUM];
//Final[i]表示是否已求出v0点到i点的最短距离
bool Final[MAX_NUM];
//初始化
for (int i = 0; i < G.Node_Num; i++) {
Final[i] = false;
Distance[i] = G.AdjMatrix[v0][i].weight;
}
//初始化,v0点属于连通集S
Final[v0] = true;
int v; int min;
//剩余G.Node_Num-1个点待计算
for (int i = 1; i < G.Node_Num; i++) {
//为防止溢出,min不再使用INT_MAX
min = 10000;
for (int j = 0; j < G.Node_Num; j++) {
//如果点j属于G-S,且与连通域有通路
if (!Final[j] && Distance[j] < min) {
//计算最短路径
min = Distance[j];
//若有最短路径则用v标记改点
v = j;
}
}
//将v点加入连通集S
Final[v] = true;
//更新当前最短路径
for (int w = 0; w < G.Node_Num; w++) {
//对于G-S的点x,Distance[x] = min{ D(v0,v) + D(v,x) , D(v0,x) }
if (!Final[w] && (min + G.AdjMatrix[v][w].weight < Distance[w])) {
Distance[w] = min + G.AdjMatrix[v][w].weight;
}
}
}
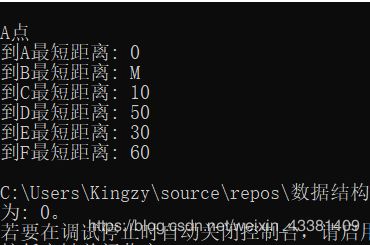
//打印到各点的距离
cout << G.Nodes[v0].name << "点" << endl;
for (int i = 0; i < G.Node_Num; i++) {
cout << "到" << G.Nodes[i].name << "最短距离: ";
if (Distance[i] >= 10000) cout << "M" << endl;
else cout << Distance[i] << endl;
}
}
源代码整合
#define MAX_NUM 20 //最大节点数量
#define Info string //弧边与节点的信息
#include 图的信息可在 InitGraph 函数里修改,起始结点通过可以修改 v0 参数实现。
运行结果
写在最后
声明:本文内容来源于武汉理工大学2019-2020学年数据结构与算法课程实验,仅供学习参考。如有不足地方,还请指出。
代码不要无脑抄 ,建议理解思路。祝愿读者能够在编程之路上不断进步!