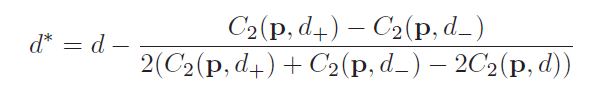双目立体匹配 等 算法 论文 综述 全局局部算法 CSCA NLCA SegmentTree树 DoubleBP Belief-Propagation AD-Census SGM

双目立体匹配 等 算法 论文 综述

本文GITHUB

博文末尾支持二维码赞赏哦 ^_

双目立体视觉技术实质就是模拟人的双眼视觉处理系统来处理通过摄像机采集所
获取的图像，它利用两台或多台摄像机在一定约束条件下采集同一场景的图像，对采集
到的图像进行信息提取和整合，最终恢复图像中场景的三维信息。 

基于双目视觉的立体匹配算法研究涉及模式识别、人工智能、机器视觉、计算机图
形学等领域的许多相关复杂的研究课题。随着许多著名专家学者对此问题不断深入地研
究，立体匹配算法的精度越来越高，实时性越来越好。

kitti双目算法评测

Middlebury Stereo Evaluation - Version 2 算法评测

立体匹配的研究背景以及意义

立体匹配导论

三维重建技术概述 pcl 点云配准

三维重建基础 背景意义 双目立体视觉 tof 结构光

机器人视觉技术中所涉及的立体匹配通常是指应用于机器人立体视觉系统 
中的一项关键技术，是指采用行之有效的方法来分析从不同的视角条件下获取 
的目标物体的左右图像（图像对）之间的一致性或相似性，并识别出左右图像 
（图像对）间的对应点或同名点； 立体匹配技术都是指应用于机 
器人双目立体视觉系统中的。

当三维空间场景中的标定物被投影为二维图像时，二维图像信息丢失了标定物的深度信息 z，
立体匹配就是要恢复物体的深度信息 z，它是模拟人的双眼感知外部事物的过程。
具体来讲，立体匹配是对所选图像对中的图像特征点的计算，来建立不同图像特
征空间点中的像素对应关系。换句话说，就是将世界坐标系中的空间特征点与图像坐标
系中相对应的图像特征点进行一一映射，经过匹配算法等处理计算出空间特征点的三维
坐标，最终获得其对应的视差图。在视差图中，所得的是图像某一点以像素为单位的视
差值，它一般是一个整数估计值，由是差值就可得到场景的深度信息。 


根据采用最优化理论方式的不同，立体匹配算法又分为基于局部的立体匹配算法和基于全局的立体匹配算法。
基于局部的立体匹配算法的核心在于匹配代价的计算和代价聚合阶段。
基于全局的立体匹配算法在视差计算阶段处理算法中的大部分计算问题，最终得到的视差图精准度更高，
基本上满足人们在实际生产应用中对匹配精度的要求

全局

基于全局的立体匹配算法使用全局约束来解决由于遮挡或重复纹理造成的像素误
匹配问题，是基于优化理论方法估计视差值。全局匹配问题通常被描述为能量最小化问
题，在其建立的能量函数中，除了数据项之外，还有平滑项。数据项主要是测量像素之
间的相似性问题，而平滑项是平滑像素之间的视差关系，保证相邻像素之间视差的平滑
性.基于全局的立体匹配算法需要构造一个能量函数，其形式一般为：

E = Edata + Esmooth

其中数据项 Edata 描述了匹配程度，平滑项 Esmooth体现了场景中的各种约束。

基于动态规划的立体匹配算法

全局立体匹配算法中动态规划算法是使用比较多的一种经典算法，
传统的动态规划立体匹配算法基于极线约束，
在每条极线上面运用动态规划方法来寻找最佳匹配点，
并通过动态寻优的方法来寻求全局能量最小化，得到视差匹配图。
但由于只是扫描了水平极线上像素点，导致视差图的条纹现象十分明显。

ＫｕｎｐｅｎｇＬｉ通过先提取图像中的特征点，然后将特征点用最近邻搜索算法进行匹配的
方法，以缓解传统的动态规划算法引起的横条纹效应；为了更加高效的利用动态规划立体匹配
算法，ＣａｒｌｏｓＬｅｕｎｇ提出了一种快速最小化方案，通过使用迭代动态规划算法来进行立体匹
配，该算法对行和列进行迭代以达到实现快速立体匹配的目的；ＴｉｎｇｂｏＨｕ考虑到动态规划
匹配算法对图像边缘不能有效匹配的问题，将单一的极线搜索改进成单向四连接树的匹配算
法，并针对ＳＤＦＣ树设计了快速动态规划优化方法，这样可以在有效的提高匹配精度的同时，
将计算复杂度降低到传统动态规划算法的１／１２。

基于图割法的立体匹配算法

图割法是一种能量优化算法，通过一个无向图来表示要分割的图像，并利用Ｆｏｒｄ和Ｆｕｌｋ－
ｅｒｓｏｎ的最大流－最小割理论求出最小割，也就是最优的图像分割集合，
通过该方法可以很好的解决动态规划引起的条纹现象，但是缺点是时间复杂度比较大。
颜轲先将图像进行分割并建立立体匹配的马尔科夫有随机场模型，然后通过约束条件
保留分割的信息，提高了匹配的精度；Ｌｅｍｐｉｔｓｋｙ通过将图像进行最优分割，然后对分割后
的图像进行分别计算，最后将结果进行结合，确保准确率不会下降的情况下，大大提高图割法的运行速度.

基于置信度传播的立体匹配算法

置信度传播的立体匹配算法由马尔科夫随机场模型组成。其将像素点作为网络传输的节点，
每个节点包含数据信息和消息信息两种，分别保存像素的视差值和每个节点的信息值。
置信度传播算法通过像素在四邻域网格上进行，在匹配的时候设定编号的模型，
通过对编号相同的点进行搜索。它的消息值是自适应的，在低纹理区域能够将消息传播到很远。
虽然匹配的精度提高了，但由于单个像素点容易产生误匹配，并且进行的是全局图像像素的搜索，
算法时 间复杂度非常大。因此如何快速有效的运用该算法也成为了研究的热点。

局部

基于局部的立体匹配算法采用局部优化的理论方法进行像素视差估计，研究的重点
在于匹配代价的计算和匹配代价的累积上。它是在最大视差的范围内找出匹配代价最小
的像素点作为目标匹配像素，利用局部信息求出匹配代价最小的像素点从而计算出视
差。与全局立体匹配算法相同，这类算法是通过寻找能量最小化方法进行像素视差估计，
但是，在能量函数中只有数据项没有平滑项。实时立体视觉系统多采用匹配速度较快的
局部匹配算法来处理获得的图像。 
基于局部的立体匹配算法主要有 SSD、SAD 等算法，大致可以分为三类：自适应
窗体立体匹配算法、自适应权值立体匹配算法和多窗体立体匹配算法。
这些算法都是从邻域像素中选择最佳的支持区域和支持像素，即尽可能选择与要计算像素具有相同真实
视差的像素点作为其支持像素，利用支持像素作为邻域约束条件，从而得到比较好的局
部视差估计。自适应窗体是窗体在自适应进行变化，包含大小和形状，针对不同的变化
规则就具有不同的算法。多窗体匹配算法，主要是从多个窗体中，按照一定的规则，选
择最佳的窗体进行视差估计。自适应权值的立体匹配算法，主要是建立邻域像素的真实
支持度关系，根据它们的属性的不同建立不同的支持度模型，能反映他们之间真实的视
差关系。 

基于区域的立体匹配算法

基于区域的立体匹配算法通过确定源图像上一个像素点，并在该像素点周围选取一个子
窗口，然后在目标图像的区域内寻找与该子窗口最为相似的窗口，匹配得到的窗口对应的像素
点就是该像素的匹配点。该算法在时间复杂度上比较小，但是对于弱纹理区域匹配效果不太
理想，受环境影响比较大，比如光照、遮挡等影响。并且在进行立体匹配的时候，子窗口大小的
选择也成为一个难点。
现在普遍利用视差估计、窗口视差近似等方法获得具有自适应的窗口，并在此基础上改进
算法。曾凡志在自适应窗口的基础上，采用８个相同的窗口运用并行处理的方法，根据图
像的平滑情况从８个方向选择合适的区域，该算法解决了在低纹理区域容易造成误匹配的现
象，并且运行时间与传统时间差别不大；ＺＦ Ｗａｎｇ将区域作为匹配的基元，通过引入区域之
间的合作和竞争，采用协作优化模式来最小化匹配成本。

于区域的图像匹配方法能够直接产生浓密的视差图，缺点是计算量大，实时性不强；

基于特征的立体匹配算法

基于特征的立体匹配算法主要利用图像的几何特征信息，根据特征信息进行视差的估计。
所以在进行匹配的时候，要先进行特征点的提取，并根据特征点建立物体的稀疏三维轮廓，
如果想要稠密的立体图则需要进行相应的插值算法。基于特征的立体匹配算法更多的强调的是
物体的结构信息，根据特征提取的不同，又可以分为基于点特征的匹配算法，
基于线特征的立体匹配等。

基于特征的图像匹配方法是针对摄像机获取的图像对中选取特定的特征点进行匹配，
其优点是匹配速度相对较快，匹配结果的精度也较高，
对于图像对中没有明显纹理等特征的区域容易造成歧义匹配而无法处理；

基于相位的匹配

是利用相位信号作为匹配基元，它可以精确到对每个像素的匹配，
经过特殊处理后，一般只能得到空间场景中标定物的大致结构.

基于相位的立体匹配算法是在频率区域范围内对相位信号进行视差估计，算法假定
图像对中的对应像素点附近在其频率范围内局部相位是相等的，从频率域相位的角度来
进行像素点视差值的估计。相位信号在空间域上的平移现象在频率域中表现为成比例
的相位平移，主要依据是傅立叶平移定理。该类算法对于各种畸变，如几何畸变和辐射
畸变等，具有很好的抗干扰能力，所以基于相位的匹配算法能够获得亚像素级的致密视
差图。徐彦君提出了一种基于相位的尺度自适应的立体匹配方法，尺度自适应是一种基
于频率响应积分面积相关的选择规则，实现了一种新颖的尺度自适应算法，对于常见的
“卷积
”问题，采用
“由粗及细
”的逐步求精方法处理，该方法获得的视差图有精度高、稳
定性好等优点，且能预测很大的视差范围。 

经典立体匹配算法对比表

         立体匹配算法名称                 算法特性
    基于动态规划的立体匹配算法      时间复杂度比较低，匹配精度不高，容易出现条纹现象
    基于图割法的立体匹配算法        能解决动态规划出现的条纹现象，边缘匹配处理比较好，时间复杂度比较高
    基于置信度传播的立体匹配算法    收敛性比较差，时间复杂度比较高，对于低纹理问题处理的比较好
    基于区域的立体匹配算法          时间复杂度比较低，算法受环境影响比较大，弱纹理问题不能有效解决
    基于特征的立体匹配算法          时间复杂度比较低，对于几何特征明显的图像匹配效果比较好

3 个基本问题

1)  匹配基元的选择：
    选择合适的图像特征点、特征线或特征区域等作为匹配基元，使匹配结果更准确； 

    匹配基元是指在图像中有明显特征的点、线或者特定的区域，它是立体匹配算法的
    最小匹配单元。由于在双目立体视觉系统中采集图像阶段经常受到摄像机的角度和位
    置、场景纹理的特征和数量和光照的强弱变化程度等外在因素的影响，因此要在获取的
    图像对中对所有的像素点都进行无歧义性的匹配是有难度的。 
    
    前常用的匹配基元有：过零点（zero-crossing）、边缘轮廓（object  boundaries）、
    线性特征（linear features）、像素灰度值等，
    从总体上大致分为：
    点状特征、区域特征和 线状特征.
    
    其中，点状特征是最基本的特征基元，所含有效的信息量相对较少；
    区域特征基元具有较好的全局属性，所含的信息量较为丰富，能够简单描述出事物的大致结构；
    线状特征基元是介于两者之间的。 
    
    点状特征基元的优点是对特征点定位准确、检测和描述像素点的信息更容易，在合
    适的图像中可以采用点状特征基元对场景进行三维重建。采用点状特征作为基元的算法
    需要采用比较有力的约束准则及匹配策略来约束像素点，通常选择图像中的角点作为点
    状特征匹配基元。 


2)  匹配准则：
    将客观世界中存在的事物固有的属性作为匹配算法必须遵循的准则，
    所得结果能够更真实的反映事物的原貌及特征； 
    
    极线约束、唯一性约束 、连续性约束 、顺序一致性约束
    
3)  算法结构：选择或设计合适的数学方法对匹配算法来说也是非常关键的一步，
    直接影响算法的执行效率。 

相似性测度

立体匹配中的相似性测度是衡量两幅或多幅图像中，参考图像中的匹配模板与待匹
配图像中区域之间的相似程度的度量，这个测度可以让我们找到最优的匹配区域。
专家和研究学者对立体匹配问题已研究经，也提出了一些关于相似性测度的标准及方法。
常见的有：最小值绝对差 
SAD（Sum of Absolute Difference）、
最小值平方差 SSD (Sum of Squared Difference)、
互相关 NCC （Normalized Cross Correlation）等多种测度

立体匹配算法的步骤

在双目立体视觉中，立体匹配是比较关键的部分，也是最困难和最复杂的部分，
其目的就是根据所选相似性测度，在待匹配图像中，找出参考图像某物点的对应匹配点，
建立双目图像间的特征对应关系，Ｗ此计算二者的视差并恢复图像深度信息。
立体匹配算法的研究重点主要在于匹配基元的选择、相似性测度函数、立体匹配策略和约束准则等。

1）匹配代价计算； 
2）匹配代价叠加； 代价聚合
3）视差获取；
4）视差细化（亚像素级）

基于全局的立体匹配算法一般不需要进行匹配代价的叠加，
而是利用匹配代价和平滑约束来实现全局能量最小化，通常不包含第 2步。
而基于局部的立体匹配算法是基于矩形窗口滑动的方法，
它以中心像素点的领域像素点灰度均值为矩形窗口进行匹配代价的叠加。

1. 匹配代价计算

SD AD Census
C(x, y, z) =L(x +d, y) −R(x, y) 
L 代表双目立体视觉系统中的左视图， 
R 为双目立体视觉系统中的右视
图， x和 y 分别表示像素点的坐标值，d像素点的视差值。
经过计算后得到的C 为三维矩阵，我们称它为视差空间 DSI(Disparity Space Image)，

视差空间 DSI 中任意的 d 对应有 x 和 y 的切面，
而该空间中(x, y,d) 的值表示参考图像中点(x, y) 被赋予视差 d 时的匹配代价m(x, y,d) 。

2. 匹配代价叠加/聚合

匹配代价的叠加是基于窗口的代价函数的叠加[7]。
基于区域的匹配算法它用来增强匹配代价的可靠性，
通常以待匹配像素为中心点选择一个矩形区域，将区域内的匹配代价与周围的匹配代价进行叠加。

根据原始匹配代价不同可分为 SSD(sum  of  squared differences)算法、
SAD(sum  of  absolute  differences)等。
对于给定支持域的像素的匹配代价聚集操作可以采用 2D 或 3D 卷积的形式进行.
C(x, y, d) = w(x, y, d) ∗ C0(x, y, d)
其中，C0(x, y, d) 为给定像素的支持域内某像素的匹配代价值， 
w(x, y, d) 表示支持域内给定像素的权值。
C(x, y,d) 为给定像素的新的匹配代价。

3. 视差获取

视差的获取的方法分为两类，一类是基于窗口的局部立体匹配算法，它只需在窗口
的范围内选择匹配代价聚集后的最佳点（最佳点的获取通常采用 SAD 或  SSD 算法结果 取最小值）作为对应的匹配点(WTA赢者通吃)。

另一类是基于全局的立体匹配算法，实质是获得能量函
数的最小值，算法先给出一个能量评价函数，然后通过优化算法来求得能量的最小值，
使能量函数最小的匹配关系即为最终的视差，同时可以获得每个像素的视差值。 

局部匹配算法只有数据项，并无平滑项。全局算法包含 数据项和平滑项。

平滑项分为两种情况，
一种是极线间平滑性，
另一种是极线方向平滑性，两者种情况的计算方法相同，
都采用基于邻域的视差值计算方法，
如极线方向平滑性的计算公式：
Esmooth = sum( ρ(d(x, y),d(x+1, y)) )

在视差图中存在视差深度不连续的情况，例如场景中的物体与其背景相交的区域。
由于视差深度不连续的情况一般都发生在图像的边缘区域。如果存在图像中的灰度值变
化较大的区域，通常采用降低平滑代价的方法解决。由于场景中物体与其边界处通常存
在 视 差 深 度 的 跳 变 ， 造 成 视 差 深 度 不 连 续.
ρ(d(x, y),d(x+1, y))
 ====> 改为
 ρ(d(x, y),d(x+1, y)) =  | 0   ， d(x,y) = d(x+1,y) ，     视差差1 而 代价相同  平滑处
                         | t   ， |d(x,y) - d(x+1,y)|=1    视差差1 而 代价额差1 ，  t为常数
                         | w   ，  其他情况 ， w 更加灰度差值大小确定

4. 视差修正

视差获取及优化步骤中得到的是估计的视差图，
由于遮挡、噪声和光强等因素的影响，匹配过程中不可避免的存在误匹配点。
估计视差图中存在一些离散的空白像素，需要对其做进一步修正。 
常用的修正方法有两种：
    一种是采用左右一致性检验的方法，
        该方法的步骤是对两幅图像中的匹配点分别检测并进行对比，
        若相同，说明该匹配点视差值是正确的，
        若不相同，则认为该点是误匹配点并对其进行校正处理。
    另一种是采用平滑滤波的方法，
        常用的平滑滤波是中值滤波，它将窗口内所有像素的灰度值从大到小排序，将排序后的
        中间值取出替代要误匹配的数据，让周围的像素值更接近的真实值，从而消除孤立
        的噪声点，达到视差修正的目的。 

面临的挑战

1. 遮挡区域的立体匹配。
2. 弱纹理或重复区域的立体匹配。歧义性(ambiguity)比较大。视差平面集合能近似表示场景的结构。
3. 深度不连续像素点的立体匹配。物体的边缘，简单的推理和插值
4. 照变化引起的立体匹配问题。没有考虑镜面反射的情况。
5. 倾斜区域的匹配问题。

图像分割

图像分割（Image segmentation）方法是近年来才引入立体视觉系统中，也是立体匹
配算法研究中的一个重要的研究方向，图像分割技术在复杂场景的图像识别、图像分析、
图像理解和表达等方面能够发挥其优势。图像分割的原理是对摄像机所拍摄场景中的图
像进行分析，根据一定相似准则分析出图像场景中的一些相类似的特征点或特征区域，
再根据一定的约束准则对图像中相似点或相似区域的像素进行分组并聚合，此时聚合后
的图像上会出现有特殊规律的区域。这些特殊的区域既使后续的图像高级处理（包括
图像识别、图像分析、图像理解和表达等）阶段的操作步骤大大减少，又能保持图像结
构特征的关键信息不丢失。针对立体匹配算法，将图像分割成一些具有相同特征的小区
域，而这些区域往往有一个平滑的视差，然后利用上述方法进行匹配就会得到更好的效果。 
研究者和专家们对图像分割技术的研究及方法在一直不断的探索改进中，
常见的图像分割算法有
    基于阈值分割、
    基于区域分裂合并、
    分水岭分割、
    均值漂移(Mean shift)、
    区域生长法、
    基于边缘检测的分割 以及
    基于聚类算法的分割等方法。
应用于立体匹配中的方法也有许多，其中均值漂移算法和分水岭分割法在立体匹配方面比较受研究者的青睐。

论文

1. CSCA 2014 多尺度代价聚合

论文： Cross-Scale Cost Aggregation for Stereo Matching

代码

参考博客

立体匹配最基本的步骤

1）代价计算 CC。
   计算左图一个像素和右图一个像素之间的代价。

2）代价聚合 CA。
   一般基于点之间的匹配很容易受噪声的影响，往往真实匹配的像素的代价并不是最低。
   所以有必要在点的周围建立一个window，让像素块和像素块之间进行比较，这样肯定靠谱些。
   代价聚合往往是局部算法或者半全局算法才会使用，
   全局算法抛弃了window，采用基于全图信息的方式建立能量函数。

3）深度赋值。
   这一步可以区分局部算法与全局算法，局部算法直接优化 代价聚合模型。
   而全局算法，要建立一个 能量函数，能量函数的数据项往往就是代价聚合公式，例如 DoubleBP。
   输出的是一个粗略的视差图。

4）结果优化。对上一步得到的粗估计的视差图进行精确计算，策略有很多，
例如plane fitting，BP，动态规划等。

可以看作为一种全局算法框架，通过融合现有的局部算法，大幅的提高了算法效果。

论文贡献

第一，设计了一种一般化的代价聚合模型，可将现有算法作为其特例。

第二，考虑到了多尺度交互（multi-scale interaction），
     形式化为正则化项，应用于代价聚合（costaggregation）。

第三，提出一种框架，可以融合现有多种立体匹配算法。

CSCA利用了多尺度信息，多尺度从何而来？
其实说到底，就是简单的对图像进行高斯下采样，得到的多幅成对图像（一般是5对），就代表了多尺度信息。
为什么作者会这么提，作者也是从生物学的角度来启发，他说人类就是这么一个由粗到精的观察习惯（coarse-to-line）。
生物学好奇妙！

该文献生成的稠密的视差图，基本方法也是逐像素的（pixelwise），
分别对每个像素计算视差值，并没有采用惯用的图像分割预处理手段，
如此看来运算量还是比较可观的。

算法流程

1. 对左右两幅图像进行高斯下采样，得到多尺度图像。

2. 计算匹配代价，这个是基于当前像素点对的，通常代价计算这一步并不重要，
   主要方法有CEN（Census,周围框,对窗口中每一个像素与中心像素进行比较，大于中心像素即为0，否则为1。从而得到一个二进制系列），
   CG（Census + TAD(三通道像素差值均值) + 梯度差值(灰度像素梯度差值)），
   GRD(TAD + 梯度差值)等几种，多种代价之间加权叠加

   得到的结果是一个三维矩阵
   左图 长*宽*视差搜索范围
   值为每一个匹配点对的匹配代价

3. 代价聚合,一个领域内的代价合并（聚合相当于代价滤波）
   BF（bilateral filter，双边滤波器 ），
   GF（guided image filter，引导滤波器），
   NL（Non-Local，非局部，最小生成树），
   ST（Segment-Tree，分割树，图论分割树） 等，

   基于滤波器的方法是设定一个窗口，在窗口内进行代价聚合。
   双边滤波器就是对窗口内像素进行距离加权和亮度加权。 

   后两种都抛弃了固定窗口模式，
   基于NL的代价聚合是使用最小生成树代替窗口。
   基于ST的代价聚合是使用分割块代替窗口。

   分割树ST代价聚合方法：
        a. 初始化一个图G（V，E）
           每个像素就是顶点V，边(E)是两个像素点对之间三通道像素差值绝对值中最大的那个，作为边的权值。

float CColorWeight::GetWeight(int x0, int y0, int x1, int y1) const {// 两个点对
//得到三通道两个像素值差值最大的那个通道的差值的绝对值,作为边测权重
return (float)std::max(
    std::max( abs(imgPtr(y0,x0)[0] - imgPtr(y1,x1)[0]), abs(imgPtr(y0,x0)[1] - imgPtr(y1,x1)[1]) ), 
    abs(imgPtr(y0,x0)[2] - imgPtr(y1,x1)[2])
    );

        b. 利用边的权值对原图像进行分割，构建分割树。
           先对边按权值大小进行升序排列
           判断边权值是否大于阈值，大于则不在同一个分割块，否则就在同一个分割块
        c. 对整颗树的所有节点计算其父节点和子节点，并进行排序。
        d. 从叶节点到根节点，然后再从根节点到叶节点进行代价聚合。

4. 多尺度代价聚合
   五层金字塔，利用上述方法对每一层计算代价-代价聚合
   添加正则化项的方式，考了到了多尺度之间的关系

   保持不同尺度下的，同一像素的代价一致，如果正则化因子越大，
   说明同一像素不同尺度之间的一致性约束越强，这会加强对低纹理区域的视差估计
   （低纹理区域视差难以估计，需要加强约束才行），
   但是副作用是使得其他区域的视差值估计不够精确。
   不同尺度之间最小代价用减法来体现，
   L2范式正则化相比较于L1正则化而言，对变量的平滑性约束更加明显。

5. 求最优视差值
   赢者通吃：winner-takes-all
   将每一个视差值代入多尺度代价聚合公式，选择最小的那个代价对应的视差值为当前像素视差值。

6. 视差求精
    1：加权中值滤波后，进行左右一致性检测; 
       进行不可靠点检测，找左右最近的有效点，选视差值较小的那个; 
       然后对不可靠点进行加权中值滤波; 
    2：分割后，进行左右一致性检测; 
       进行不可靠点检测，找左右最近的有效点，选视差值较小的那个; 
       然后进行对不可靠点进行加权中值滤波; 
       然后求分割块的平面参数，对分割块内的每个像素进行视差求精。

速度

在“CEN+ST+WM”组合下，
在640p的图像上，运行时间需要6.9s，
在320p的图像上，运行时间为2.1s，
在160p上，需要0.43s。

总结

1）CSCA是一个优秀的立体匹配算法，它的性价比，综合来说是比较高的，并且CSCA只是一个框架，
   言外之意，我们可以根据框架的思想自己创建新的算法，说不定能够获取更好的性能。
2）我认为CSCA是一个多尺度的局部算法，还不应该归类为全局算法的类别，这种多尺度思想，
   我想在今后的工作中会有越来越多的研究人员继续深入研究。

2. NLCA 算法 全局最小生成树代价聚合 (变形树局部框)

论文：A Non-Local Cost Aggregation Method for Stereo Matching

代码

参考

关键点

明确抛弃了support window（支持窗口）的算法思想，
指出support window在视察估计上普遍具有陷入局部最优的缺陷，
创新性的提出了基于全局最小生成树进行代价聚合的想法，我觉得这个想法非常厉害，全局算法早就有了，
但是往往是基于复杂的优化算法，重心放在了视察粗估计和迭代求精两步，十分耗时，而最小生成树，
可以天然地建立像素之间的关系，像素之间的关系一目了然，
可以大幅减少代价聚合的计算时间，文献表述为线性搜索时间。
计算聚合代价的过程不需要迭代，算法时间复杂度小，符合实际应用的需求，
所以NL算法已经获得了不错的引用率。
在后续算法中得到了很多改进，一些好的立体匹配算法，如CSCA，ST等都是基于NL进行了改进，
以下部分着重说说我对NL核心部分，最小生成树(minimum spanning tree，MST)的理解。

避免了局部最优解，找到了全局最优解。
其实MST就是一种贪心算法，每一步选择都是选取当前候选中最优的一个选择。

从一个顶点开始，选取一个最小边对应的顶点
从已经选取的顶点对应的连接顶点中选取最小的边对应的顶点。。。

最小生成树

prim（普里姆）算法：

代码

原地图：

修建步骤（从一点向外扩展，每次都选最小权重对应的边）：

kruskal（克鲁斯卡尔）算法:

代码

修建步骤（每次选出最小的边，不产生环，直到所有的顶点都在树上了）：

因为支持窗口的办法，本质上只考虑了窗口内像素对中心像素的影响，
窗口之外的像素的影响彻底忽略，其实想想看，这样做也没有什么不妥，
但是它并不适用一些场合，比如文献列举的图像，带纯色边框的一些图像。

左上角的图像就是原始灰度图像，这个时候我们就会发现，
这幅图像中像素与像素之间的关系用支持窗口来处理明显不灵，
比如说周围框状区域的任何一个像素，肯定与框状区域内部的像素的深度信息一致，
而与中间区域的像素不同。或者说，如果单考虑颜色信息，红框内的像素关系最大，
如何表征这样的关系就是一个问题。很遗憾，我们不能事先提取出这样的区域
，因为图像分割真的很耗时，并且不稳定，这就是作者的牛逼之处，
他想到了MST可以表示这种像素关系，
于是采用像素之间颜色信息作为“边权值”，进一步构建MST。

MST指的是最小生成数，全称是最小权重生成树。
它以全图的像素作为节点，构建过程中不断删除权值较大的边。
注意，是全图所有的像素，然后采用kruskal（克鲁斯卡尔）算法或prim（普里姆）算法进行计算。
这样便得到了全图像素之间的关系。
然后基于这层关系，构建代价聚合，这便是文章标题Non-Local Cost Aggregation的由来。

3. ST（Segment-Tree，分割树，图论分割树）

代码

论文

ST（segment tree）确实是基于NLCA的改进版本，
本文的算法思想是：
    基于图像分割，
    采用和NLCA同样的方法对每个分割求取子树，
    然后根据贪心算法，将各个分割对应的子树进行合并，
    算法核心是其复杂的合并流程。
但是这个分割不是简单的图像分割，其还是利用了最小生成树（MST）的思想，
对图像进行处理，在分割完毕的同时，每个分割的MST树结构也就出来了。
然后将每个子树视为一个个节点，在节点的基础上继续做一个MST，
因此作者号称ST是 分层MST，还是比较贴切的！

算法是基于NLCA的，那么ST和NLCA比较起来好在哪里？
作者给出的解释是，NLCA只在一张图上面做一个MST，
并且edge的权重只是简单的灰度差的衍生值，这点不够科学，
比如说，当遇到纹理丰富的区域时，这种区域会导致MST的构造出现错误
，其实想想看的确是这样，如果MST构造的不好，自然会导致视差值估计不准确。
而ST考虑了一个分层的MST，有点“由粗到精”的意思在里面。

ST是NLCA的扩展，是一种非传统的全局算法，
与NLCA唯一的区别就在于ST在创建MST的时候，引入了一个判断条件，使其可以考虑到图像的区域信息。
这点很新颖，说明作者阅读了大量的文章，并且组合能力惊人，组合了MST和基于图表示的图像分割方法。
它的运行时间虽然比NLCA要大一些，但是相比较全局算法，速度已经很可以了。
但是ST也有一些缺陷，首先，算法对图像区域信息的考虑并不是很严谨，
对整幅图像用一个相同的判断条件进行分割，分割效果不会好到哪里去，
并且基于实际数据实测，会发现视差图总是出现“白洞”，说明该处的视差值取最大，
这也是区域信息引入的不好导致的。虽然在细节上略胜于NLCA，但是算法耗时也有所增加。
上述原因也是本文引用率不佳的原因。

4.上下采样 视差精细化

上下采样

upsampling的意思是上采样，是图像方面的概念，之所以要用NL作上采样，主要原因还是速度问题，
往往stereo mathcing方向的算法的时间复杂度都比较高，于是为了提高速度，
考虑在原图像的下采样图像计算视差图，然后在对低分辨率的视差图进行上采样成为高分辨率的视差图，
这是一个折中的方法，效果肯定没有直接在高分辨率图像上生成视差图好，但是速度却能够提高几倍不止。

一般的上采样方法相信大家都比较熟悉，最基本的思想就是根据当前像素邻域内的像素值进行估计，比
如说权值滤波，也有的文献是基于3Dtof相机获得低分辨率视差图和高分辨率的彩色图，然后在进行上采样操作。
这篇文献就是基于权值滤波的思想，将NL应用在了视差图上采样方向，其流程图如下所示： 

原图像——————————>下采样————————>计算视差图—————|
     |                                       |
     |________-> 计算最小生成树————————————————>根据 最小生成树 进行上采样

texture handing

texture handing一般翻译成为纹理抑制或者是纹理处理，指的是对于具有复杂的纹理区域
，一般要在边缘保持的同时模糊区域内的纹理，这是一个图像处理上经常用的方法，
作者在这上面也下了功夫，目的还是估计视差图，因为NLCA算法对于带噪声图像效果很差，
尤其是在其纹理丰富区域，所以催生了这一块应用。

视差图求精 refinement

视差图求精是重头戏，由于遮挡，光照等原因，求出来的视差图往往部分点视差不正确，
需要对视差图重新求精，是stereo matching必不可少的一步，NL同样在这里有应用，
它事先利用left-right-check对左右视差图进行处理，得到视差图的稳定点和不稳定点，
同时直接在左视差图上定义新的代价值，再同样利用原图所得的MST，
对所有像素点重新进行代价聚合，最后利用”胜者为王”算法估计新的视差。

5. DoubleBP 分层 Belief Propagation 置信度传播算法 由粗到精的思想 全局立体匹配算法的代表性作品

论文

参考

DoubleBP是一个立体匹配全局算法，
来自于论文《Stereo Matching with Color-Weighted Correlation, Hierarchical Belief Propagation, and Occlusion Handling》
DoubleBP共有两大贡献，一个是考虑到了图像的稳定点与非稳定点，
然后根据低纹理区域和遮挡区域内的非稳定点来不断的更新能量函数中的数据项，
最终使得视差能够正确地从稳定点传播到非稳定点（这点和tree filter那篇博客很像哦）。
另一个就是融合了当前在立体匹配领域中几个不错的方法。所言不虚，因为在DoubleBP之前，
所有的全局算法都没有考虑在稳定点上做文章，其实我们想想看，
稳定点肯定靠谱一些，放弃不稳定点直觉上是正确的。

DoubleBP是绝对的全局算法，其重点放在了视差图的迭代求精上，
靠的就是不断更新能量函数，然后利用HBP不断的求解。全局算法耗时严重，
作者故意在设计算法的时候，使之更加适应并行计算。
这样也具有一定的实际应用能力，但是很可惜，就算在FPGA上并行计算，仍旧达不到实时。

结论

算法后续采用了“亚像素求精+均值滤波”的办法进一步提升了效果，我们会发现对于低纹理区域的黑色斑块，
通过亚像素求精竟然全部消失，其实每个算法中都可以利用这种方法进行后处理，
但是我在其他算法中得不到太明显的效果，远低于文本的提升，想来想去可能是由于经过迭代求精之后，
DoubleBP得到的像素代价序列更加靠谱，这样求取的局部极值自然就更加精确，反之，
如果求得的代价序列并不理想，那么经过二次多项式拟合之后，求取的极值可能会起到相反的作用。
当然这只是我的实验效果的猜想，还请大家指教。

这是一篇很牛的文章，应该可以被称为全局立体匹配算法的代表性作品，用工程组合的方法，
将多个模块组合起来，达到精确的估计效果，引用率很高，我看完这篇文章之后，
最大的感觉就是在立体匹配这个领域，复杂的“一步到位”的方法，可能并不适用，
还是工程组合的方法适合这个领域，这篇文章提出的像素分类，视差值从稳定点传递到不稳定点的思想，
被多篇论文所采用，难怪作者认为这才是他最大的贡献。

6. 置信度传播算法（Belief-Propagation）与立体匹配

参考

置信度传播算法（Belief-Propagation）在立体匹配。
现有的全局立体匹配算法，很大一部分都是基于Belief-Propagation来进行视差求精，
二者天然的纽带就是，一幅图加上对应像素标签就可以看成是一个马尔科夫场，
只要有马尔科夫场，很自然地就可以利用BP算法进行优化求解。
马尔科夫场是一种概率图模型，图中的节点就是像素，图中的隐节点就是标签，
在Stereo-Matching里面，标签就是像素的视差值，视差值总是会有一个范围，
BP就是在这个自定义空间中找到使得全局能量最小的那些视差值。


一般的非全局算法，在  代价聚合值 求出来之后便戛然而止，
直接来一个WTA（赢者通吃），就算是把视差求出来了，如果代价聚合准确还可以，
如果不准，求出来的视差图“惨不忍睹”，
全局算法就是在代价聚合的基础上加了一个双保险，
不单单希望代价聚合值的和最小化，
还要考虑图像的区域性，
桌面肯定是一个区域，
一个人肯定是一个区域等等等等，
它们的视差应该差不多，
所以直接利用这个数学模型来达到这种需求。

立体匹配要解决的主要问题有两个，
    一个是低纹理区域的视差估计，
    一个是深度不连续区域的视差估计，也就是遮挡区域，
作者认为深度不连续区域往往就是颜色不连续区域（这点多篇论文都这样提到过，SegmenTree，DoubleBP等等）。
而BP有两大优点，
   第一个是信息不对称，
   第二是BP的消息值是自适应的，
第一点我也没有彻底弄明白原理，关于第二点，BP往往在低纹理区域中能够将消息传递到很远，
但在深度不连续区域却马上就会停止传递，所以说它是自适应的。

7. Spatial-Depth Super Resolution for Range Images 对深度图进行上采样

论文

Range Images 它的意思就是深度图像，并且特指通过深度相机（例如，TOF相机）采集到的深度图像。
给定一个低分辨率视差图，通过本文提出的算法，将低分辨率视差图上采样成为高分辨率视差图。
为什么要将低分辨率深度图上采样为高分辨率深度图，原因其实很简单，就是为了一个速度。
想得到高精度的视差图依赖于复杂的全局算法，非常耗时，距离实时应用还有很大的距离，
于是作者另辟蹊径，直接通过对低分辨率深度图上采样，达到精度还不错的高分辨率视差图，这是一个具有开创性的想法。

算法思想

本文的算法思想可以用一句话概括：结合硬件采集的低分辨率视差图以及高分辨率原图，
利用双边滤波对低分辨率视差图进行上采样，得到与原图同等分辨率的视差图。

步骤：
1). 我们先对低分辨率视差图进行上采样，当然，这样的视差图一定很挫。

2). 我们再根据上采样得到的大视差图，计算代价体(cost volume)，其实就是代价计算项（参考DoubleBP）。

3). 根据得到的cost volum，利用双边滤波对其进行处理，得到更好的cost volum。

4). 基于更好的cost volum，用WTA（牛逼哄哄的胜者为王算法），得到视差图。

5). 还没完，对得到的视差图进行亚像素求精。

6). 尽情的迭代，到爽为止！！！

双边滤波

滤波算法中，目标点上的像素值通常是由其周围的一个局部区域中的像素所决定，
例如可以基于像素之间的灰度值或位置关系。
图像的滤波算法有很多种，高斯滤波，gabor滤波等等，
每种都有自己的特点，例如最简单的高斯滤波，其只考虑了图像的空间位置信息，
根据像素与中心像素的距离远近，计算像素的权值，高斯滤波对图像所有区域都“同等对待”，
模糊了纹理的同时也模糊了边缘。而双边滤波却不是这样，
它不仅考虑到了像素之间的位置关系，还考虑到了像素之间的颜色差异，

这样就使得双边滤波是一种“边缘保持（Edge-Preserving）”的滤波方法，

仅对非边缘区域进行较大程度的模糊，针对边缘由于考虑到了像素之间的颜色的差异，
和边缘颜色相近的像素能够得到较大的权值，和边缘颜色不相似的像素只能够获得较小的权值，
自然使得边缘一侧的像素权值较小，对边缘的干扰作用也随之减弱。
滤波之后，边缘的颜色还是之前的颜色，只有微微的模糊。

亚像素求精

但是本文的重点不是这里，重点在求出视差值之后的“亚像素求精”，
大部分的立体匹配算法都可以进行亚像素求精，
至于为什么要进行亚像素求精？
那是由于整数级别的视差值计算出来的深度值不会精确到哪里去（用公式算算就知道了，如果基线距离过大），
如果我们想求取精确的深度信息，那么亚像素求精是最简单有效的方法。

本文采用的方法就是传统的 二次多项式插值，这里很有意思。
    因为我们得到的视差值都是离散的，并且是整数，举个例子，
    如果我们通过WTA得到一点的视差值是10，以及对应的代价值30，
    我们同时也可以得到视差9的代价值（假设是40），
    视差11的代价值（假设为50），
    我们可以利用二次多项式函数（如下所示）来计算浮点型的视差值.
    
    f(x)=a*x^2 + b*x + c
    xmin = -b/2a
    参数有a,b,c共三个，所以我们要想求解这三个参数，就需要3个方程，
    根据上面的（10, 30）、（9, 40）、（11, 50），我们就可以求解出这个多项式的最小值，
    这个最小值就是所谓的 多项式差值，最小值的公式如下：
    
    xmin = d - ( ( f(d+) - f(d-) ) / ( 2 * (f(d+) + f(d-) - 2*f(d) ) ) )
    d=10  ; f(d) = 30
    d+ = 11 ; f(d+) = 50
    d- = 9  ; f(d-) = 40
    这就是亚像素求精的全部内容，这样的方法可以应用在任何一种立体匹配算法上，
    非常通用，我认为这一步是非常重要的，尤其在我们要基于视差图进行进一步分析的时候，
    整形的数据往往误差太大，果断弄成浮点型的数据。文中称为离散和连续，一个意思。
    
    在计算完每个像素点的亚像素之后，通常还要进行均值滤波，在9*9的窗口中。

8. AD-Census，作者与SegmentTree是同一人

论文 On Building an Accurate Stereo Matching System on Graphics Hardware

参考

特点：
    1. 适合并行；
    2. 基于特征融合的代价计算；
    3. 基于自适应区域的代价聚合；

1. 适合并行

这点是相当吸引人的，也是作者的出发点，众所周知，全局算法不适合并行，为啥？
因为建立了复杂而且漂亮的能量函数，需要用同样复杂而且漂亮的迭代优化算法求解，
可惜的是这样的优化算法如果想并行处理难度太高，并且也快不到哪里去，
所以导致现有很多全局算法无法得到应用，我们只能眼睁睁的看着middlebery上的顶级算法
，一边淌着哈喇子，一边望洋兴叹。不过本文关于并行这块的解释就不多说了，
不亲自动手实现是无法体会出来并行带来的快感。

2. 特征融合 代价计算(cost initialization)：绝对差AD+Census变换算法

我看过的文献中，很少有在代价计算这一步中融合多种特征的，
一般只采用一种特征而已并且对这块内容的研究也偏少，作者另辟蹊径的融合了现有特征AD和Census，
AD就是最普通的颜色差的绝对值，立体匹配算法中经常使用，
其公式如下所示：
AD：绝对差值，三通道像素绝对差值均值。
reference image一般翻译成为参考图像，
base image和guidance image就是reference image， 一般被翻译成为基准图像，
match image一般被翻译成为匹配图像，那么参考图像和匹配图像的关系是什么呢？
我真的好想说，不就是一个代表左图一个代表右图嘛！

立体匹配的流程，
    a. 左图和右图先做代价计算，怎么做的呢，
        遍历左图中的每一个像素，
        然后根据 视差范围 中的每一个视差值，
        来找到对应 右图的像素，
        然后 根据 公式计算 代价，
    b. 然后再针对左图，遍历每个像素进行代价聚合计算，这就是重点，如
        果你在左图上计算代价聚合，那么左图就叫做参考图像，右图就是匹配图像，反之，反过来叫。

Census 代价 与 AD 代价融合

代码

Census指的是一种代价计算方法，其属于非参数代价计算方法中的一种（另外一个代表是rank transform），
准确的说它是一种距离度量，它的计算过程的前半部很像经典的纹理特征LBP，
就是在给定的窗口内，比较中心像素与周围邻居像素之间的大小关系，
大了就为1，小了就为0，然后每个像素都对应一个二值编码序列，
然后通过 汉明距离(类似字符串编辑距离)来表示两个像素的相似程度。

Census保留周边像素空间信息，对光照变化有一定鲁棒性。
Census具有灰度不变的特性，所谓灰度不变指的就是像素灰度值的具体大小和编码之间的相关性不是很强，
它只关心像素之间的大小关系，即使你从5变成了10，但只要中心像素是15，就一点事情都木有，
这样的性质我们肯定会想到它一定对噪声和鲁棒，的确是这样。
但是它的缺点也很明显，按照文章的说法， 对于结构重复的区域这个特征就不行了，那基于颜色的特征AD呢？
它是对颜色值很敏感的，一旦区域内颜色相近（低纹理）或者有噪声那么挂的妥妥的，
但是对重复结构却不会这样，基于这种互补的可能性，作者尝试将二者进行融合，
这是一种很简单的线性融合但是却取得了很好的效果：
f(cost,参数) = 1 - exp(- cost/参数)； 画归到 0~1， 之后再相加。

两种计算方法得到的取值范围可能会相差很大，比如一个取值1000，
另一个可能只取值10，这样便有必要将两者都归一化到[0，1]区间，
这样计算出来的C更加有说服力，这是一种常用的手段。
论文中给出了AD，Census，AD-Census对一些细节处理的效果图，
可以看得出来各自的优缺点，第一行是重复纹理区域，
第二行是低纹理区域，白色与黑色都说明计算的结果很差。

AD往往比Census在物体边缘上的处理更好一些，边缘明显清晰，但是AD得到的噪声太多，并且在低纹理区域，
AD出现了很大的空洞，在这一点上Census做的相对较好，
AD-Census在物体边缘上的效果是二者的折中，但噪声更少，整体效果更加理想。

// 对应像素差的绝对值 3通道均值  Absolute Differences
float ADCensusCV::ad(int wL, int hL, int wR, int hR) const
{
    float dist = 0;
    const Vec3b &colorLP = leftImage.at<Vec3b>(hL, wL);// 左图对应点 rgb三色
    const Vec3b &colorRP = rightImage.at<Vec3b>(hR, wR);// 右图对应点 rgb三色

    for(uchar color = 0; color < 3; ++color)
    {
        dist += std::abs(colorLP[color] - colorRP[color]);// 三色差值 求和
    }
    return (dist / 3);//3通道均值
}

// census值
float ADCensusCV::census(int wL, int hL, int wR, int hR) const
{
    float dist = 0;
    const Vec3b &colorRefL = leftImage.at<Vec3b>(hL, wL); // 左图 中心点 RGB颜色
    const Vec3b &colorRefR = rightImage.at<Vec3b>(hR, wR);// 右图 中心点 RGB颜色

    for(int h = -censusWin.height / 2; h <= censusWin.height / 2; ++h)// 窗口 高
    {
        for(int w = -censusWin.width / 2; w <= censusWin.width / 2; ++w) // 窗口 宽
        {// 在指定窗口内比较周围亮度值与中心点的大小
            const Vec3b &colorLP = leftImage.at<Vec3b>(hL + h, wL + w);  // 左图 窗口内的点
            const Vec3b &colorRP = rightImage.at<Vec3b>(hR + h, wR + w); // 右图 窗口内的点
            for(uchar color = 0; color < 3; ++color)
            {
      // bool diff = (colorLP[color] < colorRefL[color]) ^ (colorRP[color] < colorRefR[color]);
      // 左右图与中心点的大小比较 (0/1)，都比中心点小/都比中心点大 乘积就大于0
      // 一个小，一个大乘积就小于0
         bool diff = (colorLP[color] - colorRefL[color]) * (colorRP[color] - colorRefR[color]) < 0;
          // 记录比较关系也不一致的情况
         dist += (diff)? 1: 0;// 匹配距离用汉明距表示 
// 都比中心点大/小　保留周边像素空间信息，对光照变化有一定鲁棒性
            }
        }
    }

    return dist;
}
// ad + census值 信息结合
float ADCensusCV::adCensus(int wL, int hL, int wR, int hR) const
{
    float dist;

    // compute Absolute Difference cost
    float cAD = ad(wL, hL, wR, hR);

    // compute Census cost
    float cCensus = census(wL, hL, wR, hR);

    // 两个代价指数信息结合 combine the two costs
    dist = 1 - exp(-cAD / lambdaAD); // 指数映射到0~1
    dist += 1 - exp(-cCensus / lambdaCensus);

    return dist;
}

但传统Ｃｅｎｓｕｓ变换所获得的像素间关系是基于灰度值的比较，故而Ｃｅｎｓｕｓ变换结果 
仍然受光照等外界因素影响［４＾６］。尚可可等实验研究发现ＨＳＶ色彩空间中，将（Ｓ＋Ｖ）／Ｈ 
作为一个新的参量，该参量对光照等因素具有较好的鲁棒性。因此，本文将巧＋Ｖ）／Ｈ引入 
Ｃｅｎｓｕｓ变换中代替原有的像素灰度值，可有效降低光照等外界环境的影响。 

3. 自适应区域代价聚合 aggregation 代价聚合(cost aggregation) 动态十字交叉域

一般的代价聚合思想：
    局部算法采用一个固定或者自适应窗口来代价聚合；
        一个领域内的代价合并（聚合相当于代价滤波）
        BF（bilateral filter，双边滤波器 ），双边滤波器就是对窗口内像素进行距离加权和亮度加权。
        GF（guided image filter，引导滤波器），基于滤波器的方法是设定一个窗口，在窗口内进行代价聚合。
   全局算法采用整幅图像得到的抽象结构来代价聚合，
        例如MST((minimum spanning tree最小生成树)、ST(分割树)马尔科夫图模型等等。
        
就是事先确定一个有意义的区域，之后直接在这个区域内进行代价聚合。

ADCensus建立了一个灰常有意思的，工程化的区域结构，分割算法耗时不舍得用，干
脆我直接用相对暴力的方案对图像进行分割好了，
看图说话，下图就是作者采用的分割方法。

构建动态交叉域：

采用方法的思想很简单，
当前像素假设是p（水平和垂直十字区域），我对p先进行垂直方向的遍历，
如果像素q满足两个约束，那么就算同一分割区域，否则遍历停止，
然后再在得到的N个q和p的水平方向根据同样的规则进行遍历，于是就得到了对应的分割区域。
然而，作者从来都没有说对图像进行了分割，只是说确定p的cross，其实就是分割的意思。
约束如下所示，这个约束是经过改造过的（
cross region不是作者提出来的，也是引用他人的方法，作者对约束从两个扩充为三个），
这么改的原因是作者考虑到了之前的约束方案会导致将边缘点也包括进去，
这样会对边缘的视差计算十分不利，于是提出了一个更加严格的约束形式，
考虑到了相邻像素色彩上的差异。

水平上临近点的所有竖直临近点（或者称arms）所覆盖的区域，
与反过来的先竖直后水平所覆盖的区域本就是两回事，不是一定会相同的。

计算每个像素的上下左右边界，在进行代价聚合时，若采用先水平后垂直的方式，
就是对边界内垂直线上的每个像素的水平边界先加和，
然后再把中心点像素垂直线上的像素进行加和？


代价聚合的目的：减少初始代价中的匹配模糊和图像噪声的影响。
代价聚合的依据：相似的区域具有相似的视差；
常见代价聚合方法：图像分割，自适应权重，自适应窗口等。
这篇文章采用动态交叉域的代价聚合方法：
分为两步：交叉域构建，代价聚合；
代价聚合规则：计算颜色差值和空间距离，通过3规则构建交叉域；通过4次迭代进行代价聚合。
优点：对大的少纹理和视差不连续区域减少匹配误差。

代价聚合：

迭代4次的正确理解为：对所有像素点水平边界计算一次cost累加（1次完成）；
对所有像素点垂直边界计算cost累加一次（2次完成）;
对所有像素点垂直边界计算cost累加一次（3次完成）；
对所有像素点水平边界计算一次cost累加（4次完成）。 
发现两次cross-based region 形状是不一样的。
所以为什么改变聚合方向顺序会有不一样的结果。

3. 视差优化(disparity computation)：扫描线视差优化 ScanlineOptimization

目的：选择最佳的视差范围，生成视差图。
4方向的扫描线优化策略：适合并行计算，减少匹配模糊。

Scanline方法文章改进的是smi-global matching的能量函数求解方法，
只是将原来的8个方向减少到4个方向，重新看下SGM原理便不难理解，
SGM能量函数在二维图像中寻找最优解采用了分而治之的方法，
分为8或4个一维问题。下面分析下从左到右方向的一维动态规划问题。

每一个点的代价聚合值是“当前代价 + 
min（路径相邻点的当前视差代价聚合值，
路径相邻点的视差差值为1的代价聚合值 + P1，
路径相邻点的视差插值大于1的最小代价聚合值 + P2）- 路径相邻点的视差插值大于1的最小代价聚合值 ”，
听起来够绕口的，其实就好比最小代价的蔓延，
当前代价聚合值由当前代价和路径上一点的加了惩罚的最小代价聚合值所决定（
最后那一项纯粹是为了防止数字过大，这是常用手段）.

r指某个指向当前像素p的方向，在此可以理解为像素p左边的相邻像素。

Lr(p, d) 表示沿着当前方向（即从左向右），当目前像素p的disparity取值为d时，其最小cost值。

这个最小值是从4种可能的候选值中选取的最小值：
    1.前一个像素（左相邻像素）disparity取值为d时，其最小的cost值。
    2.前一个像素（左相邻像素）disparity取值为d-1时，其最小的cost值+惩罚系数P1。
    3.前一个像素（左相邻像素）disparity取值为d+1时，其最小的cost值+惩罚系数P1。
    4.前一个像素（左相邻像素）disparity取值为其他时，其最小的cost值+惩罚系数P2。
另外，当前像素p的cost值还需要减去前一个像素取不同disparity值时最小的cost。
这是因为Lr(p, d)是会随着当前像素的右移不停增长的，为了防止数值溢出，所以要让它维持在一个较小的数值。

4. 后处理(refinement)：多步后处理操作 Multi-stepDisparity Refinement 多步视差细化

a. 离群点检测：通过左右一致性准则，检测出离群点：遮挡区域和视差不连续区域的点

   条件的异常点被分为遮挡点和误匹配点，其中对于异常点p的左视差Disp(p)，
   如果极线范围内右Disp(p)被check则该点定义为误匹配点，否则该点为遮挡点。

b. 传播异常视差点, Iterative Region Voting 迭代区域投票法
   它的目的是对outlier进行填充处理，一般来说outlier遮挡点居多，
   填充最常用的方法就是用附近的稳定点就行了，省时省力，就是不利于并行处理，
   作者要设计的是一个完全适合GPU编程的算法，所以采用了迭代区域投票法，
   具体做法是对之前区域构建所得到的每个区域求取视差直方图（不要归一化），
   例如，得到的直方图共有15个bin，最大的bin值是8，那么outlier的视差就由这个8来决定，
   但是稳定点的个数必须得比较多，比较多才有统计稳定性.

   这里再次用到cross-based自适应窗口，对于异常视差点p，统计窗口内所有有效视差点构成直方图Hp，如果满足下面条件

   此外，这个方法是迭代的，这只是针对稳定点个数具有统计意义的区域，
   有些outlier由于区域内稳定点个数不满足公式，这样的区域用此方法是处理不来的，
   只能进一步通过16方向极线插值来进一步填充，
   二者配合起来能够取得不错的效果，自己做了实验，这两种方法的顺序也必须一先一后，否则效果也不行，
   说明一个是大迂回战略，目的是消灭有生力量，
   一个是歼灭战，打的是漏网之鱼，二者珠联璧合，可喜可贺。
    
    
c. 异常点修复 Proper Interpolation:
    根据异常点分类采取不同的修复方式
    大体可以理解为对于遮挡点，该点来自背景的可能性比较大，
    采用周围16点相邻点视差最小值进行填充；
    否则采用相邻颜色相似度最高点的视差值进行填充。
    
d. 非连续视差调整 Depth Discontinuity Adjustment:
    非连续视差适应，先求下边缘检测，对于视差值在边缘上的点p找到边缘两侧点p1, p2，
    该点视差 Dl(p)取这两个侧点中代价最小的那个视差值。
    该方法可以减少非连续性错误。
e. Sub-pixel Enhancement: 亚像素增强
    二次线性插值

f. 常规中值滤波
    
作者也采用left-right-check的方法将像素点分类成为三种：
遮挡点，非稳定点，稳定点。
对于遮挡点和非稳定点，只能基于稳定点的视差传播来解决，本文在视差传播这一块采用了两种方法，
一个是迭代区域投票法，
另一个是16方向极线插值法，
后者具体来说：沿着点p的16个方向开始搜索，如果p是遮挡点，
那么遇到的第一个稳定点的视差就是p的视差，如果p是非稳定点，
那么遇到第一个与p点颜色相近的稳定点的视差作为p的视差。
针对于视差图的边缘，作者直接提取两侧的像素的代价，
如果有一个代价比较小，那么就采用这个点的视差值作为边缘点的视差值，
至于边缘点是如何检测出来的，很简单，对视差图随便应用于一个边缘检测算法即可。
做完这些之后，别忘记亚像素求精，这和WTA一样，是必不可少的。
流程图如下，忘记说了，再来一个中值滤波吧，因为大家都这么玩，属于后处理潜规则。

9. Semi-Global Matching（SGM）半全局匹配

参考

代码

论文：Stereo Processing by Semi-Global Matching and Mutual Information

SGM中文名称“半全局匹配”，顾名思义，其介于局部算法和全局算法之间，
所谓半全局指的是算法既没有只考虑像素的局部区域，也没有考虑所有的像素点。
例如，BM计算某一点视差的时候，往往根据目标像素周围的矩形区域进行代价聚合计算；
DoubleBP在计算目的像素视差的时候，考虑的则是图像所有的像素点。
抛开具体的方法不说，SGM中考虑到的只有非遮挡点，这正是定义为半全局的原因。

论文关键点：
    分层互信息的代价计算+
    基于动态规划的代价聚合+
    其他

a. 代价计算 互信息 Mutual Information

它采用了基于互信息的计算方法，互信息是一种熵。
那我们就先说说熵，熵是用来表征随机变量的不确定性（可以理解为变量的信息量），
不确定性越强那么熵的值越大（最大为1），那么图像的熵其实就代表图像的信息量。
互信息度量的是两个随机变量之间的相关性，相关性越大，那么互信息就越大。
可以想想看，两幅图像如果匹配程度非常高，说明这两幅图像相关性大还是小？
显然是大，知道一幅图像，另外一幅图像马上就知道了，相关性已经不能再大了！！！
反之，如果两幅图像配准程度很低，那么两幅图像的互信息就会非常小。
所以，立体匹配的目的当然就是互信息最大化。
这就是为什么使用互信息的原因。

熵和互信息的定义分别如下所示：
熵：E = sum(pi * log(pi))  pi为图像分布的概率，即图像的灰度直方图(像素数/像素总数)
交叉熵（衡量p与q的相似性）： sum(pi * log(qi)) pi、qi 0~255两幅图像的直方图概率
联合熵（（X,Y）在一起时的不确定性度量）： sum(pij * log(pij))

图像的灰度值是0~255，每个灰度值对应的像素个数除以图像像素个数就是该灰度值对应的概率，
单幅图像的概率密度是一维的，那么自然地，
两幅图像的 联合概率密度就是二维的，它的定义域取值就是（0，0）~（255，255）

互信息对光照具有鲁棒性，
我们已经得到了互信息图，剩下要做的事情只是根据左图和右图挑选出来的像素点的灰度值对，
在互信息图中直接查找就行（又是一个速度优势），
注意：要取个负号，这点直觉上很好理解，
互信息越大->相关性越大->两个点的匹配程度越高->代价计算值理应越小。

Visual Correspondence Using Energy Minimization and Mutual Information

b.

利用动态规划来求解E，其实这个求解问题是NP完全问题，
想在2D图像上直接利用动态规划求解是不可能的，只有沿着每一行或者每一列求解才能够满足多项式时间（又叫做扫描线优化），
但是这里问题来了，如果我们只沿着每一行求解，那么行间的约束完全考虑不到，
q是p的领域的点其实这个时候被弱化到了q是p的左侧点或者右侧点，这样的求优效果肯定很差。
于是，大招来了！！我们索性不要只沿着横或者纵来进行优化，而是沿着一圈8个或者16个方向进行优化。

smi-global matching的能量函数求解方法，
只是将原来的8个方向减少到4个方向，重新看下SGM原理便不难理解，
SGM能量函数在二维图像中寻找最优解采用了分而治之的方法，
分为8或4个一维问题。下面分析下从左到右方向的一维动态规划问题。

每一个点的代价聚合值是“当前代价 + 
min（路径相邻点的当前视差代价聚合值，
路径相邻点的视差差值为1的代价聚合值 + P1，
路径相邻点的视差插值大于1的最小代价聚合值 + P2）- 路径相邻点的视差插值大于1的最小代价聚合值 ”，
听起来够绕口的，其实就好比最小代价的蔓延，
当前代价聚合值由当前代价和路径上一点的加了惩罚的最小代价聚合值所决定（
最后那一项纯粹是为了防止数字过大，这是常用手段）.

r指某个指向当前像素p的方向，在此可以理解为像素p左边的相邻像素。

Lr(p, d) 表示沿着当前方向（即从左向右），当目前像素p的disparity取值为d时，其最小cost值。

这个最小值是从4种可能的候选值中选取的最小值：
    1.前一个像素（左相邻像素）disparity取值为d时，其最小的cost值。
    2.前一个像素（左相邻像素）disparity取值为d-1时，其最小的cost值+惩罚系数P1。
    3.前一个像素（左相邻像素）disparity取值为d+1时，其最小的cost值+惩罚系数P1。
    4.前一个像素（左相邻像素）disparity取值为其他时，其最小的cost值+惩罚系数P2。
另外，当前像素p的cost值还需要减去前一个像素取不同disparity值时最小的cost。
这是因为Lr(p, d)是会随着当前像素的右移不停增长的，为了防止数值溢出，所以要让它维持在一个较小的数值。