菜菜的机器学习sklearn实战-----sklearn中的降维算法PCA和SVD

菜菜的机器学习sklearn实战-----sklearn中的降维算法PCA和SVD

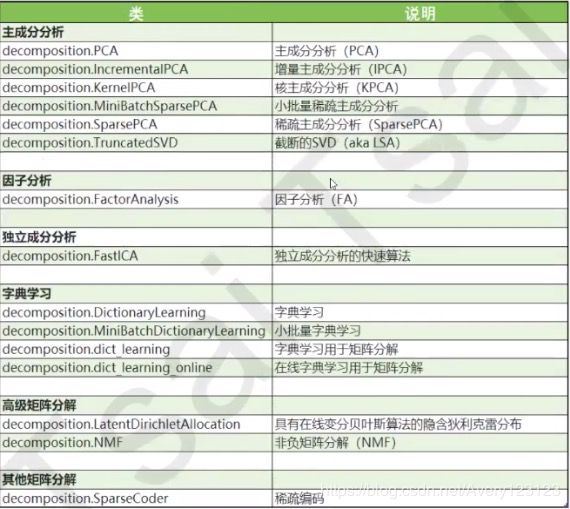
概述

从什么叫维度说开来

简单讲，shape中返回了几个数字就是几维。

一张表最多就是一维
当一个数组中存在2张3行4列的表时，shape返回的是（更高维，行，列）
当数组中存在2组2张3行4列的表时，数据就是4维，shape返回（2，2，3，4）

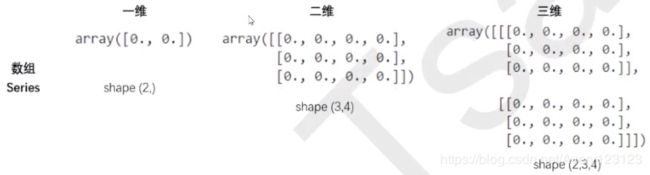
数组中的每一张表，都是一个特征矩阵或者一个DataFrame，这些结构永远只有一张表，所以一定要有行列，其中行是样本，列是样本特征。

针对每一张表，维度指的是样本的数量或者特征的数量，一般无特别说明，指的都是特征的数量。
除了索引之外，一个特征是一维，两个特征是二维，n个特征是n维。

对于图像来说，维度就是图像中的特征向量的数量（坐标轴的 个数）

降维算法中的“降维”，指的就是降低特征矩阵中特征的数量

降维的目的：
就是让算法运算更快，效果更好
另外的一个应用就是：数据可视化

sklearn中的降维算法

PCA与SVD

我们希望减少特征的数量，又保留大部分有效信息

在降维中，PCA使用的信息衡量指标，就是样本方差，又称可解释性方差。方差越大，特征所带的信息量越多。

降维究竟是如何实现的

PCA作为矩阵分解算法的核心算法

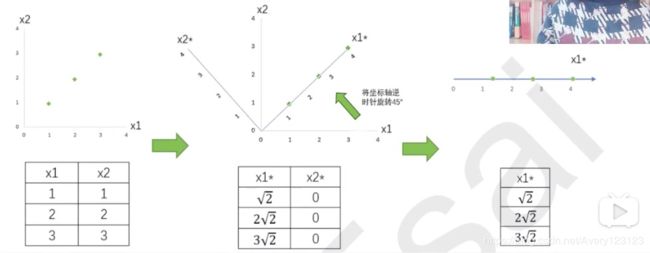
降维过程中的几个重要步骤：

二维特征矩阵	n维特征矩阵
输入原数据，结构为（3,2）找出样本的2个特征对应的直角坐标系，本质是找出这2个特征构成的2维平面	输入原数据，结构为（m,n）找出原本的n个特征向量构成的n维空间V
决定降维后的特征数量：1	决定降维后的特征数量：k
旋转，找出一个新坐标系本质是找出2个新的特征向量，以及它们构成的新2维平面	决定降维后的特征数量：k
找出数据点在新坐标系上，2个新坐标轴上的坐标	找出原始数据在新特征空间V中的n个新特征向量上对应的值，“将数据映射到新的空间中”
选取第1个方差最大的特征向量，删除没有被选中的特征，成功将2维平面降为1维	选取前K个信息量最大的特征，删掉没有被选中的特征，成功将n维空间V降为k维

找出n个新特征向量，让数据能够被压缩到少数特征上并且总信息量不损失太多的就是矩阵分解

思考：PCA和特征选择技术都是特征工程的一部分，他们有什么不同？
特征选择具有可解释性

而PCA，在新的特征矩阵生成之前，我们无法知晓PCA都建立了怎样的新特征向量，新特征矩阵生成之后也不具有可读性

因此，PCA一般不适用于探索特征与标签之间关系的模型（如线性回归），因为无法解释的新特征和标签之间的关系不具有意义。在线性回归模型中，我们使用特征选择。

重要参数n_commpenents

n_components是我们降维后需要的降维，即降维后需要保留的特征数量。

迷你案例：高维数据的可视化

import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA

iris = load_iris()
y = iris.target
y
X = iris.data
X

#调用PCA
pca = PCA(n_components=2)
pca = pca.fit(X)
X_dr = pca.transform(X)
X_dr

#fit_transform一步到位
#X_dr = PCA(2).fit_transform(X)

#可视化
#要将三种鸢尾花的数据显示二维平面坐标系中，对应的两种的两个坐标（两个特征向量）应该是三种鸢尾花降维后的X1和X2，怎样才能取出三种鸢尾花下不同的x1和x2
X_dr[y==0,0]#这里是布尔索引----0表示是第0种标签的第1列
#要展示三中分类的分布，需要对三种鸢尾花分别绘图
#可以写成三行代码，也可以写成for循环

plt.figure()
plt.scatter(X_dr[y==0,0],X_dr[y==0,1],c="red",label=iris.target_names[0])
plt.scatter(X_dr[y==1,0],X_dr[y==1,1],c="black",label=iris.target_names[1])
plt.scatter(X_dr[y==2,0],X_dr[y==2,1],c="orange",label=iris.target_names[2])
plt.legend()
plt.title('pca of IRIS dataset')
plt.show()

colors = ['red','black','orange']
iris.target_names
plt.figure()
for i in [0,1,2]:
    plt.scatter(X_dr[y==i,0]
               ,X_dr[y==i,1]
               ,alpha=.7
               ,c=colors[i]
               ,label=iris.target_names[i]
               )
plt.legend()
plt.title('PCA of IRIS dataset')
plt.show()

探索降维后的数据

#属性explained_variance,查看降维后每个新特征向量上所带的信息量大小（可解释性方差的方法）
pca.explained_variance_

#属性explained_variance_ratio查看降维后每个特征向量所占的信息量占原始数据总量的百分比
pca.explained_variance_ratio_

pca.explained_variance_ratio_.sum()

选择最好的n_components:累积可解释方差贡献率曲线

import numpy as np
pca_line = PCA().fit(X)
plt.plot([1,2,3,4],np.cumsum(pca_line.explained_variance_ratio_))
plt.xticks([1,2,3,4])
plt.xlabel("number of components after dimension reduction")
plt.ylabel("cumulative explained variance")
plt.show()

最大似然估计自选超参数

pca_mle = PCA(n_components="mle")
pca_mle = pca_mle.fit(X)
X_mle = pca_mle.transform(X)

X_mle
#可以发现，mle为我们自动选择了3个特征

pca_mle.explained_variance_ratio_.sum()
#得到了比设定2个特征时更高的信息含量

按信息量占比选超参数

pca_f = PCA(n_components=0.97,svd_solver="full")
pca_f = pca_f.fit(X)
x_f = pca_f.transform(X)
pca_f.explained_variance_ratio_

PCA中的SVD

重要参数svd_solver与random_state

svd_solver的4个选项：
“auto” 通常选用

“full”

“arpack” 适合特征矩阵稀疏

“randomized” 适合特征矩阵巨大，计算量大

重要属性components_

重要接口inverse_transform

将归一化、标准化之后的数据变回去

迷你案例：用人脸识别看PCA降维后的信息保存量

from sklearn.datasets import fetch_lfw_people
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import numpy as np

faces = fetch_lfw_people(min_faces_per_person=60)
X = faces.data
pca = PCA(150)#实例化
X_dr = pca.fit_transform(X)
X_dr.shape
X_inverse = pca.inverse_transform(X_dr)
X_inverse.shape

#可视化
fig,ax = plt.subplots(2,10,figsize=(10,2.5),subplot_kw={"xticks":[],"yticks":[]})

for i in range(10):
    ax[0,i].imshow(faces.images[i,:,:],cmap="binary_r")
    ax[1,i].imshow(X_inverse[i].reshape(62,47),cmap="binary_r")
    

降维不是你完全可逆的

迷你案例：用PCA做噪音过滤

from sklearn.datasets import load_digits
from sklearn.decomposition import PCA
import matplotlib.pylab as plt
import numpy as np

digits = load_digits()
digits.data.shape

def plot_digits(data):
    fig,axes = plt.subplots(4,10,figsize=(10,4)
                           ,subplot_kw = {"xticks":[],"yticks":[]})
    for i,ax in enumerate(axes.flat):
        ax.imshow(data[i].reshape(8,8),cmap="binary")

#可视化
plot_digits(digits.data)

#加入噪声
rng = np.random.RandomState(42)
noisy = rng.normal(digits.data,2)
plot_digits(noisy)


#过滤噪声
pca = PCA(0.5,svd_solver="full").fit(noisy)
X_dr = pca.transform(noisy)
X_dr.shape

without_noise = pca.inverse_transform(X_dr)
plot_digits(without_noise)

重要接口,参数和属性总结

案例：PCA对手写数字数据集的降维