图/树的遍历:深度优先遍历DFS和广度优先遍历BFS详解与java实现
DFS和BFS
- DFS(Depth-First-Search) 深度优先搜索/遍历
- 基本概念
- 图的深度优先遍历示例
- 概述
- 图(邻接矩阵)的DFS实现(栈或递归)
- 树的深度优先遍历示例
- 概述
- 树的DFS实现(栈或递归)
- BFS(Breadth-First-Search) 广度优先搜索/遍历
- 基本概念
- 图的广度优先遍历示例
- 概述
- 图的BFS实现(队列)
- 树的广度优先遍历示例
- 概述
- 树的BFS实现(队列)
给定一个图和其中任意一点顶点v, 从v出发系统地(按照一定规则) 访问图的全部顶点,且使每个顶点仅被 访问一次,这个过程称为 图的遍历。
图的遍历方法有两种:深度优先遍历DFS和广度优先遍历BFS。
简言之,深度优先可理解为一列一列访问,广度优先就是一行一行访问。(本人胡言乱语)
DFS(Depth-First-Search) 深度优先搜索/遍历
基本概念
从图中某个顶点v出发的深度优先搜索过程DFS可以描述为:
- 访问顶点v,并对v做已访问标记。
- 对于每个顶点v,选择下一个遍历点的策略是从v的未访问的邻接点出发,对图作深度优先的遍历。
图中所有顶点,以及在遍历时经过的边(即从已访问的顶点到达未访问的顶点的边,个人理解就是遍历的路径)构成的子图,称为图的深度优先搜索生成树(或生成森林)。
DFS的遍历规则的重点就是沿着顶点的深度方向遍历。顶点的深度方向即它的邻接点方向。
具体来说,给定一个图G =
所谓的“第一个”是指在图的某种存储结构中(邻接矩阵、邻接表),所有邻接点中存储位置最近的、通常指的是下标最小的。
在遍历过程中通常有以下四种情况出现:
- 顶点有多个未访问邻接点,则选择下标最小的即第一个邻接点作为下一个顶点。
- 顶点只有一个未访问邻接点,只有这一个选择作为下一个顶点。
- 顶点的邻接点都已被访问过的情况,此时需回溯已访问过的顶点。
- 图不连通,所有已访问过的顶点都已回溯完了,仍找不出剩余未访问过的顶点,或当前顶点无任何邻接点。此时需从下标0开始检测visited[i],找到目前仍未访问过的顶点Vi,从顶点Vi开始进行新一轮的深度搜索。
回溯: 类似枚举的搜索尝试过程。沿一条路往前走,当走不通时,按原路返回,返回一步再向前走进行尝试,还走不通继续返回。返回一步尝试一次。能进则进,不能进则退回来换条路再试试。
回溯的实现一般可以用 栈 也可以用 递归 。故DFS的实现一般用栈或者递归。
图的深度优先遍历示例
概述
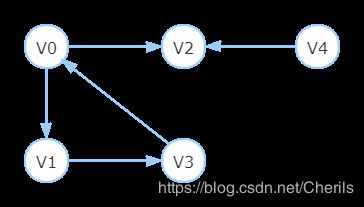
假设从V0开始遍历:
① V0有两个邻接点V1和V2(上述情况1),优先选择下标最小的(即第一个)邻接点V1开始遍历。
② 接着从V1开始遍历,V1只有一个邻接点V3(上述情况2),则不需要选择。
③ 接着遍历V3,V3只有一个邻接点V0,但是V0已经被遍历过(上述情况3),需要回溯。回溯V1,V1没有未被遍历过的邻接点;继续回溯V0,V0有一个未被遍历过的邻接点V2,则下一个遍历的顶点确定为V2。
④ 接着从V2开始遍历,V2无邻接点,且无法回溯(上述情况4),则需要检测visited[i],找到图里仍未被访问过的顶点只剩下V4了,则遍历V4,遍历结束。
遍历序列为:
V0-> V1-> V3-> V2-> V4
从其他顶点出发的深度优先遍历同理,遍历序列分别为:
V1-> V3-> V0-> V2-> V4
V2-> V0-> V1-> V3-> V4
V3-> V0-> V1-> V2-> V4
V4-> V2-> V0-> V1-> V3
图(邻接矩阵)的DFS实现(栈或递归)
图一般用邻接矩阵或邻接表这两种数据结构来实现存储。
递归实现:
- 访问顶点n,标记n已被访问,即visited[n]=1
- 求出i = 顶点n的下一个邻接点
- while(i 存在)
if(i未访问)
从顶点i出发递归执行该算法
i = 顶点v的下一个邻接点
/*
* 定义图的结构
* 用邻接矩阵存储图的边信息
*/
class Graph {
static final int MaxNum=20; //最大顶点数目
static final int MaxValue=65535;
char[] Vertex = new char[MaxNum]; //定义数组,保存顶点信息
int GType; //图的类型0:无向图 1:有向图
int VertxNum; //顶点的数量
int EdgeNum; //边的数量
int[][] EdgeWeight = new int[MaxNum][MaxNum]; //定义矩阵保存顶点信息
int[] isVisited = new int[MaxNum]; //遍历标志 1为已访问过,0为未访问过
//深度优先遍历 递归法
static void DeepTraOne(Graph g,int n){//从第n个顶点开始遍历
int i;
g.isVisited[n] = 1; //当前访问顶点n,将其visited[n]标记为1.
System.out.println("—>" + g.Vertex[n]); //输出顶点数据
//添加处理顶点的操作
for(i = 0; i< g.VertxNum; i++){
if(g.EdgeWeight[n][i] != g.MaxValue && g.isVisited[i] == 0){//若顶点n的第一个邻接点i存在,则顶点i出发执行该算法开始递归。
DeepTraOne(g, i); //递归进行遍历
}
}
}
栈(非递归)实现:
- 栈S初始化;将所有顶点都标记为未访问:visited[n] = 0;
- 访问顶点vertexIndex;将顶点v标记为已访问:visited[vertexIndex] = 1;顶点vertexIndex入栈S;
- while(栈S非空)
vertexIndex = 栈S的栈顶元素(不出栈)
if(存在并找到v的未被访问的邻接点nextVertexIndex )
访问nextVertexIndex ;visited[nextVertexIndex ] = 1;
nextVertexIndex 进栈;
else
vertexIndex 出栈;
/**
* 深度优先遍历
* @param vertexIndex 表示要遍历的起点,即图的邻接矩阵中的行数
*/
public void DFS(int vertexIndex) {
//定义一个栈
ArrayStack stack = new ArrayStack();
//1.添加检索元素vertexIndex到栈中 将该点标记为已访问
vertexList[vertexIndex].setVisited(true);
stack.push(vertexIndex);
//找到vertexIndex的邻接点nextVertexIndex
int nextVertexIndex = getNextVertexIndex(vertexIndex);
while(!stack.isEmpty()) {
//不断地压栈、出栈,直到栈为空(检索元素也没弹出了栈)为止
if(nextVertexIndex != -1) {
vertexList[nextVertexIndex].setVisited(true);
stack.push(nextVertexIndex);
stack.printElems();
} else {
stack.pop();
}
//检索当前栈顶元素是否包含其他未遍历过的节点
if(!stack.isEmpty()) {
nextVertexIndex = getNextVertexIndex(stack.peek());
}
}
}
树的深度优先遍历示例
常用的非线性数据结构有两种,分别是树和图。树是图的一种特殊情况。树的dfs和bfs可以直接用树的数据结构来实现,相比之下更简单且好理解一点。
树是图的一种,而图不一定是树。 树是有向无环图。
由于树是无环的,所以避免了图遍历会遇到的很多特殊情况,使得遍历的情形更加简单。一般树从根节点开始遍历。
概述
以二叉树为例
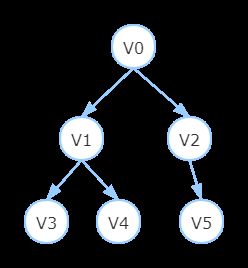
根据dfs遍历的策略,从V0出发的遍历序列为:
V0-> V1-> V3-> V4-> V2-> V5
树的DFS实现(栈或递归)
递归实现:
实际上是树的先序遍历。
树的先序遍历:首先访问根,再先序遍历左/右子树,最后先序遍历右/左子树。(根先 子树后)
树的中序遍历: 首先中序遍历左/右子树,再访问根,最后中序遍历右/左子树。(根在左右子树中间遍历)
树的后序遍历:首先后序遍历左(右)子树,再后序遍历右(左)子树,最后访问根。(子树先 根最后)
树的遍历都是递归。
//递归实现dfs
public void depthOrderTraversalWithRecursive()
{
depthTraversal(root);
}
private void depthTraversal(TreeNode tn)
{
if (tn!=null)
{
System.out.print(tn.value+" ");
depthTraversal(tn.left);
depthTraversal(tn.right);
}
}
栈(非递归)实现:
深度优先遍历运用到栈的“先进后出”的特性。
树的某节点的子节点即为这个节点的邻接点。
栈实现的主要操作:(主要有两种情况)
① 栈顶弹出(pop)哪个节点(即当前访问到哪个节点),则压入(push)哪个节点的子节点(从右往左push,这样出栈时候先pop的是左节点。所以下一步pop的就是当前节点的左节点即第一个邻接点)。
② 如果当前节点没有子节点,继续pop栈内剩余元素的栈顶,这其实就是回溯的过程。
pop出的节点顺序即为dfs的遍历序列。
如上二叉树遍历过程示例:
① 初始栈Stack为(),左为栈顶,右为栈底。
先push V0节点入栈,栈内目前为Stack(V0)
② pop V0,同时将V0的子节点V2,V1从右往左依次压入栈中,此时Stack(V1, V2),V1在栈顶。
③ pop V1,同时将V1的子节点V4,V3压入栈中,此时Stack(V3,V4,V2),V3在栈顶。
④ pop V3,V3没有子节点,出现上述情况二回溯,则继续pop,此时Stack(V4,V2),V4在栈顶。
⑤ pop V4,V4没有子节点,同上继续pop,此时Stack(V2),V2在栈顶
⑥ pop V2,V2有一个子节点V5,将V5压入栈中,此时Stack(V5),V5在栈顶
⑦ pop V5。所有节点遍历完,遍历结束。
最终栈pop顺序是V0-> V1-> V3-> V4-> V2-> V5
//栈实现dfs
public class Solution {
public ArrayList<Integer> PrintFromTopToBottom(TreeNode root) {
ArrayList<Integer> lists=new ArrayList<Integer>();
if(root==null)
return lists;
Stack<TreeNode> stack=new Stack<TreeNode>();
stack.push(root);
while(!stack.isEmpty()){
TreeNode tree=stack.pop();
//先往栈中压入右节点,再压左节点,这样出栈就是先左节点后右节点了。
if(tree.right!=null)
stack.push(tree.right);
if(tree.left!=null)
stack.push(tree.left);
lists.add(tree.val);
}
return lists;
}
}
BFS(Breadth-First-Search) 广度优先搜索/遍历
基本概念
从图中某个顶点v出发的广度优先搜索过程BFS可以描述为:
- 访问顶点v,并对v做已访问标记。
- 对于每个顶点v,依次访问v的各个未访问过的邻接点,接着再依次访问分别与这些邻接点相邻接且未访问过的顶点。
图中所有顶点,以及在遍历时经过的边(即从已访问的顶点到达未访问的顶点的边,个人理解就是遍历的路径)构成的子图,称为图的广度优先搜索生成树(或生成森林)。
BFS的遍历规则有两个重点:
- 先访问完当前顶点的所有邻接点
- 先访问顶点的邻接点 先于 后访问顶点的邻接点 被访问。
具体来说,给定一个图G =
在遍历时,如果出现图不连通的情况,和DFS中的解决方法一样,从头测试visited[i],找出剩余的未访问过的顶点,再按上述规则遍历。
图的广度优先遍历示例
概述

还是上图例子,假设从V0开始进行广度优先遍历:
① V0有两个邻接点V1和V2,依次遍历所有邻接点,故V0-> V1-> V2
② 因为V1先于V2被访问,所以先访问V1的所有邻接点即只有V3,此时V0-> V1-> V2-> V3
③ 接下来访问V2的所有邻接点,因V2无邻接点,只能看V3的邻接点。
④ V3的邻接点只有V0,而V0已被访问过。此时需检测visited[i],找到仅剩V4未被访问过,访问V4。遍历结束。
最终遍历序列为:V0-> V1-> V2-> V3-> V4
从其他顶点出发的遍历同理,序列分别为:
V1-> V3-> V0-> V2-> V4
V2-> V0-> V1-> V3-> V4
V3-> V0-> V1-> V2-> V4
V4-> V2-> V0-> V1-> V3
图的BFS实现(队列)
队列实现:
- 初始化队列Q; 将所有顶点标记为未访问:visited[n] = 0;
- 访问顶点i(一个for循环实现每个节点的广度优先遍历) : 第一步标记visited[i] = 1; 将顶点i插入队列Q;
- while(队列Q非空) //开始循环
队首元素i出队;
j = 节点i的邻接点(一个for循环,遍历出i的所有邻接点)
while( j 存在)
如果j未被访问,则访问j;
visited[j] = 1;
j 插入队列;
j++; //j = 节点i的下一个邻接点
static void BFS(Graph g){
Queue<Integer> queue = new LinkedList<Integer>(g.VertexNum);
int i,j;
for(i = 0; i < g.VertexNum; i++){ //初始化顶点的访问情况
g.isVisited[i] = 0;
}
for(i = 0; i < g.VertexNum; i++){ //遍历每一个顶点,实现从每一个顶点出发的广度优先遍历
g.isVisited[i] = 1;//将当前访问元素标记为已访问
System.out.println("->"+g.Vertex[i]);
queue.offer(i);//将节点i插入进队列
while(!queue.isEmpty()){ //队列空了才会跳出循环,意味着从某个顶点出发的广度优先遍历已经结束了,下次循环意味着要从另外一个顶点出发
vertex = queue.poll(); //将队首元素弹出 存入vertex[]数组中
for(j = 0; j < g.VertexNum; j++){
if(g.EdgeWeight[i][j] != g.MaxValue && g.isVisited[j] == 0){
//g.EdgeWeight[i][j] != g.MaxValue表示节点i的下一个邻接点j存在
System.out.println(g.Vertex[i]);
g.isVisited[j] = 1;
queue.offer(j);
}
}
}
}
}
树的广度优先遍历示例
概述
以二叉树为例

广度优先遍历,需要用到队列(Queue)来存储节点对象,队列的特点是“先进先出”。
队列实现的主要操作:
弹出队首的一个节点,则将该节点的所有子节点依次(下标从小到大)插入队列。如无子节点,则继续弹出队首元素重复上一步骤。
所以先往队列中插入左节点,再插右节点,这样出队就是先左节点后右节点了。队列依次弹出的节点顺序即为广度优先遍历序列。
示例:(上图二叉树的广度优先遍历过程)
① 初始化队列 Queue() 左为队首,右为队尾。右进左出。
首先将V0插入到队列中,此时队列内元素为Queue(V0);
② 将V0 弹出(此时得到V0节点),同时将V0的所有子节点V1、V2从左到右依次插入队列,此时Queue(V1,V2),V1在队首,V2在队尾。
③ 将队首元素V1 弹出,同时将V1的所有子节点V3、V4插入队列,此时Queue(V2,V3,V4),V2在队首,V4在队尾。
④ 将V2 弹出,同时将V2的所有子节点V5插入队列,此时Queue(V3,V4,V5),V3在队首,V5在队尾。
⑤ 将V3 弹出,V3无子节点可压入,则继续弹出,此时Queue(V4,V5)。
⑥ 将V4 弹出,V4无子节点可压入,继续弹出,此时Queue(V5)。
⑦ 将V5 弹出,V~5无子节点可压入。队列为空,遍历结束。
最终队列弹出顺序为V0-> V1-> V2-> V3-> V4-> V5
树的BFS实现(队列)
//队列bfs实现
public class Solution {
public ArrayList<Integer> PrintFromTopToBottom(TreeNode root) {
ArrayList<Integer> lists=new ArrayList<Integer>();
if(root==null)
return lists;
Queue<TreeNode> queue=new LinkedList<TreeNode>();
queue.offer(root);
while(!queue.isEmpty()){
TreeNode tree=queue.poll();
if(tree.left!=null)
queue.offer(tree.left);
if(tree.right!=null)
queue.offer(tree.right);
lists.add(tree.val);
}
return lists;
}
}
参考:
[1] 图的遍历:深度优先遍历和广度优先遍历
[2] 数据结构:图的遍历–深度优先、广度优先
[3] 树的广度优先遍历和深度优先遍历(递归非递归、Java实现)
[4] 《图论》——图的存储与遍历(Java)
[5] 图论——深度优先遍历和广度优先遍历(Java)
[6] Java编程实现基于图的深度优先搜索和广度优先搜索完整代码