pandas绘图 (plot(),hist(),scatter()、折线图、柱状图、直方图、散布图)

1 numpy.cumsum()

numpy.cumsum(a, axis=None, dtype=None, out=None)

axis=0，按照行累加。
axis=1，按照列累加。
axis不给定具体值，就把numpy数组当成一个一维数组。

现在看一看例子

a = np.arange(6).reshape((2, 3))
a = [[0, 1, 2],
     [3, 4, 5]]

要是直接

numpy.cumsum(a)

得到 [ 0 1 3 6 10 15] -----------------这是一个一维数组，不断累加

numpy.cumsum(a, axis=0)

得到
[[0 1 2]
[3 5 7]]
这是以[0 1 2]这个为基准，累加。output的形状和a的相同

numpy.cumsum(a, axis=1)

得到
[[ 0 1 3]
[ 3 7 12]]
这是以[0 3]这个为基准，累加。output的形状同样与a的相同

因为a是二维数组，所以axis只有0，1
当a是更高维度的时候，axis会更加多

原文链接：https://blog.csdn.net/Hsu8506/article/details/83715291

cumsum() 累加值，新生成的数+上一个生成的数

cumsum(0) 看几行几列式，按行叠加，行内的叠加值相同

cumsum(1) 按行叠加，新生成的数+上一个生成的数

2 知识点

散布图  是观察两个一维数据序列之间关系的有效手段
log() 对数
diff() 沿着指定轴计算第N维的离散差值   #diff函数返回一个由相邻数组元素的差值构成的数组
dropna()  dropna()函数返回一个包含非空数据和索引值的Series

crosstab()
ix()

random.rand(num):生成的随机数是0-1中的

3 pandas绘制图形，填充数据，matplotlib展示数据

#pandas绘制图形，填充数据（创建figure，填充数据），matplotlib展示数据
s=pd.Series(np.random.randn(10).cumsum(),index=np.arange(0,100,10))
s.plot()
plt.show()

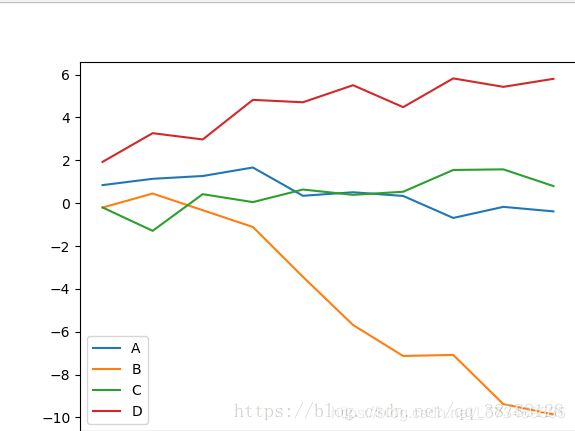
df=pd.DataFrame(np.random.randn(10,4).cumsum(0),columns=['A','B','C','D'],index=np.arange(0,100,10))
 
print(df)
df.plot()
plt.show()

4 柱状图

'''
柱状图
random.rand(num):生成的随机数是0-1中的
'''
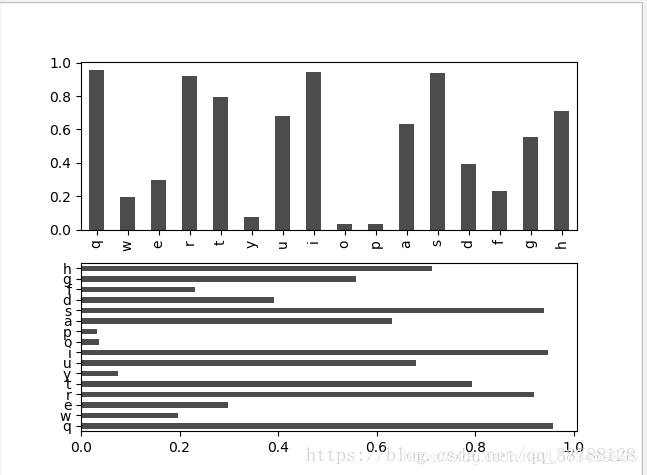
fig,axes=plt.subplots(2,1)
data=pd.Series(np.random.rand(16),index=list('qwertyuiopasdfgh'))
#竖向展示
data.plot(kind='bar',ax=axes[0],color='k',alpha=0.7)
 
#横向展示  stacked=True叠加值
data.plot(kind='barh',ax=axes[1],stacked=True,color='k',alpha=0.7)
 
 
plt.show()'''
柱状图
random.rand(num):生成的随机数是0-1中的
'''
fig,axes=plt.subplots(2,1)
data=pd.Series(np.random.rand(16),index=list('qwertyuiopasdfgh'))
#竖向展示
data.plot(kind='bar',ax=axes[0],color='k',alpha=0.7)
 
#横向展示  stacked=True叠加值
data.plot(kind='barh',ax=axes[1],stacked=True,color='k',alpha=0.7)
 
 
plt.show()

5 堆积柱状图

'''
有关小费的数据集
crosstab()
ix()
'''
tips=pd.read_csv('C:\\tools\\pydata-book-master\\ch08\\tips.csv')
print(tips)
#下面是一个例子：做一张堆积柱状图来显示每天各种聚会规模的数据点百分比
party_counts = pd.crosstab(tips.day,tips['size'])
print (party_counts)
# size  1   2   3   4  5  6
# day
# Fri   1  16   1   1  0  0
# Sat   2  53  18  13  1  0
# Sun   0  39  15  18  3  1
# Thur  1  48   4   5  1  3
 
 
#ix的下标从0开始bug
party_counts = party_counts.ix[0:,2:5]
print (party_counts)
# size   2   3   4  5
# day
# Fri   16   1   1  0
# Sat   53  18  13  1
# Sun   39  15  18  3
# Thur  48   4   5  1
#然后进行归一化是各行和为1
party_pcts = party_counts.div(party_counts.sum(1).astype(float),axis = 0)
print (party_pcts)
party_pcts.plot(kind = 'bar',stacked = True)
plt.show()#证明周末的聚会规模大

6 直方图

'''
每天各种聚会的比例的直方图
'''
tips['pct']=tips['tip']/tips['total_bill']
tips['pct'].hist(bins=50)
plt.show()
 
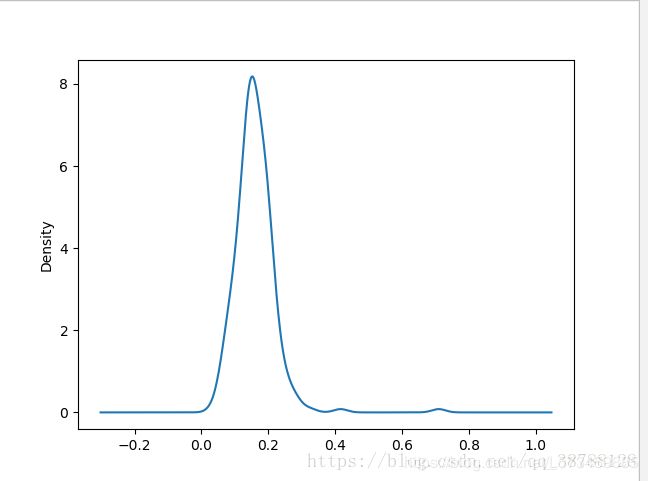
#与此相关的是密度图：他是通过计算“可能会产生观测数据的连续概率分布的估计”
#而产生的。一般的过程将该分布金思维一组核（诸如正态之类的较为简单的分布）。
#此时的密度图称为KDE图。kind = ‘kde’即可。
#消费百分比密度图
tips['pct'].plot(kind = 'kde')
plt.show()

7 双峰分布

#两个不同的正态分布组成的双峰分布
comp1 = np.random.normal(0,1,size = 200)
comp2 = np.random.normal(10,2,size = 200)
values = pd.Series(np.concatenate([comp1,comp2]))
print (values)
values.hist(bins = 100,alpha = 0.3,color = 'k',normed = True)
values.plot(kind = 'kde',style = 'k--')
plt.show()

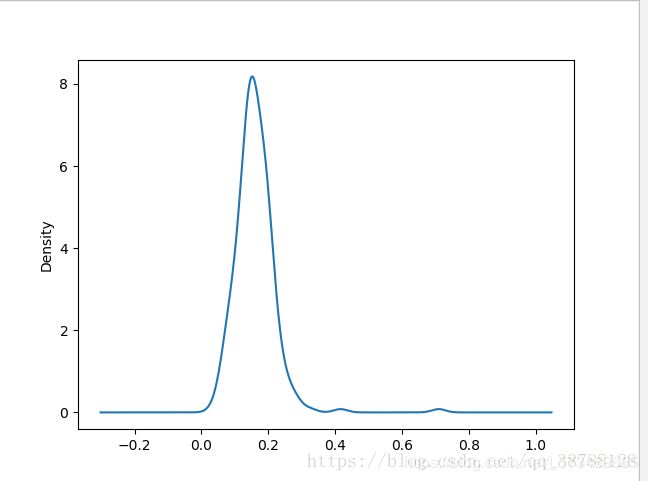
8 百分比密度图

#消费百分比密度图
tips['pct'].plot(kind = 'kde')
plt.show()

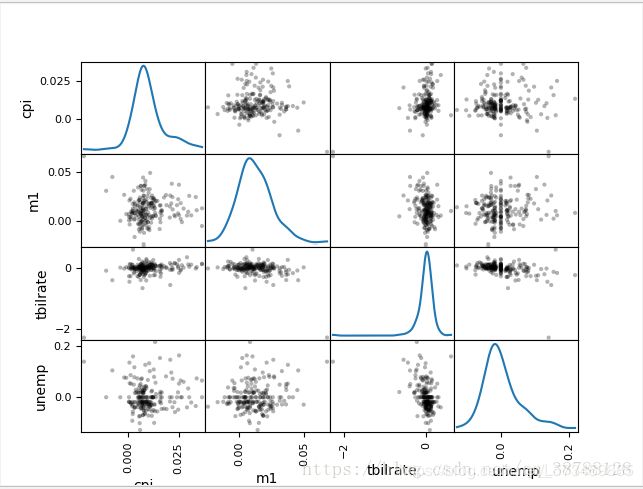
9 散布图

'''
散布图  是观察两个一维数据序列之间关系的有效手段
log() 对数
diff() 沿着指定轴计算第N维的离散差值   #diff函数返回一个由相邻数组元素的差值构成的数组
dropna()  dropna()函数返回一个包含非空数据和索引值的Series
'''
data=pd.read_csv('C:\\tools\\pydata-book-master\\ch08\\macrodata.csv')
print(data)
data=data[['cpi','m1','tbilrate','unemp']]
#计算对数差
trans_data=np.log(data).diff().dropna()
print(trans_data)
 
 
#利用对数差绘制两列之间的散布图
plt.scatter(trans_data['m1'],trans_data['unemp'])
plt.title('%s vs %s'%('m1','unemp'))
plt.show()

#散布图矩阵 观察不同列之间的散布图；
# 对角线放置各变量的直方图和密度图
pd.scatter_matrix(trans_data,diagonal='kde',color='k',alpha=0.3)

原文链接：https://blog.csdn.net/qq_38788128/article/details/80813968