Fisher的判别推导

一、Fisher算法的主要思想
线性判别分析(Linear Discriminant Analysis，简称LDA)是一种经典的线性学习方法，在二分类问题上因为最早由【Fisher，1936年】提出，所以也称为“Fisher 判别分析！”
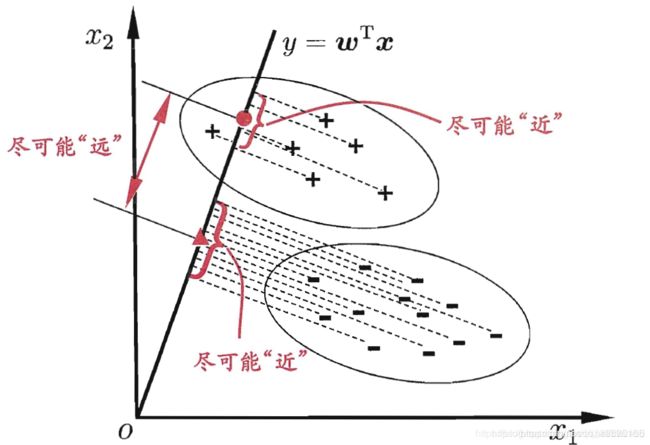
Fisher（费歇）判别思想是投影，使多维问题简化为一维问题来处理。选择一个适当的投影轴,使所有的样本点都投影到这个轴上得到一个投影值。对这个投影轴的方向的要求是：使每一类内的投影值所形成的类内离差尽可能小，而不同类间的投影值所形成的类间离差尽可能大。

二、Fisher数学算法步骤
为了找到最佳投影方向，需要计算出 各类样本均值、样本类内离散度矩阵 Si\boldsymbol S_{i}S i和样本总类内离散度矩阵 Sw\boldsymbolS_{w}Sw、样本类间离散度矩阵 Sb\boldsymbol S_{b}Sb ，根据Fisher准则，找到最佳投影向量，将训练集内的所有样本进行投影，投影到一维Y空间，由于Y空间是一维的，则需要求出Y空间的划分边界点，找到边界点后，就可以对待测样本进行一维Y空间投影，判断它的投影点与分界点的关系，将其归类。具体方法如下(以两类问题为例子)：
①计算各类样本均值向量MI，Mi是各个类的均值，Ni是Wi 类的样本个数。

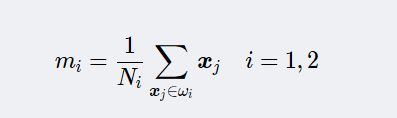
②计算样本类内离散度矩阵Si和总类内离散度矩阵Sw。

③计算样本类间离散度矩阵Sb。

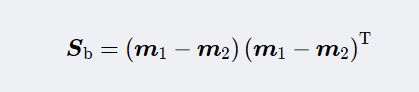
④求投影方向向量 WWW (维度和样本的维度相同)。我们希望投影后，在一维YYY空间里各类样本尽可能分开，就是我们希望的两类样本均值之差(m1¯¯¯¯¯−m2¯¯¯¯¯)越大越好，同时希望各类样本内部尽量密集，即是：希望类内离散度越小越好。因此，我们可以定义Fisher准则函数为：

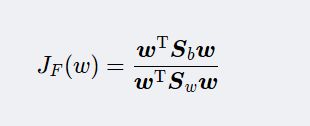
⑤将训练集内所有样本进行投影。

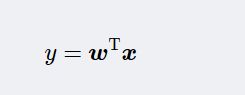
⑥. 计算在投影空间上的分割阈值y0，在一维Y空间，各类样本均值mi¯为:

样本类内离散度Si¯2和总类内离散度 Sw¯

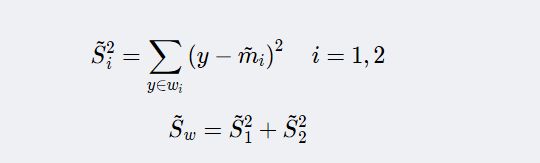
而此时类间离散度就成为两类均值差的平方。

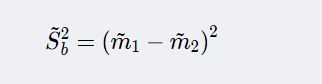
计算阈值y0
​

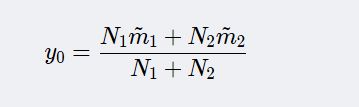
⑦对于给定的测试样本x，计算出它在w上的投影点y

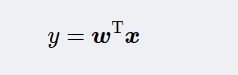
⑧根据决策规则分类！

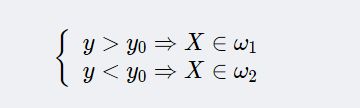
三、python代码实现
1.数据生成

from sklearn.datasets import make_multilabel_classification
import numpy as np

x, y = make_multilabel_classification(n_samples=20, n_features=2,
                                      n_labels=1, n_classes=1,
                                      random_state=2)  # 设置随机数种子，保证每次产生相同的数据。

# 根据类别分个类
index1 = np.array([index for (index, value) in enumerate(y) if value == 0])  # 获取类别1的indexs
index2 = np.array([index for (index, value) in enumerate(y) if value == 1])  # 获取类别2的indexs

c_1 = x[index1]   # 类别1的所有数据(x1, x2) in X_1
c_2 = x[index2]   # 类别2的所有数据(x1, x2) in X_2

2、fisher算法实现

def cal_cov_and_avg(samples):
    """
    给定一个类别的数据，计算协方差矩阵和平均向量
    :param samples:
    :return:
    """
    u1 = np.mean(samples, axis=0)
    cov_m = np.zeros((samples.shape[1], samples.shape[1]))
    for s in samples:
        t = s - u1
        cov_m += t*t.reshape(2, 1)
    return cov_m, u1
def fisher(c_1, c_2):
    """
    fisher算法实现(参考上面的推导公式进行理解)
    :param c_1:
    :param c_2:
    :return:
    """
    cov_1, u1 = cal_cov_and_avg(c_1)
    cov_2, u2 = cal_cov_and_avg(c_2)
    s_w = cov_1 + cov_2          # 总类内离散度矩阵。
    u, s, v = np.linalg.svd(s_w) # 下面的参考公式（4-10）
    s_w_inv = np.dot(np.dot(v.T, np.linalg.inv(np.diag(s))), u.T)
    return np.dot(s_w_inv, u1 - u2)

3、判断类别

def judge(sample, w, c_1, c_2):
    """
    返回值：ture 属于1；false 属于2
    :param sample:
    :param w:
    :param c_1:
    :param c_2:
    :return:
    """
    u1 = np.mean(c_1, axis=0)
    u2 = np.mean(c_2, axis=0)
    center_1 = np.dot(w.T, u1) # 参考公式(2-8)
    center_2 = np.dot(w.T, u2)
    pos = np.dot(w.T, sample)  # 新样本进来判断
    return abs(pos - center_1) < abs(pos - center_2)

w = fisher(c_1, c_2)             # 调用函数，得到参数w
out = judge(c_2[1], w, c_1, c_2) # 判断所属的类别。
print(out)

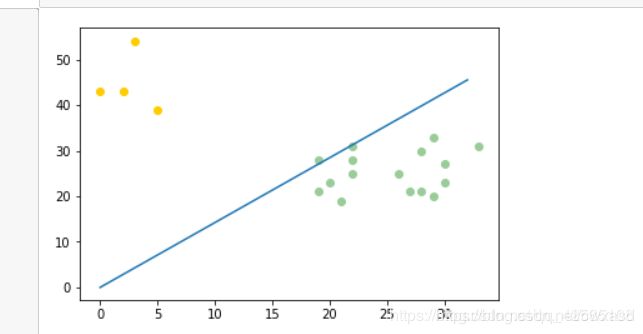
4.绘图

plt.scatter(c_1[:, 0], c_1[:, 1], c='red')
plt.scatter(c_2[:, 0], c_2[:, 1], c='blue')
line_x = np.arange(min(np.min(c_1[:, 0]), np.min(c_2[:, 0])),
                   max(np.max(c_1[:, 0]), np.max(c_2[:, 0])),
                   step=1)
line_y = -(w[0]*line_x) / w[1]
plt.plot(line_x, line_y, linewidth=3.0,  label = 'fisher boundary line ')
plt.legend(loc='upper right')
plt.xlabel('feature 1')
plt.ylabel('feature 2')
plt.show()

5.运行结果：