153. Find Minimum in Rotated Sorted Array

1题目理解

输入：一个按升序排序的数组nums，但是这个数组在某个位置被旋转了。(例如., 原始数组是[0,1,2,4,5,6,7]，旋转后就变成 [4,5,6,7,0,1,2])。
输出：这个数组的最小值
要求：O(lgn)时间复杂度

示例1
Input: [3,4,5,1,2]
Output: 1

示例2
Input: [4,5,6,7,0,1,2]
Output: 0

2 二分+分治法

使用分治法，同时利用在每一个中点，nums左右两部分，至少有一部分是有序的，可以在有序数组内使用O(1)的时间找到最小值nums[l]。
下面的内容来自 花花酱解题原文链接。

2.1至少有一部分是有序的

一个有序数组一定有nums[0]

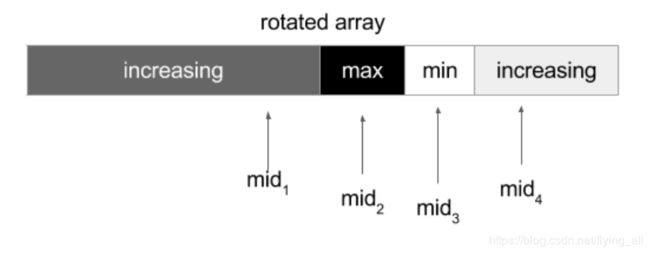
在被旋转的数组内，我们遇到的mid可能在上升子数组内、可能恰好是最大值，可能恰好是最小值，也可能在后续的一个上升子数组内。

mid位置	左边有序	右边有序
mid1	true	false
mid2	true	false
mid3	true	true
mid4	false	true

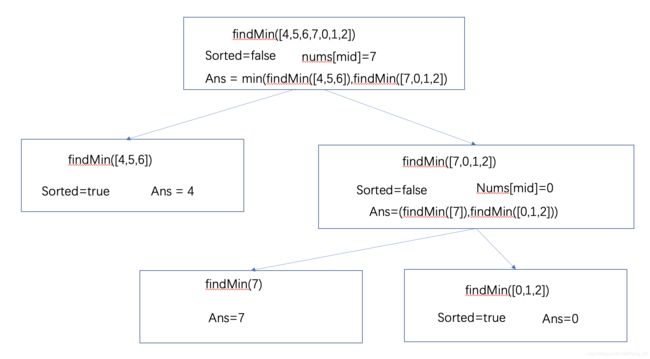
2.2 示例

2.3 编码

class Solution {
    public int findMin(int[] nums) {
        return findMin(nums,0,nums.length-1);
    }
    
    private int findMin(int[]  nums,int l ,int r){
        if(l+1>=r) return Math.min(nums[l],nums[r]);
        if(nums[l]<nums[r]) return nums[l];
        int mid = l + ((r-l)>>1);
        return Math.min(findMin(nums,l,mid-1>=0?mid-1:l), findMin(nums,mid,r));
        
    }
}

3 只有二分

来源网页地址
该方法不太好理解。

我们分析一下在不同情况下，最小元素位于左子数组还是右边子数组

mid位置	与起始元素比较大小	最小元素在哪里
mid1	nums[mid]>nums[l]	右边子数组
mid2	nums[mid]>nums[l]	右边子数组
mid3	nums[mid]	就是元素本身
mid4	nums[mid]	左边子数组

当处于mid3的时候，我们发现nums[mid-1]>nums[mid] ，这启发我们需要找到停止搜索的条件。
在正常升序的数组中，一定有nums[mid] 我们会发现如果nums[mid-1]>nums[mid]，那么nums[mid]是最小值。如果nums[mid]>nums[mid+1]，那么nums[mid+1]是最小值。

class Solution {
    public int findMin(int[] nums) {
        int l = 0 ,r = nums.length-1;
        if(nums[r]>nums[l]) return nums[l];
        while(l<=r){
            if(l==r) return nums[l];
            int mid = l+((r-l)>>1);
            if(nums[mid]>nums[mid+1]){
                return nums[mid+1];
            }
            if(nums[mid-1]>nums[mid]){
                return nums[mid];
            }
            
            if(nums[l]<nums[mid]){
                l = mid+1;
            }else{
                r = mid -1;
            }
        }
        return -1;
    }  
}