常用排序算法(冒泡排序,快速排序,堆排序)
这是常用的一些基本排序算法.
数据结构
先定义公共的数据结构
typedef int KeyType;
typedef struct {
KeyType key;
}RecType;
typedef RecType SeqSortList[MAXSIZE+1];//表中的0元素空着或用作哨兵单元
一般把数组中的第0个位置预留出来,就是为了作为哨兵,进行两个数据进行交换时,可以把哨兵作为临时变量进行交换.
公共方法:
//打印集合
void logSort(SeqSortList R,int start,int end);
打印数组集合: R:数组对象. start:开始打印的角标. end:结束打印的角标.
void logSort(SeqSortList R,int start,int end){
printf("[");
for(int i=start;i<=end;i++){
if(i==start){
printf("%d",R[i].key);
}else{
printf(",%d",R[i].key);
}
}
printf("]");
}
堆排序
1.排序思想
第一步创建大根堆(或者小根堆)
第二步步骤:取堆顶关键字与无序区最后一个元素互换.然后剩下的无序区元素进行第一步.
最后直到无序区元素为1个,结束循环.
注意:大根堆或者小根堆是完全二叉树.
2.完全二叉树
待排序数组R=[10,15,56,6,33,5,26,8]
完全二叉树:

3.创建大根堆
这里以建立大根堆为例:
若 结点位置为: i ,其左孩子位置: 2*i, 其右孩子位置: 2*i+1.
先判断左孩子和右孩子的最大值, 如果 i 结点的值小于其左孩子和右孩子的最大值,则 i 结点与最大值位置的互换.否则不用调整.
最后就是 i 结点的值大于其左孩子(2*i)的值和右孩子(2*i+1)的值.
注意:堆排序中大根堆(小根堆)是完全二叉树为基础.
一共有8个结点,

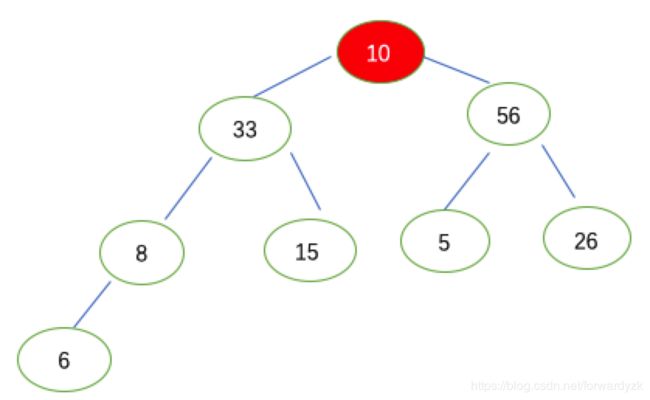
建大根堆第一步: 从第4个结点(6)判断是否需要调整:
第4个结点小于其左孩子,需要调整,6和8互换.结果为下图.
建大根堆第二步:第3个结点(56)判断是否需要调整:
第3个结点大于其左孩子和右孩子,不需要调整.结果为下图:

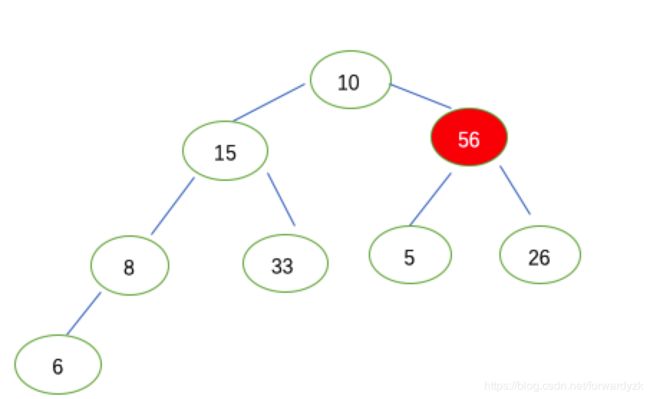
建大根堆第三步: 第2个结点(15)判断是否需要调整:
第2个结点小于其右孩子,则15月33互换位置.结果为下图:
建大根堆第四步: 第1个结点(10)判断是否需要调整:
第1个结点小于其左孩子和右孩子,右孩子大于左孩子,所以10与56互换位置.
互换后:10又小于其右孩子26,所以10月26位置还要互换一次.结果为下图:

到此大根堆已经建立完成:
4.堆排序
大根堆创建完成后,其实还是无序的.
下面一步就是取关键字的步骤.
1.每次都取堆顶,然后与无序区的最后一个记录进行交换,
2.然后再将剩下的区域再走一次创建大根堆.
然后重复1和2步骤,直到无序区的结点个数为1
下面进行取关键字的步骤:

取关键字第一步:取堆顶元素56,与无序区最后一个元素6互换位置(56加入了有序区),然后再把剩下的无序区走一遍建立大根堆,结果为下面的图.
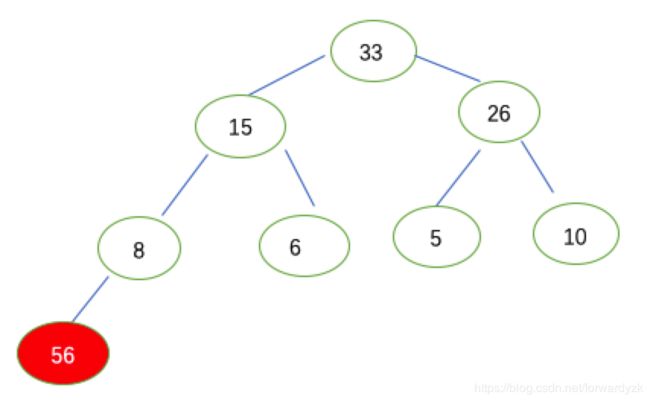
取关键字第二步:取堆顶元素33,与无序区最后一个元素10互换位置(33加入了有序区),然后再把剩下的无序区走一遍建立大根堆,结果为下面的图.

取关键字第三步:取堆顶元素26,与无序区最后一个元素5互换位置(26加入了有序区),然后再把剩下的无序区走一遍建立大根堆,结果为下面的图.

取关键字第四步:取堆顶元素15,与无序区最后一个元素6互换位置(15加入了有序区),然后再把剩下的无序区走一遍建立大根堆,结果为下面的图.
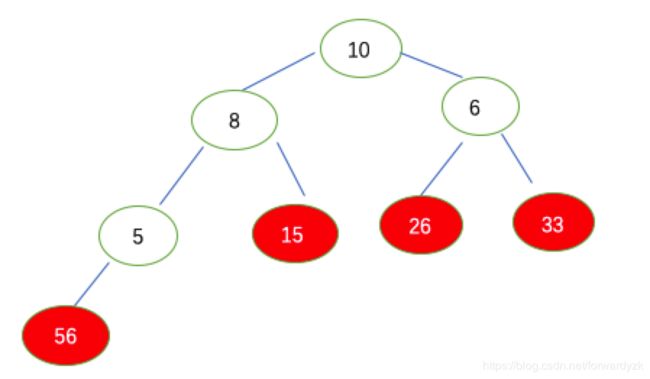
取关键字第五步:取堆顶元素10,与无序区最后一个元素5互换位置(10加入了有序区),然后再把剩下的无序区走一遍建立大根堆,结果为下面的图.
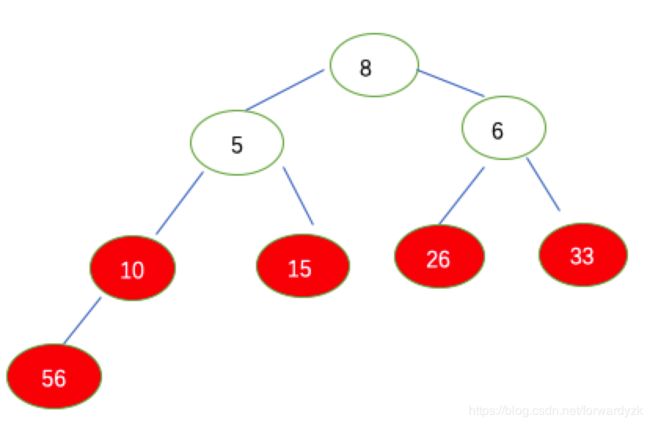
取关键字第六步:取堆顶元素8,与无序区最后一个元素6互换位置(8加入了有序区),然后再把剩下的无序区走一遍建立大根堆,结果为下面的图.

取关键字第七步:取堆顶元素6,与无序区最后一个元素5互换位置(6加入了有序区),然后再把剩下的无序区走一遍建立大根堆,结果为下面的图.

此时无序区就剩下了一个结点,取关键字结束.
最后的有序的完全二叉树为:
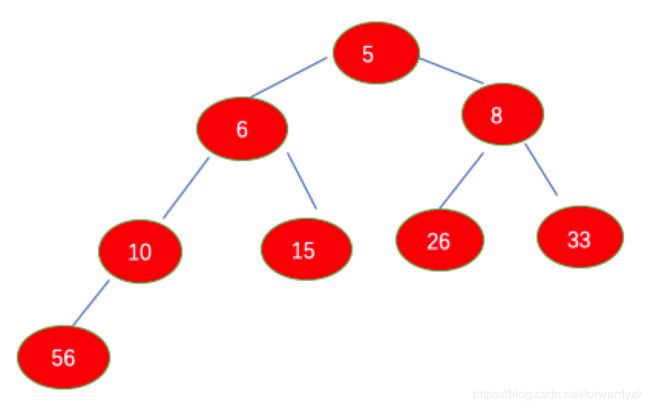
有序的数组为顺序读取二叉树[5,6,8,10,15,26,33,56].
5.算法运行结果
6.算法实现
//一次堆排序.
void Sift(SeqSortList R,int i,int h){
//将R[i...h]调整为大堆跟,假定R[i]的左右孩子均满足堆的性质
int j;
RecType x=R[i];
j=2*i;
while (j<=h) {//当R[i]的左孩子不为空时执行循环
if(j<h && R[j].key<R[j+1].key)
j++;//若右孩子的关键字较大,j++.置为右孩子角标
if(x.key>R[j].key)//表示当前x大于其左右孩子,找到了x的位置
break;
R[i]=R[j];//将大于i位置的置为双亲的位置
i=j;j=2*i;//然后修改i和j,重新调整指向,重新查找位置.
}
R[i]=x;
}
//堆排序
void HeapSort(SeqSortList R,int n){
//对R[1..h]进行堆排序,设置R[0]为暂存单元
int i;
//这里的循环是建立大堆
for(i=n/2;i>=1;i--)
Sift(R, i, n);
printf("大根堆:");
logSort(R, 1, n);
printf("\n");
for(i=n;i>1;i--){//对R[1..h]进行n-1此堆排序,取出了n-1个数据,剩下的一个数据,自然就是最小的.
R[0]=R[1];R[1]=R[i];R[i]=R[0];//每次都R[1]为最大的,将R[1]与R[i]进行互换,
Sift(R, 1, i-1);//然后再让//下面是对R[1...i-1]建立堆排序
printf("取关键字%d后的完全二叉树:",R[0]);
logSort(R, 1, n);
printf("\n");
}
}
int n=8;
SeqSortList R;
R[0].key=0;//哨兵
R[1].key=10;
R[2].key=15;
R[3].key=56;
R[4].key=6;
R[5].key=33;
R[6].key=5;
R[7].key=26;
R[8].key=8;
printf("无序R=");
logSort(R, 1, n);
printf("\n");
HeapSort(R, n);
printf("有序R=");
logSort(R, 1, n);
printf("\n");
双向冒泡排序
1.排序思想
例如:有n个数据.
1.遍历[n--------->1]位置.从底部(n位置)往上查找最小的值,放到第1位置.
2.遍历[2--------->n]位置,从第2个位置往底部查找最大值,放到第n位置.
3.遍历[n-1------>2]位置,从第n-1位置往上查找最小值,放在第2位置.
4.遍历[3-------->n-1]位置,从第2个位置往底部查找最大值,放到第n-1位置.
最多遍历n-1次,就可以排序好, 不管查找最大值和最小值的时,判断的时候也许就和邻数据做了交换,所以有时候遍历不到n-1次,剩下的就已经排序好了(除非原来的待排序的数组是逆序的),就没必要再继续判断,这个是通过一个标记变量来判断的.
每一次循环前置为flag=0.如果做了数据交换,则置为flag=1. 每次循环前,如果flag=0,则继续循环,如果flag==1,则结束循环,表明此时数组已经是有序的了.
2.算法例子和运行结果

i=1.表示进行的两次循环,从1-n 和n-1 两次遍历, 分别查找最小值和最大值.
然后分别放在了两边有序的位置.
从例子上可以看出,这是循环了2*2次,中间待循环的数组已经是有序的了.
3.算法的实现
//双向冒泡排序
void DboubbleSort(SeqSortList R,int n){
//从下往上查找小的,从上往下找大的
int i=1,j;
int NoSwap;
NoSwap=1;//表示是否有交换,默认的为有交换,无序
printf("[有序][无序][有序]\n");
while(NoSwap){
NoSwap=0;//先设置为无交换
//从下往上找最小的
for(j=n-i+1;j>=i+1;j--)
if(R[j].key<R[j-1].key){
R[0]=R[j];
R[j]=R[j-1];
R[j-1]=R[0];
NoSwap=1;
}
//此时第i个位置存储的是小的,
//那么从第i+1个位置开始往下找,最大的.
//从上往下找最大的
for(j=i+1;j<=n-i;j++)
if(R[j].key>R[j+1].key){
R[0]=R[j];
R[j]=R[j+1];
R[j+1]=R[0];
NoSwap=1;
}
printf("i=%d\n",i);
logSort(R, 1, i);
logSort(R, i+1, n-i);
logSort(R, n-i+1, n);
printf("\n");
i=i+1;
}
}
快速排序
1.排序思想
1.每次取待排序数组的第一个的数据(x),然后将当前的待排序的数组进行划分.划分成三部分. (小于x的数组)(x)(大于x的数组).
2.然后再对 (小于x的数组)和 (小于x的数组)进行划分.就这样递归调用.
2.算法例子和运行结果
3.算法的实现
//快速排序中的--划分方法
int Partition(SeqSortList R,int i,int j){
//=========
printf("划分前:");
int low=i;//只为打印用
int height=j;////只为打印用
logSort(R, low, height);
printf("\n");
//========
//对R[i]~R[j]区间内的记录进行一次划分排序
RecType x=R[i];//用区间第一个记录为基准
while(i<j){
//先从后面往前找第一个小于基准的值,赋给R[i]
while (i<j && R[j].key>=x.key) {
j--;
}
//找到了小于基准的值,赋给R[i]
if(i<j){
R[i]=R[j];
//这里i++,下面从从前面往后找第一个大于x的时候,从后一个开始查找
i++;
}
//然后从R[i]位置开始向后找,第一个大于x的值,赋给R[j].
while(i<j&& R[i].key<=x.key){
i++;
}
if(i<j){
R[j]=R[i];
j--;
}
}
R[i]=x;
//=========
printf("划分后:");
logSort(R, low, i-1);
logSort(R, i, i);
logSort(R, i+1, height);
printf("\n");
//========
return i;
}
//快速排序方法
void QuickSort(SeqSortList R,int low,int hight){
int p;
if(low<hight){
p=Partition(R, low, hight);
QuickSort(R, low, p-1);
QuickSort(R, p+1, hight);
}
}
冒泡排序
直接选择排序
直接插入排序
请查看这篇文章:
https://blog.csdn.net/forwardyzk/article/details/53640901
箱排序
基数排序
请查看这篇文章:
https://blog.csdn.net/forwardyzk/article/details/102935430