高等数学复习笔记(二)- 一元函数微分学的概念、计算以及几何应用
本节为高等数学复习笔记的第二部分,一元函数微分学的概念,计算以及几何应用,主要包括: 导数的定义,高阶导数的求解,极值点判断的充分条件,凹凸性判断的充分条件,拐点判断的充分条件与必要条件,渐近线以及复杂函数图形的作图方法。
1. 导数定义
f ′ ( x 0 ) = d f d x ∣ x = x 0 = l i m Δ x → 0 x 0 + Δ x Δ x = l i m x → x 0 f ( x ) − f ( x 0 ) x − x 0 f'(x_0)=\frac{df}{dx}|_{x=x_0}=lim_{\Delta x \rightarrow0}\frac{x_0+\Delta x}{\Delta x}=lim_{x\rightarrow x_0}\frac{f(x)-f(x_0)}{x-x_0} f′(x0)=dxdf∣x=x0=limΔx→0Δxx0+Δx=limx→x0x−x0f(x)−f(x0),下面看一道例题:
e g . 设 δ < 0 , f ( x ) 在 [ − δ , δ ] 上 有 定 义 , f ( 0 ) = 1 , 且 有 l i m x → 0 l n ( 1 − 2 x ) + 2 x f ( x ) x 2 = 0 , 证 明 : f ( x ) 在 x = 0 处 可 导 并 求 f ′ ( x ) 。 eg.设\delta<0,f(x)在[-\delta,\delta]上有定义,f(0)=1,且有lim_{x\rightarrow 0}\frac{ln(1-2x)+2xf(x)}{x^2}=0,证明:f(x)在x=0处可导并求f'(x)。 eg.设δ<0,f(x)在[−δ,δ]上有定义,f(0)=1,且有limx→0x2ln(1−2x)+2xf(x)=0,证明:f(x)在x=0处可导并求f′(x)。
解 : l i m x → 0 l n ( 1 − 2 x ) + 2 x f ( x ) x 2 = l i m x → 0 − 2 x − 1 2 ( − 2 x ) 2 + o ( x 2 ) + 2 x f ( x ) x 2 ( 泰 勒 展 开 ) = 2 l i m x → 0 f ( x ) − 1 x − 2 + 0 = 0 , 即 l i m x → 0 f ( x ) − 1 x = l i m x → 0 f ( x ) − f ( 0 ) x − 0 = 1 , 即 f ( x ) 在 x = 0 处 可 导 且 f ′ ( x ) = 1 。 解:lim_{x\rightarrow 0}\frac{ln(1-2x)+2xf(x)}{x^2}=lim_{x\rightarrow 0}\frac{-2x-\frac12(-2x)^2+o(x^2)+2xf(x)}{x^2}(泰勒展开)=2lim_{x\rightarrow 0}\frac{f(x)-1}{x}-2+0=0,即lim_{x\rightarrow 0}\frac{f(x)-1}{x}=lim_{x\rightarrow 0}\frac{f(x)-f(0)}{x-0}=1,即f(x)在x=0处可导且f'(x)=1。 解:limx→0x2ln(1−2x)+2xf(x)=limx→0x2−2x−21(−2x)2+o(x2)+2xf(x)(泰勒展开)=2limx→0xf(x)−1−2+0=0,即limx→0xf(x)−1=limx→0x−0f(x)−f(0)=1,即f(x)在x=0处可导且f′(x)=1。
2. 高阶导数
泰 勒 展 开 ( x = 0 处 ) : y = f ( x ) = Σ n = 0 ∞ f ( n ) ( 0 ) n ! x n 泰勒展开(x=0处):y=f(x)=\Sigma_{n=0}^{\infty}\frac{f^{(n)}(0)}{n!}x^n 泰勒展开(x=0处):y=f(x)=Σn=0∞n!f(n)(0)xn,看一道例题:
e g . y = f ( x ) = x 3 s i n x , 求 y ( 6 ) ( 0 ) 。 eg.y=f(x)=x^3sinx,求y^{(6)}(0)。 eg.y=f(x)=x3sinx,求y(6)(0)。
解 : 1 ) 展 开 : 由 于 y = x 3 s i n x 无 穷 阶 可 导 , 可 先 抽 象 展 开 为 y = Σ n = 0 ∞ f ( n ) ( 0 ) n ! x n ; 2 ) 又 由 于 y = x 3 s i n x = x 3 ( x − 1 6 x 3 + o ( x 3 ) ) = x 4 − 1 6 x 6 + o ( x 6 ) ; 3 ) 根 据 展 开 式 的 唯 一 性 , 比 较 1 ) 2 ) 两 步 , y ( 6 ) ( 0 ) 6 ! = − 1 6 , 可 得 y ( 6 ) ( 0 ) = − 1 20 。 解:1) 展开:由于y=x^3sinx无穷阶可导,可先抽象展开为y=\Sigma_{n=0}^{\infty}\frac{f^{(n)}(0)}{n!}x^n;2) 又由于y=x^3sinx=x^3(x-\frac16x^3+o(x^3))=x^4-\frac16x^6+o(x^6);3) 根据展开式的唯一性,比较1)2)两步,\frac{y^{(6)}(0)}{6!}=-\frac16,可得y^{(6)}(0)=-\frac1{20}。 解:1)展开:由于y=x3sinx无穷阶可导,可先抽象展开为y=Σn=0∞n!f(n)(0)xn;2)又由于y=x3sinx=x3(x−61x3+o(x3))=x4−61x6+o(x6);3)根据展开式的唯一性,比较1)2)两步,6!y(6)(0)=−61,可得y(6)(0)=−201。
几个常见的展开式(x=0处):
- e x = Σ n = 0 ∞ x n n ! = 1 + x + x 2 2 + . . . + x n n e^x=\Sigma_{n=0}^{\infty}\frac{x^n}{n!}=1+x+\frac{x^2}{2}+...+\frac{x^n}{n} ex=Σn=0∞n!xn=1+x+2x2+...+nxn
- 1 1 + x = Σ n = 0 ∞ ( − 1 ) n x n = 1 − x + x 2 − + . . . + ( − 1 ) n x n \frac{1}{1+x}=\Sigma_{n=0}^{\infty}(-1)^nx^n=1-x+x^2-+...+(-1)^nx^n 1+x1=Σn=0∞(−1)nxn=1−x+x2−+...+(−1)nxn
- 1 1 − x = Σ n = 0 ∞ x n = 1 + x + x 2 + . . . + x n \frac{1}{1-x}=\Sigma_{n=0}^{\infty}x^n=1+x+x^2+...+x^n 1−x1=Σn=0∞xn=1+x+x2+...+xn
- l n ( 1 + x ) = Σ n = 0 ∞ ( − 1 ) n − 1 x n n = x − x 2 2 + x 3 3 − x 4 4 + . . . ln(1+x)=\Sigma_{n=0}^{\infty}(-1)^{n-1}\frac{x^n}{n}=x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+... ln(1+x)=Σn=0∞(−1)n−1nxn=x−2x2+3x3−4x4+...
- s i n x = Σ n = 0 ∞ ( − 1 ) n x 2 n + 1 ( 2 n + 1 ) ! = x − x 3 3 ! + x 5 5 ! − x 7 7 ! + . . . sinx=\Sigma_{n=0}^{\infty}(-1)^n\frac{x^{2n+1}}{(2n+1)!}=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+... sinx=Σn=0∞(−1)n(2n+1)!x2n+1=x−3!x3+5!x5−7!x7+...
- c o s x = Σ n = 0 ∞ ( − 1 ) n x 2 n ( 2 n ) ! = x − x 2 2 ! + x 4 4 ! − x 6 6 ! + . . . cosx=\Sigma_{n=0}^{\infty}(-1)^n\frac{x^{2n}}{(2n)!}=x-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+... cosx=Σn=0∞(−1)n(2n)!x2n=x−2!x2+4!x4−6!x6+...
3. 几何应用
3.1 判断极值点的第一充分条件
设 f ( x ) 在 x = x 0 处 连 续 , 在 x 0 某 去 心 邻 域 U ( x 0 , δ ) 内 可 导 : 设f(x)在x=x_0处连续,在x_0某去心邻域U(x_0,\delta)内可导: 设f(x)在x=x0处连续,在x0某去心邻域U(x0,δ)内可导:
- a . 若 当 x ∈ ( x 0 − δ , x 0 ) 时 f ′ ( x ) < 0 , 当 x ∈ ( x 0 , x 0 + δ ) 时 f ′ ( x ) > 0 , 则 极 小 值 点 a. 若当x\in(x_0-\delta,x_0)时f'(x)<0,当x\in(x_0,x_0+\delta)时f'(x)>0,则极小值点 a.若当x∈(x0−δ,x0)时f′(x)<0,当x∈(x0,x0+δ)时f′(x)>0,则极小值点
- a . 若 当 x ∈ ( x 0 − δ , x 0 ) 时 f ′ ( x ) > 0 , 当 x ∈ ( x 0 , x 0 + δ ) 时 f ′ ( x ) < 0 , 则 极 大 值 点 a. 若当x\in(x_0-\delta,x_0)时f'(x)>0,当x\in(x_0,x_0+\delta)时f'(x)<0,则极大值点 a.若当x∈(x0−δ,x0)时f′(x)>0,当x∈(x0,x0+δ)时f′(x)<0,则极大值点
- f ′ ( x ) 在 ( x 0 − δ , x 0 ) 和 ( x 0 , x 0 + δ ) 上 不 变 号 , 则 不 是 极 值 点 f'(x)在(x_0-\delta,x_0)和(x_0,x_0+\delta)上不变号,则不是极值点 f′(x)在(x0−δ,x0)和(x0,x0+δ)上不变号,则不是极值点
3.2 判断极值点的第三充分条件(第二充分条件是三的特例)
设 f ( x ) 在 x 0 处 n 阶 可 导 , 且 f ( m ) ( x 0 ) = 0 ( m = 1 , 2 , . . . , n − 1 ) , f ( n ) ( x 0 ) ≠ 0 ( n ≥ 2 ) : 设f(x)在x_0处n阶可导,且f^{(m)}(x_0)=0(m=1,2,...,n-1),f^{(n)}(x_0)\neq0(n\geq2): 设f(x)在x0处n阶可导,且f(m)(x0)=0(m=1,2,...,n−1),f(n)(x0)=0(n≥2):
- 当 n 为 偶 数 时 且 f ( n ) ( x 0 ) < 0 , f ( x ) 在 x 0 处 取 极 大 值 当n为偶数时且f^{(n)}(x_0)<0,f(x)在x_0处取极大值 当n为偶数时且f(n)(x0)<0,f(x)在x0处取极大值
- 当 n 为 偶 数 时 且 f ( n ) ( x 0 ) > 0 , f ( x ) 在 x 0 处 取 极 小 值 当n为偶数时且f^{(n)}(x_0)>0,f(x)在x_0处取极小值 当n为偶数时且f(n)(x0)>0,f(x)在x0处取极小值
3.3 凹凸性
定 义 : f ( x 1 ) + f ( x 2 ) 2 > f ( x 1 + x 2 2 ) , 图 形 上 任 意 弧 段 位 于 弦 的 下 方 → 凹 曲 线 ; 反 之 , 凸 曲 线 。 定义:\frac{f(x_1)+f(x_2)}{2}>f(\frac{x_1+x_2}{2}),图形上任意弧段位于弦的下方\rightarrow 凹曲线;反之,凸曲线。 定义:2f(x1)+f(x2)>f(2x1+x2),图形上任意弧段位于弦的下方→凹曲线;反之,凸曲线。
充 分 条 件 : 设 函 数 f ( x ) 在 I 上 二 阶 可 导 , ( a ) 若 在 I 上 f ′ ′ ( x ) > 0 , 在 f ( x ) 在 I 上 的 图 形 是 凹 的 ; ( b ) 若 在 I 上 f ′ ′ ( x ) < 0 , 在 f ( x ) 在 I 上 的 图 形 是 凸 的 。 充分条件:设函数f(x)在I上二阶可导,(a)若在I上f''(x)>0,在f(x)在I上的图形是凹的;(b)若在I上f''(x)<0,在f(x)在I上的图形是凸的。 充分条件:设函数f(x)在I上二阶可导,(a)若在I上f′′(x)>0,在f(x)在I上的图形是凹的;(b)若在I上f′′(x)<0,在f(x)在I上的图形是凸的。
另 一 种 凹 凸 性 的 定 义 : 设 f ( x ) 在 ( a , b ) 上 连 续 , 若 对 ( a , b ) 内 任 意 两 点 x 1 , x 2 , λ ∈ ( 0 , 1 ) , 有 f [ λ x 1 + ( 1 − λ ) x 2 ] ≥ λ f ( x 1 ) + ( 1 − λ ) f ( x 2 ) , 则 称 f ( x ) 在 ( a , b ) 内 的 图 形 是 凸 的 ; 否 则 , 凹 。 另一种凹凸性的定义:设f(x)在(a,b)上连续,若对(a,b)内任意两点x_1,x_2,\lambda\in(0,1),有f[\lambda x_1+(1-\lambda)x_2]\geq\lambda f(x_1)+(1-\lambda)f(x_2),则称f(x)在(a,b)内的图形是凸的;否则,凹。 另一种凹凸性的定义:设f(x)在(a,b)上连续,若对(a,b)内任意两点x1,x2,λ∈(0,1),有f[λx1+(1−λ)x2]≥λf(x1)+(1−λ)f(x2),则称f(x)在(a,b)内的图形是凸的;否则,凹。
3.4 拐点
定义:连续曲线凹弧和凸弧的分界点。
必 要 条 件 : 设 f ′ ′ ( x 0 ) 存 在 , 且 点 ( x 0 , f ( x 0 ) ) 为 曲 线 上 的 拐 点 , 则 f ′ ′ ( x 0 ) = 0 必要条件:设f''(x_0)存在,且点(x_0,f(x_0))为曲线上的拐点,则f''(x_0)=0 必要条件:设f′′(x0)存在,且点(x0,f(x0))为曲线上的拐点,则f′′(x0)=0
第 一 充 分 条 件 : 设 f ( x ) 在 点 x = x 0 处 连 续 , 在 点 x = x 0 的 某 去 心 邻 域 U ( x 0 , δ ) 内 二 阶 导 数 存 在 , 且 在 改 点 的 左 右 邻 域 变 号 第一充分条件:设f(x)在点x=x_0处连续,在点x=x_0的某去心邻域U(x_0,\delta)内二阶导数存在,且在改点的左右邻域变号 第一充分条件:设f(x)在点x=x0处连续,在点x=x0的某去心邻域U(x0,δ)内二阶导数存在,且在改点的左右邻域变号 则 点 ( x 0 , f ( x 0 ) ) 为 曲 线 上 的 拐 点 。 则点(x_0,f(x_0))为曲线上的拐点。 则点(x0,f(x0))为曲线上的拐点。
第 三 充 分 条 件 : 设 f ( x ) 在 x 0 处 n 阶 可 导 , 且 f ( m ) ( x 0 ) = 0 ( m = 2 , . . . , n − 1 ) , f ( n ) ( x 0 ) ≠ 0 ( n ≥ 3 ) , 则 当 n 为 奇 数 时 , ( x 0 , f ( x 0 ) ) 为 拐 点 。 第三充分条件:设f(x)在x_0处n阶可导,且f^{(m)}(x_0)=0(m=2,...,n-1),f^{(n)}(x_0)\neq 0(n \geq 3),则当n为奇数时,(x_0,f(x_0))为拐点。 第三充分条件:设f(x)在x0处n阶可导,且f(m)(x0)=0(m=2,...,n−1),f(n)(x0)=0(n≥3),则当n为奇数时,(x0,f(x0))为拐点。
3.5 渐近线
斜 渐 近 线 的 定 义 : 若 l i m x → + ∞ f ( x ) x = l i m x → − ∞ f ( x ) x = k , l i m x → + ∞ [ f ( x ) − k x ] = l i m x → − ∞ [ f ( x ) − k x ] = b , 则 称 y = k x + b 是 曲 线 y = f ( x ) 的 一 条 斜 渐 近 线 。 斜渐近线的定义:若lim_{x\rightarrow +\infty}\frac{f(x)}{x}=lim_{x\rightarrow -\infty}\frac{f(x)}{x}=k,lim_{x\rightarrow +\infty}[f(x)-kx]=lim_{x\rightarrow -\infty}[f(x)-kx]=b,则称y=kx+b是曲线y=f(x)的一条斜渐近线。 斜渐近线的定义:若limx→+∞xf(x)=limx→−∞xf(x)=k,limx→+∞[f(x)−kx]=limx→−∞[f(x)−kx]=b,则称y=kx+b是曲线y=f(x)的一条斜渐近线。
3.6 作函数图形
1 ) 确 定 f ( x ) 的 定 义 域 , 判 断 奇 偶 性 ; 2 ) 求 出 f ′ ( x ) , f ′ ′ ( x ) , 用 f ( x ) 的 无 定 义 点 , f ′ ( x ) = 0 的 点 , f ′ ( x ) 不 存 在 的 点 , f ′ ′ ( x ) = 0 的 点 , f ′ ′ ( x ) 不 存 在 的 点 将 定 义 域 划 分 为 多 个 子 区 间 , 确 定 每 个 子 区 间 上 的 单 调 性 1) 确定f(x)的定义域,判断奇偶性;2) 求出f'(x),f''(x),用f(x)的无定义点,f'(x)=0的点,f'(x)不存在的点,f''(x)=0的点,f''(x)不存在的点将定义域划分为多个子区间,确定每个子区间上的单调性 1)确定f(x)的定义域,判断奇偶性;2)求出f′(x),f′′(x),用f(x)的无定义点,f′(x)=0的点,f′(x)不存在的点,f′′(x)=0的点,f′′(x)不存在的点将定义域划分为多个子区间,确定每个子区间上的单调性 , 凹 凸 性 , 得 到 极 值 点 和 拐 点 ; 3 ) 渐 近 线 。 看 一 个 例 题 : ,凹凸性,得到极值点和拐点;3)渐近线。看一个例题: ,凹凸性,得到极值点和拐点;3)渐近线。看一个例题:
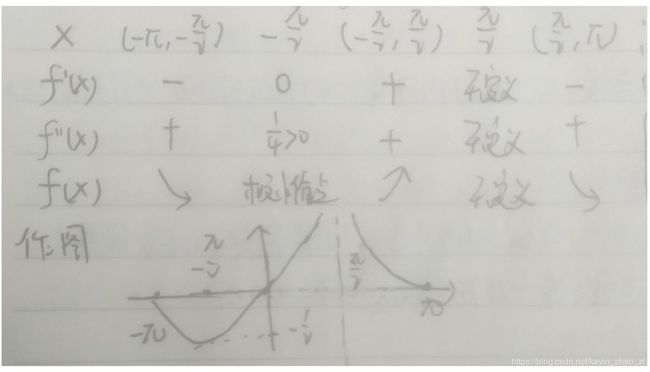
e g . 画 出 函 数 f ( x ) = s i n x 1 − s i n x 在 [ − π , π ] 上 的 图 形 。 eg.画出函数f(x)=\frac{sinx}{1-sinx}在[-\pi,\pi]上的图形。 eg.画出函数f(x)=1−sinxsinx在[−π,π]上的图形。
解 : 确 定 定 义 域 [ − π , π 2 ) ⋃ ( π 2 , π ] 解:确定定义域[-\pi,\frac{\pi}{2})\bigcup (\frac{\pi}{2},\pi] 解:确定定义域[−π,2π)⋃(2π,π]
一 阶 导 : f ′ ( x ) = c o s x ( 1 − s i n x ) 2 , 令 f ′ ( x ) = 0 , 得 x 1 = − π 2 , x 2 = π 2 ( 无 定 义 ) 一阶导:f'(x)=\frac{cosx}{(1-sinx)^2},令f'(x)=0,得x_1=-\frac{\pi}{2},x_2=\frac{\pi}{2}(无定义) 一阶导:f′(x)=(1−sinx)2cosx,令f′(x)=0,得x1=−2π,x2=2π(无定义)
二 阶 导 : f ′ ′ ( x ) = − s i n x ( 1 − s i n x ) 2 − c o s x ⋅ 2 ( 1 − s i n x ) ( − c o s x ) ( 1 − s i n x ) 4 = 1 ( 1 − s i n x ) 2 + c o s 2 x ( 1 − s i n x ) 3 , 可 知 在 区 间 ( − π , π 2 ) ⋃ ( π 2 , π ) 上 二 阶 导 数 大 于 0 , f ( − π 2 ) = − 1 2 为 极 小 值 点 ; 二阶导:f''(x)=\frac{-sinx(1-sinx)^2-cosx\cdot 2(1-sinx)(-cosx)}{(1-sinx)^4}=\frac{1}{(1-sinx)^2}+\frac{cos^2x}{(1-sinx)^3},可知在区间(-\pi,\frac{\pi}{2})\bigcup (\frac{\pi}{2},\pi)上二阶导数大于0,f(-\frac{\pi}{2})=-\frac12为极小值点; 二阶导:f′′(x)=(1−sinx)4−sinx(1−sinx)2−cosx⋅2(1−sinx)(−cosx)=(1−sinx)21+(1−sinx)3cos2x,可知在区间(−π,2π)⋃(2π,π)上二阶导数大于0,f(−2π)=−21为极小值点;
并 且 , l i m x → π 2 f ( x ) = l i m x → π 2 s i n x 1 − s i n x = + ∞ , 所 以 x = π 2 是 一 条 铅 锤 渐 近 线 。 另 外 f ( 0 ) = f ( − π ) = f ( π ) = 0 , 列 表 并 画 图 如 下 : 并且,lim_{x\rightarrow \frac{\pi}{2}}f(x)=lim_{x\rightarrow \frac{\pi}{2}}\frac{sinx}{1-sinx}=+\infty,所以x=\frac{\pi}{2}是一条铅锤渐近线。另外f(0)=f(-\pi)=f(\pi)=0,列表并画图如下: 并且,limx→2πf(x)=limx→2π1−sinxsinx=+∞,所以x=2π是一条铅锤渐近线。另外f(0)=f(−π)=f(π)=0,列表并画图如下:
欢迎扫描二维码关注微信公众号 深度学习与数学 [每天获取免费的大数据、AI等相关的学习资源、经典和最新的深度学习相关的论文研读,算法和其他互联网技能的学习,概率论、线性代数等高等数学知识的回顾]
![]()