一元多项式相加的算法和C++实现
利用顺序表的链式存储实现一元多项式的加法
一、数据结构
struct PolyNode
{
float coef; //多项式的系数
int expn; //多项式的指数
PolyNode *next; //指向下一个结点的指针
};void InitList(PolyNode *&L) //初始化多项式单链表void InsertNode(PolyNode *&L, float c, int e, int i) //在多项式链表的第i个位置插入结点void print(PolyNode *L) //打印多项式void SortList(PolyNode *&L) //按指数非递减给多项式排序void CreateList(PolyNode *&L, float C[], int E[], int n) //创建多项式单链表PolyNode *AddPoly(PolyNode *L1, PolyNode *L2) //一元多项式相加二、核心算法描述
1.创建一个空的链表,用作存储两个多项和的链表
2.调用SortList函数,给两个多项式按指数非递减的顺序给多项式排序
3.比较两个多项式链表的第一项的指数,如果链表a>b,则将较小指数的b的系数和指数复制到新建空结点s,再讲s链接到链表c的末尾;否则,换成a。如果a=b,则又分为两种情况:如果a的结点和b的结点的系数之和不为0,就将a和b的系数之和复制给s,将a或b任意一个的指数复制给s,再将s链接到c的末尾;如果为0,就跳过a和b的这两个结点,继续后面的比较。重复上述过程,知道任意一个链表为空为止。
4.如果a为空,就将b的后面部分复制给s,然后依次链接到c的末尾;如果b为空,就将a的后面部分复制给s,然后依次链接到c的末尾。
三、完整程序代码
#include "stdafx.h"
#include
using namespace std;
/*实现一元多项式的加法*/
struct PolyNode
{
float coef; //多项式的系数
int expn; //多项式的指数
PolyNode *next; //指向下一个结点的指针
};
void InitList(PolyNode *&L) //初始化多项式单链表
{
L = new PolyNode; //生成一个头结点
L->next = NULL;
}
void InsertNode(PolyNode *&L, float c, int e, int i) //在多项式链表的第i个位置插入结点
{
PolyNode *p, *q;
q = new PolyNode;
q->coef = c;
q->expn = e;
q->next = NULL;
p = L;
int j = 1;
while (j < i) //找到第i-1个结点,在它的后面插入结点
{
p = p->next;
++j;
}
q->next = p->next;
p->next = q;
}
void print(PolyNode *L) //打印多项式
{
PolyNode *p;
p = L->next;
while (p != NULL)
{
cout << "(" << p->coef <<","<expn<< ") ";
p = p->next;
}
cout << endl;
}
void SortList(PolyNode *&L) //按指数非递减给多项式排序
{
PolyNode *p, *q, *pre;
p = L->next;
L->next = NULL;
while (p != NULL)
{
if (L->next == NULL) //处理第一个结点
{
L->next = p;
p = p->next;
L->next->next = NULL;
}
else //处理剩余其他结点
{
pre = L;
q = pre->next;
while (q && q->expn < p->expn)
{
pre = q;
q = q->next;
}
q = p->next;
p->next = pre->next;
pre->next = p;
p = q;
}
}
}
void CreateList(PolyNode *&L, float C[], int E[], int n) //创建多项式单链表
{
int i;
InitList(L);
for (i = 0; i < n; i++)
{
InsertNode(L, C[i], E[i], i+1);
}
}
PolyNode *AddPoly(PolyNode *L1, PolyNode *L2) //一元多项式相加
{
PolyNode *pa, *pb, *s, *pc,*p;
PolyNode *tc; //创建尾节点
pc = new PolyNode;
pc->next = NULL; /*pc为新建单链表的头结点*/
tc = pc; /*tc始终指向新建单链表的最后结点*/
pa = L1->next;
pb = L2->next; //获得多项式单链表的第一个结点
while (pa!=NULL && pb!=NULL) //pa,pb都不为空,就进行比较,否则,跳出while
{
if (pa->expn < pb->expn) //将*pa结点复制到*s并链到pc尾
{
s = new PolyNode;
s->coef = pa->coef;
s->expn = pa->expn;
s->next = NULL;
tc->next = s;
tc = s;
pa = pa->next;
}
else if (pa->expn > pb->expn) //将*pb结点复制到*s并链到pc尾
{
s = new PolyNode;
s->coef = pb->coef;
s->expn = pb->expn;
s->next = NULL;
tc->next = s;
tc = s;
pb = pb->next;
}
else //pa->expn=pa->expn时的情况
{
if (pa->coef+pb->coef!=0) //如果相加系数之和不为0,则将新结点插在tc后面
{
s= new PolyNode;
s->coef = pa->coef + pb->coef;
s->expn = pa->expn;
s->next = NULL;
tc->next = s;
tc = s;
}
pa = pa->next; //跳过当前的结点,继续后面的结点的比较
pb = pb->next;
}
}
//将尚未扫描完的余下结点复制并链接到pc单链表之后
if (pa != NULL) //pb为空
p = pa;
else //pa为空
p = pb;
while (p != NULL)
{
s = new PolyNode;
s->coef = p->coef;
s->expn = p->expn;
s->next = NULL;
tc->next = s;
tc = s;
p = p->next;
}
return pc;
}
int main()
{
PolyNode *La, *Lb, *Lc;
float C1[] = { 3, 7, 9, 5 }, C2[] = { 8, 22, -9 };
int E1[] = { 1, 0, 8, 17 }, E2[] = { 1, 7, 8 };
InitList(La);
InitList(Lb);
InitList(Lc);
CreateList(La, C1, E1, 4);
CreateList(Lb, C2, E2, 3);
cout << "原多项式为:" << endl;
print(La);
print(Lb);
SortList(La);
SortList(Lb);
cout << "按指数非递减排序后的多项式:" << endl;
print(La);
print(Lb);
cout << "多项式相加的结果为:" << endl;
Lc = AddPoly(La,Lb);
print(Lc);
return 0;
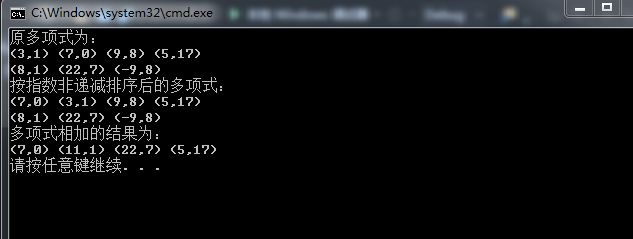
} 四、实验截图
五、总结
暑假比较闲,所以自己就想这把大二学的数据结构的一些算法全部实现一遍,分享到网上,供大家交流学习。经过差不多半天的时间吧,自己先是好好研究了单链表的各种操作特性,然后分析了怎样用单链表存储多项式,怎样实现多项式的加法的各种细节,先在草稿纸上写了大概的伪代码,然后再敲代码实现,边敲代码,边思考每行每部分的功能联系,这样既能节约时间,也能尽量减少过程的代码产生。总之,这半天的时间没白费,自己收获很多,只有亲自动手实践,才能真正懂得一个知识点的内涵。所以,我也希望看到这篇文章的同学们也多多动手,亲自去实现自己的算法,这样自己才会慢慢收获一些东西,慢慢成长。