牛客算法第二课——递归分治stl的笔记与总结
牛客算法第二课——递归分治stl的笔记与总结
一:分治
1.1. 概念:当求解某些问题时,由于数据量众多或者过程复杂导致求解过程不易实施。此时,则可将其分解成几个子问题,当求出子问题的解法后,再将其组合成整个问题的解法。(感觉类似于递归的思想,就是一个大问题的解法依赖于一个较小问题,这个较小问题又依赖于更小问题的解法,以次类推,直到小到我们可以直接求解问题)
int Fib(int n)
{
return n>=3? Fib(n-1)+Fib(n-2):1;
}感觉这个用三目运算符递归求斐波那契数列的代码写的好漂亮,作为初学者我常常只用if else 的分支语句写简单的递归。
1.2. 递归的经典例题汉诺塔问题
这道题目就是典型需要分治与递归思想,(因为正着想问题太复杂了,所以需要倒着推)
我们先来假设只有1个盘子,问题的求解就是:A->C.
假设只有2个盘子,问题的求解就是:A->B,A->C,B->C.
假设只有三个盘子,问题的求解就是:A-C,A->B,C->B,(是不是操作很像第二步,只是将B,C互换) A->C,B->A,B->C,A->C(是不是操作还是很像第二步?只是将A,B互换)
解释:当有三个盘子的时候,我们可以看成只有两个盘子,将A柱子上面的两个盘子看成一个整体,此时问题的求解就是两个盘子的解法,先将A柱子上面的两个盘子移动到B柱子上(递归第二步,只不过B,C换个顺序),再将A柱子最底下的盘子移动到C柱子上,再将B柱子的两个盘子移动到C柱子上(递归第二步,只不过A,B换个顺序)
假设有n个盘子
同理三个盘子,将A柱子上面的n-1个盘子看成一个整体,则先将这n-1个盘子移动到B柱子上(此时问题的求解变成了求n-1个盘子的汉诺塔问题,只不过是从A柱子移动到B柱子上,以次类推,形成递归),再将A柱子上的最后一个圆盘移动到C柱子,最后将B柱子上的n-1个盘子移动到C柱子上(又是一个n-1个盘子的汉诺塔问题,只不过是从B柱子移动到C柱子)
代码实现:
#include
void Move(int n,char a, char b)
{
printf("Move %d : from %c to %c\n",n,a,b); // n代表第几个盘子。 从上往下计数。
}
void Hannota(int n,char a, char b , char c)//表示从char a移动到char c的汉诺塔问题的求解
{
if(n==1) Move(n,a,c);
else
{
Hannota(n-1,a,c,b); //将上面A柱子上n-1个盘子从a移动到b
Move(n,a,c); //将A柱子最底下的最大的盘子从a移动到c
Hannota(n-1,b,a,c); //将B柱子上n-1个盘子从b移动到c;
}
}
int main()
{
printf("please input the number of disks :");
int n;
scanf("%d",&n);
Hannota(n,'a','b','c');
return 0;
}
1.3.树
1.3.1 树的概念与特点
树是一种数据结构,它是由n个有限节点组成一个具有层次关系的集合。
特点:1 每个节点有零个或多个子节点
2 没有父节点的节点称为根节点
3 每一个非根节点有且只有一个父节点,除了叶子节点外,每个子节点可以分成多个不相交的子树
二叉树:每个节点最多含有两个子树,而且每个儿子分左右
满二叉树:除最后一层无任何字节点,每一层上的所有节点都有两个子节点的二叉树
完全二叉树:除最后一层外,每一层上的节点均达到最大值,在最后一层上只缺少右边的弱干节点。
对于完全二叉树的存储(数组): 左儿子编号=根编号*2,右儿子编号=根编号*2+1, 根编号 = 儿子的编号/2。
(注意根节点编号为1,数组0的位置是空的)
1.3.2 二叉树的遍历:
先序遍历:首先访问根节点,然后遍历左子树,最后遍历右子树,在遍历左右子树的时候,仍按照根-左-右的顺序
(遍历左右子树的时候理解为递归,继续按原顺序遍历)
中序遍历:首先遍历左子树,然后遍历根节点,最后遍历右子树,在遍历左右子树的时候,仍然按照左-右-根的顺序继续遍历
(思想和前序遍历一致)
后序遍历:先遍历左子树,然后右子树,最后访问根节点,在遍历左右子树的时候,仍然按照左-右-根的顺序继续遍历
(思想和前序遍历一致)
这里的序可以理解为遍历根的顺序,先序遍历先遍历根,中序遍历在中间遍历根,后续遍历最后遍历根。
层序遍历:一层一层遍历,先访问根,再访问第一层,然后第二层...。(从上往下,从左往右)
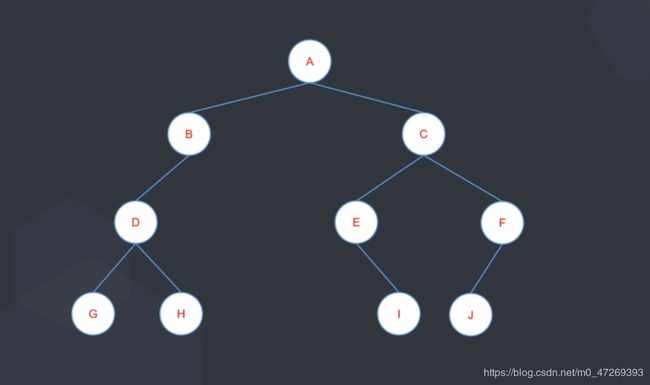
以上图为例:
前序遍历:A B D G H C E I F J
中序遍历:G D H B A E I C J F
后序遍历:G H D B I E J F C A
层序遍历:A B C D E F G H I J
1.3.3 已知前序中序求后序
已知前序遍历:ABCDFE
中序遍历为:BADFCE
关键在于找根:通过前序遍历易知 A为根
通过中序遍历,根在中间,则左子树为B,右子树为DFCE,
在对右子树进行递归操作,在前序遍历中知到C为根,则C的左子树为DF,右子树为E,再对左子树进行递归操作
在前序遍历中得知D为根。
这棵树的图形为: A
B C
D E
F
所以后序遍历为:B F D E C A
同理 这种题目的关键在于找根!
知道前序遍历和中序遍历或者后序遍历和中序遍历,树是唯一的
然而知道前序遍历和后序遍历,此时不知道根的位置,树是不唯一的。
代码实现:
#include
char q[20],z[20];
void deal(int ql,int qr,int zl, int zr) //ql-qr是遍历区间的前序遍历,zl-zr是遍历区间的中序遍历。
{
int i,root;
if(ql>qr) return ;
if(ql==qr)
{
printf("%c ",q[ql]);
return ;
}
for(i=zl;i<=zr;i++)
if(z[i]==q[ql])
{
root=i;
break;
}
deal( ql+1,ql+i-zl, zl,i-1); //要注意两处的长度要相等,前序遍历的区间长度和中序遍历的区间长度。
deal( ql+1+i-zl,qr,i+1,zr);
printf("%c ",z[i]);
}
int main()
{
int n;
printf("please input the number of roots :");
scanf("%d",&n);
printf("please input 前序遍历 :");
scanf("%s",q);
printf("please input 中序遍历 :");
scanf("%s",z);
deal(0,n-1,0,n-1);
return 0;
} 二:归并排序与快速排序
2.1 基础排序
三种O(n^2)的排序:冒泡排序,选择排序,插入排序。(都是很基础的排序)
冒泡:每次比较相邻的两个数,大的数往后。
选择:每次遍历一遍,找出最大的数和最后一个数交换。
插入:像打牌一样,每次接收到一张牌,把它插在合适的地方。
三种不基于比较的排序:桶排序(明明的随机数),基数,计数。
桶排序:例 5 4 5 5 2 2 3,利用另外一个数组b[6],其中b[i]代表i出现的次数。则b数组最后结果是
0 0 2 1 1 3,所以最后输出是 2 2 3 4 5 5 5.(缺陷能够开的最大数组大约是10^8,一旦有大于10^8的数要排序
则无法利用桶排序了)
基数排序:(桶排序的升华,解决了排不了大数的缺陷)利用多个桶来排序
例如:43 45 41 23 21 71.
第一个桶来排个位: 个位为 1 : 41 21 71 第二个桶来排十位: 十位为2:21 23
个位为3 : 43 23 十位为4: 41 43 45
个位为5: 45 十位为7:71
计数排序:(还是桶排序的升华)基于桶排序,进行了一次前缀和。
b[i]代表i有多少个,那么前缀和则是<=i的数共有多少个。 那么当插入x的时候,就知道x排在第几个。
例:sum[x]=15,sum[x-1]=5,那么就知道等于x的数有5个,且x该排在第几位。
2.2 归并排序与快速排序
归并排序:每次将待排序区间一分为二,将两个子区间排序(进行递归,再进行归并排序),然后将两个已经排好序的序列合并。(时间复杂度n*logn)
快速排序:选择一个基准,将小于基准的放在基准左边,大于基准的放在基准右边,然后对基准左右都继续执行如上操作直到全部有序(时间复杂度平均=n*logn,最差的情况是n^2).
C++中sort的时间复杂度是严格n*logn;
归并排序代码实现如下:
#include
int a[101],b[101];
void merge(int l,int mid,int r)
{
int p1=l,p2=mid+1;
int i=l;
while(p1<=mid&&p2<=r)
if(a[p1]l)
{
erfen(l,mid);
erfen(mid+1,r);
}
merge(l,mid,r);
}
int main()
{
printf("please input the number of digits (n<=100):");
int n;
scanf("%d",&n);
int i;
printf("please input the digits of sort :");
for(i=1;i<=n;i++)
scanf("%d",&a[i]);
erfen(1,n);
for(i=1;i<=n;i++)
printf("%d ",a[i]);
return 0;
} 快速排序的代码实现如下:(基准找的是中间的数)
void quick_sort(int l,int r)
{
int i=l,j=r;
int mid=(l+r)/2;
int x=a[mid];
while(i<=j)
{
while(a[i]x) j--;
if(i 我自己对快速排序的思想感觉没怎么懂,这里的用另外一个变量x存储a[mid]的道理我懂了,但整体代码感觉好精妙,可能自己还要再参悟几天吧。
2.3 求逆序对个数
猫猫 TOM 和小老鼠 JERRY 最近又较量上了,但是毕竟都是成年人,他们已经不喜欢再玩那种你追我赶的游戏,现在他们喜欢玩统计。
最近,TOM 老猫查阅到一个人类称之为“逆序对”的东西,这东西是这样定义的:对于给定的一段正整数序列,逆序对就是序列中 ai>aj 且 i Update:数据已加强。 第一行,一个数 n,表示序列中有 n个数。 第二行 n 个数,表示给定的序列。序列中每个数字不超过 10^9。 输出序列中逆序对的数目。 输入 #1 输出 #1 对于 25% 的数据,n≤2500 对于 50% 的数据,n≤4×10^4。 对于所有数据,n≤5×10^5 请使用较快的输入输出 应该不会 O(n2) 过 50 万吧 思路一:我一开始的想法是用冒泡排序,每次冒泡交换的个数就是逆序对,所以只需在swap中加个计数就可以了,代码简单。 但显然,这种代码在这样的大数据下肯定会limit.(时间复杂度是O(n^2)的一般都过不了) 结果在洛谷上只得了25分。 思路二:用归并排序,此处就要注意在归并排序中何处消去了逆序对,消去了几个逆序对 代码实现如下 2.4:求一个序列的第K大数(数字个数<=10^8) 应用快排,但我不会!!!!!!(快排我还没看懂) 2.5:求最大字串和 将数组二分,则最大字串分为三种情况, 一.最大字串的两端全部在左半区间 二.最大字串的两端全部在右半区间 三.最大字串的两端一端在左半区间,一端在右半区间 代码实现(比较这三段最大字串) 三:STL(第一次听说,刚学c的小白从来没遇到过)(c语言中没有,没学过c++,就不冒昧地整理了) 3.1: 栈:仅在表头进行插入和删除操作的线性表(先进后出) 队列:队列是一种特殊的链表,特殊之处在于只允许在表的前端进行删除操作,而在表的后端进行插入操作,和栈一样,队列是一种操作受限制的线性表,进行插入操作的端称为队尾,进行删除操作的端称为队头。(先进先出) 可以用数组或者链表来实现对栈和队列的存储和一些操作。(在数据结构与算法课程中将会学到,但我自学的数据结构与算法的编程基础有点差) 3.1.1 有n个人,按照1,2,3,4...n的顺序依次进栈,判断出栈顺序(重点在于判断栈顶元素与要出栈元素是否相等) 代码以后补充,对于栈的数据结构的c语言操作我还掌握的不熟练。 3.2 map *map内部使用平衡二叉树实现 *理解为“自定义下标的数组” *实际上有序 我第一次接触这个东西,我的理解是数组的下标被扩展成各种各样的,而不仅仅是int,例a[“score”]=10,数组下标是个字符串。 。。。。。。。。。。。。。。。。。。。。。。。。 再往下的知识点和代码就都超出了我的能力范围了,涉及太多C++的知识,还没有接触C++的我有点困难。 总结一下: 1. 我以前觉得把算法变成代码比较困难,但经过本节课 我实际编码了一下才发觉写代码是最简单的事情。要理清思路和算法才是重点. 2.debug是一种能力,只有学会调试才能找出错误,写出高质量的代码。(但可惜,目前我的调试能力还很差,一旦遇到很难调试的代码比如递归等,我比较无奈) 3.写完代码,提交成功后要写注释,要规范代码,比如缩进,简化等,一般经过这一步后,代码才能变得好看,精简。 吐槽几句:大一下学期过的比较荒废,可能由于学习不感兴趣的课程吧,课业没怎么学习,写代码可能有了长进,可还是难以应付BUPT的转专业考试(竟然大多数涉及大二学习的数据结构与算法),感觉自己整个人在家里都是废的这学期,只希望快点开学,快点感受来自同校师生的压力。 输入格式
输出格式
输入输出样例
6
5 4 2 6 3 111说明/提示
#include#includeint maxs(int n,int l,int r)
{
int mid=(l+r)/2;
if(l==r) return a[l];
int ans= max(maxs(n,l,mid),maxs(n,mid+1,r)); //ans是左右区间的连续最大子列和
int ll=0,rr=0,temp=0;
int i;
int tmp=0;
for(i=mid+1;i<=r;i++)
{
temp+=a[i];
rr=max(rr,temp);
}
temp=0;
for(i=mid;i>=1;i--)
{
temp+=a[i];
ll=max(ll,temp);
}
ans=max(ans,ll+rr); //比较左右区间的连续最大子列和和中间的连续最大子列和
return ans;
}