树状数组

一、概述

1、求区间元素和、修改某个位置的值 O(logn)
2、常数小于线段树，代码更短
3、应用范围比线段树广

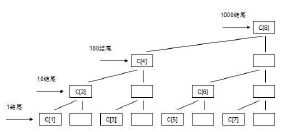
二、构建

满二叉树，C[i]为A[i]对应的那一列的最高的节点

C[1]=A[1];
C[2]=A[1]+A[2];
C[3]=A[3];
C[4]=A[1]+A[2]+A[3]+A[4];
C[5]=A[5];
C[6]=A[5]+A[6];
C[7]=A[7];
C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];

十进制转化为二进制：
1 00000001
2 00000010
3 00000011
4 00000100
5 00000101
6 00000110
7 00000111
8 00001000

注意每种结尾中0的个数：
以1结尾的节点C[i]代表A[i]，表示的区间长度为1(2^0)
以10结尾的节点C[i]代表A[i]+A[i-1]，表示的区间长度为2(2^1)
以100结尾的节点C[i]代表A[i]+A[i-1]+A[i-2]+A[i-3]，表示的区间长度为4(2^2)
以1000结尾的节点C[i]代表A[i]+A[i-1]+A[i-2]+A[i-3]+A[i-4]+A[i-5]+A[i-6]+A[i-7]，表示的区间长度为8(2^3)

因此可以扩展归纳为：如果i的二进制中从最低位开始向最高位数有连续的x个0，那么C[i]拥有2^x个叶子?，表示的区间范围为A[i]~A[i-2^x+1]

三、求和
返回前i个元素的和

返回前i个元素的和
int Sum(int i){
	int s=0;
	while(i>0){
		s+=C[i];
		i-=i&(-i);
	}
	return s;
}

四、更新数组

将A[i]的值改为value

void Update(int i,int value){
	while(i<=n){
		C[i]+=value;
		i+=i&(-i);
	}
}

五、
1.【洛谷】P3374 【模板】树状数组 1

#include
using namespace std;
int C[500006],N,M;
void Update(int i,int value){
	while(i<=N){
		C[i]+=value;
		i+=i&(-i);
	}
}
int Sum(int i){
	int s=0;
	while(i>0){
		s+=C[i];
		i-=i&(-i);
	}
	return s;
}
int main(int argc, char const *argv[])
{
	scanf("%d%d",&N,&M);
	int number,cz,x,y;
	for(int i=1;i<=N;++i) {scanf("%d",&number);Update(i,number);}
	for(int i=1;i<=M;++i) {
		scanf("%d",&cz);
		if(cz>>1){
			scanf("%d%d",&x,&y);
			printf("%d\n",Sum(y)-Sum(x-1));
		}
		else{
			scanf("%d%d",&x,&y);
			Update(x,y);
		}
	}
	return 0;
}

2.【洛谷】P3368 【模板】树状数组 2

方法一、

在树状数组1中，Update操作会将从i之后的前i个元素和、前i+1个元素和······前N个元素和发生改变。在树状数组2中为了保证修改从x~y范围内的每一项而不影响后面项，通过Update(y+1,-k)来抵消对之后的影响（把多增加的再减回去）

#include
using namespace std;
int C[1926081],N,M;
int Sum(int i){
	int s=0;
	while(i>0){
		s+=C[i];
		i-=i&(-i);
	}
	return s;
}
void Update(int i,int value){
	while(i<=N){
		C[i]+=value;
		i+=i&(-i);
	}
}
int main(){
	scanf("%d%d",&N,&M);
	int number,cz,x,y,k;
	for(int i=1;i<=N;++i){scanf("%d",&number);Update(i,number);Update(i+1,-number);}
	for(int i=1;i<=M;++i){
		scanf("%d",&cz);
		if(cz==2){
			scanf("%d",&x);
			printf("%d\n",Sum(x));
		}
		else{
			scanf("%d%d%d",&x,&y,&k);
			Update(x,k);Update(y+1,-k);
		}
	}
	return 0;
}

方法二、

树状数组+差分：
开两个数组：a[],C[]。a[]存原来的数，C[]用于差分。存入C[]时用Update(i,a[i]-a[i-1]);
树状数组中前i个数的和表示第i个数
修改x~y区间时只需在树状数组中将x+k，y+1-k即可
询问第i个数时直接用Sum(i)输出

#include
using namespace std;
int C[7180629],a[1926081],N,M;
void Update(int i,int k){
	while(i<=N){
		C[i]+=k;
		i+=i&(-i);
	}
}
int Sum(int i){
	int s=0;
	while(i>0){
		s+=C[i];
		i-=i&(-i);
	}
	return s;
}
int main(){
	int cz,x,y,k;
	scanf("%d%d",&N,&M);
	for(int i=1;i<=N;++i){
		scanf("%d",&a[i]);
		Update(i,a[i]-a[i-1]);
	}
	for(int i=1;i<=M;++i){
		scanf("%d",&cz);
		if(cz==1){
			scanf("%d%d%d",&x,&y,&k);
			Update(x,k);
			Update(y+1,-k);
		}
		else{
			scanf("%d",&x);
			printf("%d\n",Sum(x));
		}
	}
	return 0;
}