Task1:随机事件与随机变量
阅读小助手
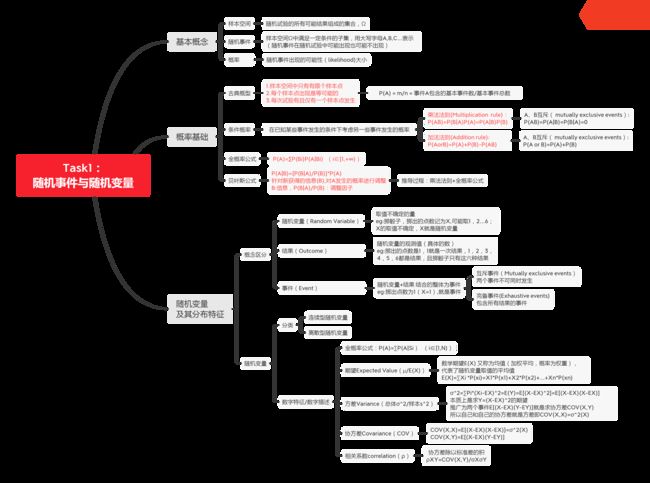
- 框架思维导图
- 一、基本概念
- 二、概率基础
- 1、古典概型
- 2、条件概率
- 3、全概率公式
- 4、贝叶斯公式—— B a y e ′ s F o r m u l a Baye's Formula Baye′sFormula
- 三、随机变量及其分布特征
- 0、随机变量分类
- 1、期望Expected Value(μ/E(X))
- 2、方差Variance(总体 σ 2 / 样 本 s 2 σ^2/样本s^2 σ2/样本s2)
- 3、协方差Covariance(COV)
- 4、相关系数correlation(ρ)
框架思维导图
一、基本概念
① 样本空间:随机试验的所有可能结果组成的集合, Ω \Omega Ω
② 随机事件:样本空间Ω中满足一定条件的子集,用大写字母 A , B , C . . . A,B,C... A,B,C...表示
(随机事件在随机试验中可能出现也可能不出现)
③ 随机变量(Random Variable):取值不确定的量
eg:掷骰子,掷出的点数记为X,可能取1,2…6;
X的取值不确定,X就是随机变量
④ 结果(Outcome):随机变量的观测值(具体的数)
eg:掷出的点数是1,1就是一次结果,1,2,3,4,5,6都是结果,
且掷骰子只有这六种结果
⑤ 事件(Event):随机变量+结果 结合的整体为事件
eg:掷出点数为1(X=1),就是事件
⑥ 互斥事件(Mutually exclusive events):两个事件不可同时发生
⑦ 完备事件(Exhaustive events):包含所有结果的事件.
⑧ 概率:随机事件出现的可能性(likelihood)大小
二、概率基础
1、古典概型
概念:
① 样本空间中只有有限个样本点
② 每个样本点出现是等可能的
③ 每次试验有且仅有一个样本点发生
P ( A ) = m n = 事 件 A 包 含 的 基 本 事 件 数 基 本 事 件 总 数 P(A)=\frac{m} {n}=\frac{事件A包含的基本事件数} {基本事件总数} P(A)=nm=基本事件总数事件A包含的基本事件数
案例1:
假设有 k k k 个不同颜色的球,每个球以同样的概率 1 / l 1/l 1/l 落到 l l l 个格子 ( l > = k ) (l>=k) (l>=k) 的每个中,且每个格子可容纳任意多个球。问,分别求出如下两个事件 A A A 和 B B B 的概率。
A A A :指定的 k k k 个格子中各有一个球;
B B B :存在 k k k 个格子,其中各有一个球。
我们思考一下,由于每个球可以平均地落入 l l l 个格子中的任一个,并且每一个格子中可落入任意多个球,所以 k k k 个球落入 l l l 个格子中的分布情况相当于从 l l l 个格子中选取 k k k 个的可重复排列,故样本空间共有 l k l^k lk 种等可能的基本结果。
所以,事件 A A A 所含基本结果数应是 k k k 个球在指定的 l l l 个格子中的全排列数,即 k ! k! k!,那么有
P ( A ) = k ! l k P(A) = \frac{k!} {l^k} P(A)=lkk!
为了算出事件 B B B 所含的基本事件数,我们可以分两步进行:
1)因为 l l l 个格子可以是任意选取的,故可先从 l l l 个格子中任意选出 k k k 个出来,那么选法共有 C l k C^k_l Clk 种。
2)对于每种选定的 k k k 个格子,依上述各有一个球的推理,则有 k ! k! k!个基本结果,故B含有 C l k ∗ k ! C^k_l*k! Clk∗k! 个基本结果。那么有
P ( B ) = C l k k ! l k = l ! l k ( l − k ) ! P(B) = \frac {C^k_lk!} {l^k} = \frac {l!} {l^k(l-k)!} P(B)=lkClkk!=lk(l−k)!l!
生日问题:求 k k k 个同班同学没有两人生日相同的概率。
如果把这 k k k 个同学看作上例中的 k k k 个球,而把一年365天看作格子,
即 l = 365 l=365 l=365 ,则上述的 P ( B ) P(B) P(B)就是所要求的概率。
令 k = 40 k=40 k=40 时,利用上面的公式,则 P ( B ) = 0.109 P(B) =0.109 P(B)=0.109。
即:40个同学中至少两个人同一天过生日的概率是:
P ( B ‾ ) = 1 − 0.109 = 0.891 P(\overline {B}) = 1 - 0.109 =0.891 P(B)=1−0.109=0.891。
Python实现:
#采用函数的递归的方法定义阶乘函数:
def factorial(n):
if n == 0:
return 1;
else:
return (n*factorial(n-1))
#也可以直接导包
from math import factorial
l_fac = factorial(365); #l的阶乘
l_k_fac = factorial(365-40) #l-k的阶乘
l_k_exp = 365**40 #l的k次方
P_B = l_fac /(l_k_fac * l_k_exp) #P(B)
print("事件B的概率为:",P_B)
print("40个同学中至少两个人同一天过生日的概率是:",1 - P_B)
2、条件概率
定义:
设 A A A 和 B B B 是两个事件,且 P ( B ) > 0 P(B)>0 P(B)>0,称 P ( B ∣ A ) = P ( A B ) P ( A ) P(B|A)=\frac{P(AB)}{P(A)} P(B∣A)=P(A)P(AB)为
在事件 A A A 发生的条件下,事件 B B B 发生的概率。
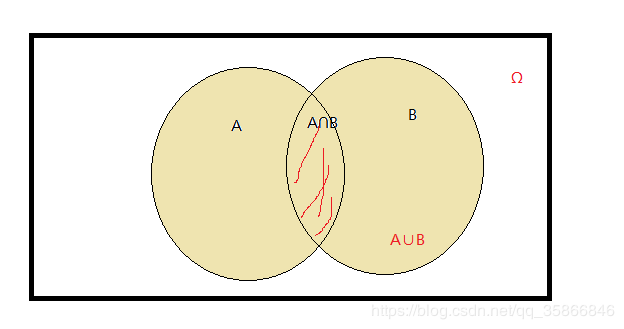
乘法法则(Multiplication rule):
P ( A B ) = P ( A ∩ B ) = P ( B ∣ A ) P ( A ) = P ( A ∣ B ) P ( B ) P(AB)=P(A∩B)=P(B|A)P(A)=P(A|B)P(B) P(AB)=P(A∩B)=P(B∣A)P(A)=P(A∣B)P(B)
当 A A A和 B B B互斥(mutually exclusive)时:
P ( A B ) = P ( A ∣ B ) = P ( B ∣ A ) = 0 P(AB)=P(A|B)=P(B|A)=0 P(AB)=P(A∣B)=P(B∣A)=0
加法法则(Addition rule):
P ( A o r B ) = P ( A ∪ B ) = P ( A ) + P ( B ) − P ( A B ) P(AorB)=P(A∪B)=P(A)+P(B)-P(AB) P(AorB)=P(A∪B)=P(A)+P(B)−P(AB)
当 A A A和 B B B互斥(mutually exclusive)时:
P ( A o r B ) = P ( A ) + P ( B ) P(AorB)=P(A)+P(B) P(AorB)=P(A)+P(B)
两个重要结论——充要条件:
互为充要条件: A 、 B 互 斥 ⟺ P ( A B ) = 0 A、B互斥 \Longleftrightarrow P(AB)=0 A、B互斥⟺P(AB)=0
互为充要条件: A 、 B 独 立 ⟺ P ( A B ) = P ( A ) ∗ P ( B ) A、B独立 \Longleftrightarrow P(AB)=P(A)*P(B) A、B独立⟺P(AB)=P(A)∗P(B)
互斥一定不独立
3、全概率公式
A 自 顾 自 发 生 的 无 条 件 概 率 P ( A ) A 自顾自发生的无条件概率P(A) A自顾自发生的无条件概率P(A) :
P ( A ) = P ( A ∣ S 1 ) ∗ P ( S 1 ) + P ( A ∣ S 2 ) ∗ P ( S 2 ) + . . . + P ( A ∣ S n ) ∗ P ( S n ) P(A)=P(A|S1)*P(S1)+P(A|S2)*P(S2)+...+P(A|Sn)*P(Sn) P(A)=P(A∣S1)∗P(S1)+P(A∣S2)∗P(S2)+...+P(A∣Sn)∗P(Sn)
其中: S 1 , S 2 , . . . S n 完 备 Ω , 且 两 两 互 斥 {S1,S2,...Sn}完备\Omega,且两两互斥 S1,S2,...Sn完备Ω,且两两互斥
推导过程:
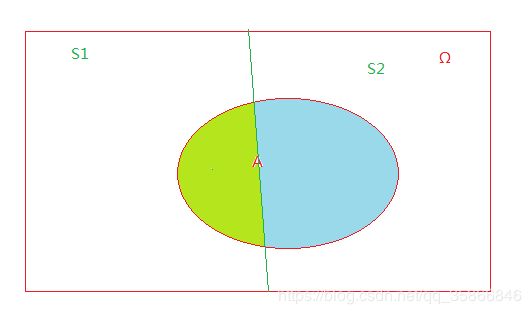
如上图: P ( S 1 ) + P ( S 2 ) = P ( Ω ) = 1 , P ( S 1 S 2 ) = 0 P(S1)+P(S2)=P(\Omega)=1,P(S1S2)=0 P(S1)+P(S2)=P(Ω)=1,P(S1S2)=0
即: S 1 , S 2 完 备 且 互 斥 {S1,S2}完备且互斥 S1,S2完备且互斥
P ( A ) = P ( 浅 绿 ) + P ( 浅 蓝 ) P(A)=P(浅绿)+P(浅蓝) P(A)=P(浅绿)+P(浅蓝) ①
P ( 浅 绿 ) = P ( A S 1 ) = P ( A ) ∗ P ( S 1 ∣ A ) P(浅绿)=P(AS1)=P(A)*P(S1|A) P(浅绿)=P(AS1)=P(A)∗P(S1∣A) ②
P ( 浅 绿 ) = P ( A S 1 ) = P ( S 1 ) ∗ P ( A ∣ S 1 ) P(浅绿)=P(AS1)=P(S1)*P(A|S1) P(浅绿)=P(AS1)=P(S1)∗P(A∣S1) ③
因为要求 P ( A ) P(A) P(A), P ( A ) P(A) P(A) 未知,所以选择③式
同理: P ( 浅 蓝 ) = P ( A S 2 ) = P ( S 2 ) ∗ P ( A ∣ S 2 ) P(浅蓝)=P(AS2)=P(S2)*P(A|S2) P(浅蓝)=P(AS2)=P(S2)∗P(A∣S2) ④
把③、④式带入①式得:
P ( A ) = P ( 浅 绿 ) + P ( 浅 蓝 ) P(A)=P(浅绿)+P(浅蓝) P(A)=P(浅绿)+P(浅蓝)
= P ( A S 1 ) + P ( A S 2 ) =P(AS1)+P(AS2) =P(AS1)+P(AS2)
= P ( S 1 ) ∗ P ( A ∣ S 1 ) + P ( S 2 ) ∗ P ( A ∣ S 2 ) =P(S1)*P(A|S1)+P(S2)*P(A|S2) =P(S1)∗P(A∣S1)+P(S2)∗P(A∣S2)
推广到 n n n 个事件,即把 Ω \Omega Ω 切分成 n n n 个 S S S 事件得:
P ( A ) = P ( A ∣ S 1 ) ∗ P ( S 1 ) + P ( A ∣ S 2 ) ∗ P ( S 2 ) + . . . + P ( A ∣ S n ) ∗ P ( S n ) P(A)=P(A|S1)*P(S1)+P(A|S2)*P(S2)+...+P(A|Sn)*P(Sn) P(A)=P(A∣S1)∗P(S1)+P(A∣S2)∗P(S2)+...+P(A∣Sn)∗P(Sn)
4、贝叶斯公式—— B a y e ′ s F o r m u l a Baye's Formula Baye′sFormula
P ( A ∣ B ) = P ( B ∣ A ) P ( B ) ∗ P ( A ) P(A|B)= \frac {P(B|A)}{P(B)}*P(A) P(A∣B)=P(B)P(B∣A)∗P(A)
针 对 新 获 得 的 信 息 ( B ) , 对 A 发 生 的 概 率 进 行 调 整 针对新获得的信息(B),对A发生的概率进行调整 针对新获得的信息(B),对A发生的概率进行调整
B : 信 息 , P ( B ∣ A ) P ( B ) : 信 息 调 整 因 子 B:信息,\frac {P(B|A)}{P(B)}:信息调整因子 B:信息,P(B)P(B∣A):信息调整因子
推导过程:
乘 法 法 则 + 全 概 率 公 式 ⟹ B a y e ′ s F o r m u l a 乘法法则+全概率公式 \Longrightarrow Baye's Formula 乘法法则+全概率公式⟹Baye′sFormula
P ( A B ) = P ( A ) ∗ P ( B ∣ A ) P(AB)=P(A)*P(B|A) P(AB)=P(A)∗P(B∣A) ①
P ( A B ) = P ( B ) ∗ P ( A ∣ B ) P(AB)=P(B)*P(A|B) P(AB)=P(B)∗P(A∣B) ②
由②得:
P ( A ∣ B ) = P ( A B ) P ( B ) P(A|B)=\frac{P(AB)}{P(B)} P(A∣B)=P(B)P(AB)
代入①得: = P ( A ) ∗ P ( B ∣ A ) P ( B ) =\frac{P(A)*P(B|A)}{P(B)} =P(B)P(A)∗P(B∣A)
⟹ P ( A ∣ B ) = P ( A ) ∗ P ( B ∣ A ) P ( B ) \Longrightarrow P(A|B)=P(A)*\frac{P(B|A)}{P(B)} ⟹P(A∣B)=P(A)∗P(B)P(B∣A)
B : 信 息 , P ( B ∣ A ) P ( B ) : 信 息 调 整 因 子 B:信息,\frac {P(B|A)}{P(B)}:信息调整因子 B:信息,P(B)P(B∣A):信息调整因子
其中
P ( B ) = P ( B ∣ S 1 ) ∗ P ( S 1 ) + P ( B ∣ S 2 ) ∗ P ( S 2 ) + . . . + P ( B ∣ S n ) ∗ P ( S n ) P(B)=P(B|S1)*P(S1)+P(B|S2)*P(S2)+...+P(B|Sn)*P(Sn) P(B)=P(B∣S1)∗P(S1)+P(B∣S2)∗P(S2)+...+P(B∣Sn)∗P(Sn)
树状图计算—— B a y e ′ s F o r m u l a 简 单 运 用 Baye's Formula 简单运用 Baye′sFormula简单运用
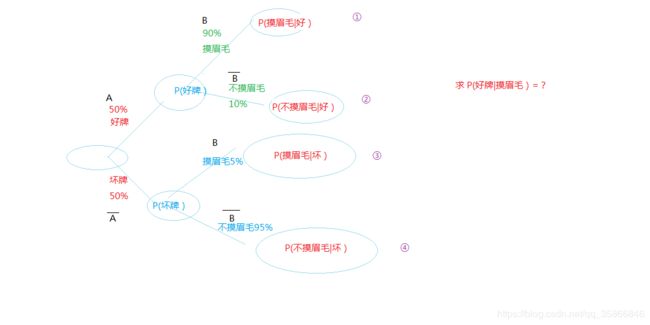
假设:
B ( 条 件 / 信 息 ) : 摸 眉 毛 ; A ( 事 件 ) : 好 牌 ⟹ 求 : P ( A ∣ B ) = ? B(条件/信息):摸眉毛;A(事件):好牌\Longrightarrow 求:P(A|B)=? B(条件/信息):摸眉毛;A(事件):好牌⟹求:P(A∣B)=?
P ( A ∣ B ) = A B P ( B ) = ① ① + ③ = 0.5 ∗ 0.9 0.5 ∗ 0.9 + 0.5 ∗ 0.05 = 0.95 P(A|B)=\frac{AB}{P(B)}=\frac{①}{①+③}=\frac{0.5*0.9}{0.5*0.9+0.5*0.05}=0.95 P(A∣B)=P(B)AB=①+③①=0.5∗0.9+0.5∗0.050.5∗0.9=0.95
三、随机变量及其分布特征
0、随机变量分类
连续型随机变量和离散性随机变量
1、期望Expected Value(μ/E(X))
数学期望E(X) 又称为均值(加权平均,概率为权重),
代表了随机变量取值的平均值
E ( X ) = Σ X i ∗ P ( x i ) = X 1 ∗ P ( x 1 ) + X 2 ∗ P ( x 2 ) + . . . + X n ∗ P ( x n ) E(X)=\Sigma Xi *P(xi)=X1*P(x1)+X2*P(x2)+...+Xn*P(xn) E(X)=ΣXi∗P(xi)=X1∗P(x1)+X2∗P(x2)+...+Xn∗P(xn)
2、方差Variance(总体 σ 2 / 样 本 s 2 σ^2/样本s^2 σ2/样本s2)
σ 2 = Σ P i ∗ ( X i − E X ) 2 σ^2=\Sigma Pi*(Xi-EX)^2 σ2=ΣPi∗(Xi−EX)2
= E ( Y ) = E [ ( X − E X ) 2 ] =E(Y)=E[(X-EX)^2] =E(Y)=E[(X−EX)2]
= E [ ( X − E X ) ( X − E X ) ] =E[(X-EX)(X-EX)] =E[(X−EX)(X−EX)]
本质上是求 Y = ( X − E X ) 2 Y=(X-EX)^2 Y=(X−EX)2的期望
推广为两个事件 E [ ( X − E X ) ( Y − E Y ) ] E[(X-EX)(Y-EY)] E[(X−EX)(Y−EY)]就是求协方差 C O V ( X , Y ) COV(X,Y) COV(X,Y)
所以自己和自己的协方差就是方差即 C O V ( X , X ) = σ 2 ( X ) COV(X,X)=σ^2(X) COV(X,X)=σ2(X)
3、协方差Covariance(COV)
C O V ( X , X ) = E [ ( X − E X ) ( X − E X ) ] = σ 2 ( X ) COV(X,X)=E[(X-EX)(X-EX)]=σ^2(X) COV(X,X)=E[(X−EX)(X−EX)]=σ2(X)
C O V ( X , Y ) = E [ ( X − E X ) ( Y − E Y ) ] COV(X,Y)=E[(X-EX)(Y-EY)] COV(X,Y)=E[(X−EX)(Y−EY)]
实际计算:——联合概率分布表
| B 1 = 0.40 B1=0.40 B1=0.40 | B 2 = 0.20 B2=0.20 B2=0.20 | B 3 = 0.00 B3=0.00 B3=0.00 | |
|---|---|---|---|
| A 1 = 0.20 A1=0.20 A1=0.20 | 0.15 | 0 | 0 |
| A 2 = 0.15 A2=0.15 A2=0.15 | 0 | 0.60 | 0 |
| A 3 = 0.04 A3=0.04 A3=0.04 | 0 | 0 | 0.25 |
E ( B ) = 0.15 ∗ 0.4 + 0.6 ∗ 0.20 + 0.25 ∗ 0 = 0.18 E(B)=0.15*0.4+0.6*0.20+0.25*0=0.18 E(B)=0.15∗0.4+0.6∗0.20+0.25∗0=0.18
E ( A ) = 0.15 ∗ 0.2 + 0.6 ∗ 0.15 + 0.25 ∗ 0.04 = 0.13 E(A)=0.15*0.2+0.6*0.15+0.25*0.04=0.13 E(A)=0.15∗0.2+0.6∗0.15+0.25∗0.04=0.13
C O V ( A , B ) = E [ ( A − E ( A ) ( B − E ( B ) ] COV(A,B)=E[(A-E(A)(B-E(B)] COV(A,B)=E[(A−E(A)(B−E(B)]
= Σ P ∗ [ A − E ( A ) ] ∗ [ B − E ( B ) ] =\Sigma P*[A-E(A)]*[B-E(B)] =ΣP∗[A−E(A)]∗[B−E(B)]
= 0.15 ∗ ( 0.20 − 0.13 ) ∗ ( 0.40 − 0.18 ) + 0.60 ∗ ( 0.15 − 0.13 ) ∗ ( 0.20 − 0.18 ) + 0.25 ∗ ( 0.04 − 0.13 ) ∗ ( 0.00 − 0.18 ) =0.15*(0.20-0.13)*(0.40-0.18)+0.60*(0.15-0.13)*(0.20-0.18)+0.25*(0.04-0.13)*(0.00-0.18) =0.15∗(0.20−0.13)∗(0.40−0.18)+0.60∗(0.15−0.13)∗(0.20−0.18)+0.25∗(0.04−0.13)∗(0.00−0.18)
= 0.0066 =0.0066 =0.0066
4、相关系数correlation(ρ)
相关系数=协方差除以标准差的积
ρ X Y = C O V ( X , Y ) σ 2 X σ 2 Y = = C O V ( X , Y ) σ X σ Y \rho XY=\frac{COV(X,Y)}{\sqrt{\sigma^2 X \sigma^2 Y}}==\frac{COV(X,Y)}{\sigma X \sigma Y} ρXY=σ2Xσ2YCOV(X,Y)==σXσYCOV(X,Y)
python实现
#导入包
import pandas as pd
import numpy as np
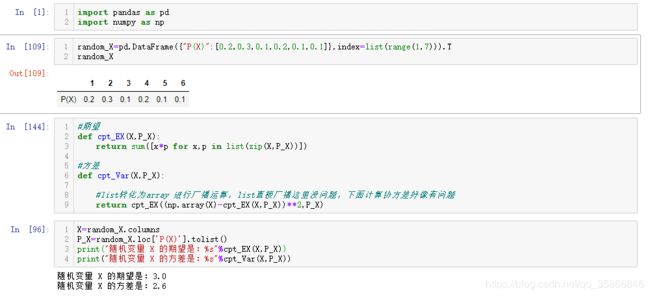
#构造单个随机变量
random_X=pd.DataFrame({"P(X)":[0.2,0.3,0.1,0.2,0.1,0.1]},index=list(range(1,7))).T
random_X
#定义期望、方差计算函数
#期望
def cpt_EX(X,P_X):
return sum([x*p for x,p in list(zip(X,P_X))])
#方差
def cpt_Var(X,P_X):
#list转化为array 进行广播运算,list直接广播这里没问题,下面计算协方差好像有问题
return cpt_EX((np.array(X)-cpt_EX(X,P_X))**2,P_X)
X=random_X.columns
P_X=random_X.loc['P(X)'].tolist()
print("随机变量 X 的期望是:%s"%cpt_EX(X,P_X))
print("随机变量 X 的方差是:%s"%cpt_Var(X,P_X))
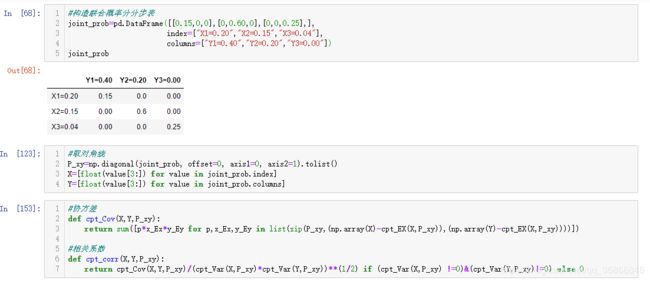
#构造联合概率分分步表
joint_prob=pd.DataFrame([[0.15,0,0],[0,0.60,0],[0,0,0.25],],
index=["X1=0.20","X2=0.15","X3=0.04"],
columns=["Y1=0.40","Y2=0.20","Y3=0.00"])
joint_prob
#取对角线
P_xy=np.diagonal(joint_prob, offset=0, axis1=0, axis2=1).tolist()
X=[float(value[3:]) for value in joint_prob.index]
Y=[float(value[3:]) for value in joint_prob.columns]
#定义协方差、相关系数计算函数
#协方差
def cpt_Cov(X,Y,P_xy):
return sum([p*x_Ex*y_Ey for p,x_Ex,y_Ey in list(zip(P_xy,(np.array(X)-cpt_EX(X,P_xy)),(np.array(Y)-cpt_EX(X,P_xy))))])
#相关系数
def cpt_corr(X,Y,P_xy):
return cpt_Cov(X,Y,P_xy)/(cpt_Var(X,P_xy)*cpt_Var(Y,P_xy))**(1/2) if (cpt_Var(X,P_xy) !=0)&(cpt_Var(Y,P_xy)!=0) else 0
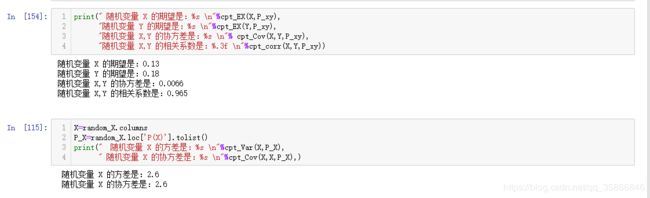
print(" 随机变量 X 的期望是:%s \n"%cpt_EX(X,P_xy),
"随机变量 Y 的期望是:%s \n"%cpt_EX(Y,P_xy),
"随机变量 X,Y 的协方差是:%s \n"% cpt_Cov(X,Y,P_xy),
"随机变量 X,Y 的相关系数是:%.3f \n"%cpt_corr(X,Y,P_xy))
#验证自己与自己的协方差等于方差
X=random_X.columns
P_X=random_X.loc['P(X)'].tolist()
print(" 随机变量 X 的方差是:%s \n"%cpt_Var(X,P_X),
" 随机变量 X 的协方差是:%s \n"%cpt_Cov(X,X,P_X),)
参看资料:
Datawhale开源-概率统计
numpy 取出对角线元素、计算对角线元素和 np.diagonal