深度立体匹配中的自监督学习概览
欢迎关注知乎专栏 双目立体匹配
深度学习的蓬勃发展得益于大规模有标注的数据驱动,有监督学习(supervised learning)推动深度模型向着性能越来越高的方向发展。但是,大量的标注数据往往需要付出巨大的人力成本,越来越多的研究开始关注如何在不获取数据标签的条件下提升模型的性能,也就是自监督学习(self-supervised learning)/无监督学习(unsupervised learning)。
对于立体匹配(stereo matching),或者双目深度估计,像LiDAR这样的设备是极其笨重且昂贵的,它所能收集的只是稀疏的深度信息,而我们需要的是密集的深度图(dense depth map);而基于结构光的设备往往只能在室内场景下进行深度信息标注,在室外场景下难以做到较高的标注质量。因此,自监督学习在立体匹配中得到越来越多的关注。本文主要梳理了近年来自监督学习在立体匹配中的应用方法,希望和大家一起探讨学习。
Stereo Matching
立体匹配也称作视差估计(disparity estimation),或者双目深度估计。其输入是一对在同一时刻捕捉到的,经过极线校正的左右图像 l l l_l ll 和 l r l_r lr 。而它的输出是参考图像(一般以左图作为参考图像)中每个像素所对应的视差值所构成的视差图 d d d。视差定义为三维场景中某一点在左右图像中对应点位置的像素级差距。当给定摄像机的基线距离 b b b 和焦距 f f f 之后,我们就可以从视差图中自动计算出深度 d ~ \tilde{d} d~, d ~ = b f / d \tilde{d} =bf/d d~=bf/d.
立体匹配算法分为四个步骤:
- 匹配代价计算(matching cost computation);
- 代价聚合(cost aggregation);
- 视差计算(disparity computation);
- 视差精修(disparity refinement)
传统的视差估计算法主要分为两类:
- 局部算法:主要基于滑动窗口来计算局部窗口内的匹配代价;
- 全局算法:通过优化包括局部数据项和平滑项的能量函数来计算立体视图之间的相关性;
传统的视差估计算法对于各种应用场景都具有等价的视差估计能力,不会因为场景变化而产生较大的差异,因此有论文将传统方法估计的视差图作为带有噪声的标签来提升无监督视差估计的性能,本文后面会提到。随着深度学习的发展以及大规模合成数据的推动,CNN将上述四个步骤统一成一个端到端的网络,进一步提升了视差估计的性能。本文主要探讨的是自监督学习在基于卷积神经网络的视差估计算法中的应用情况。
Self-Supervied Learning
在基于卷积神经网络的立体匹配算法中,有监督学习基本上是回归的方法,即采用smooth L1 loss计算预测的视差值和真实视差值之间的误差来监督网络的学习。自监督学习算法则主要从图像自身的特征结构,视差图自身的特点或者借助传统算法来构造噪声标签来推动网络的学习。
Image Reconstruction Loss
和自编码器类似,我们最容易想到的就是通过重建图像来作loss。假设原来的左图(参考图像)为 I i j l I_{ij}^l Iijl (i,j 表示像素点的位置坐标),根据其预测的视差 d d d 以及原有的右图 I i j r I_{ij}^r Iijr, 我们可以通过warping操作得到重构后的左图 I ~ i j l \tilde{I}_{ij}^l I~ijl 。这里的warping操作是根据左图每个像素点对应的视差值,在右图中寻找对应的像素点再差值得到的。在PyTorch中以grid_sample函数来实现,采样器的原理是基于 Spatial Transformer Network(STN) 得到的,对同一行中的两个像素进行双线性采样,是一个可微的过程。设N为像素点的个数,那么最简单的图像重构损失函数定义如下:
L = 1 N ∑ i , j ∥ I i j l − I ~ i j l ∥ L =\frac{1}{N} \sum_{i, j} \left\|I_{i j}^{l}-\tilde{I}_{i j}^{l}\right\| L=N1i,j∑∥∥∥Iijl−I~ijl∥∥∥
通常,经过重构的图像可能具有很大的失真情况,仅仅采用重构图像和原图的比较还不够,我们会引入图像质量评价中的图像相似度指标SSIM来综合的计算重构图像和原始图像在光度上的误差,
L = 1 N ∑ i , j α 1 − SSIM ( I i j l , I ~ i j l ) 2 + ( 1 − α ) ∥ I i j l − I ~ i j l ∥ L=\frac{1}{N} \sum_{i, j} \alpha \frac{1-\operatorname{SSIM}\left(I_{i j}^{l}, \tilde{I}_{i j}^{l}\right)}{2}+(1-\alpha)\left\|I_{i j}^{l}-\tilde{I}_{i j}^{l}\right\| L=N1i,j∑α21−SSIM(Iijl,I~ijl)+(1−α)∥∥∥Iijl−I~ijl∥∥∥
这里 α \alpha α 是基本重构误差和相似度误差的权重。一般采取单尺度的SSIM以及简化的3×3滤波, α \alpha α一般取0.85,相似度误差占据更大的比重。
Disparity Smoothness Loss
由于我们需要密集的视差图,为了使得视差在局部上保持平滑,我们可以对视差梯度 ∂ d \partial d ∂d 进行L1惩罚。由于深度不连续性通常出现在图像的梯度上,因此图像的梯度 ∂ I \partial I ∂I 也被考虑进来,
L = 1 N ∑ i , j ∣ ∂ x d i j l ∣ e − ∥ ∂ x I i j l ∥ + ∣ ∂ y d i j l ∣ e − ∥ ∂ y I i j l ∥ L=\frac{1}{N} \sum_{i, j}\left|\partial_{x} d_{i j}^{l}\right| e^{-\left\|\partial_{x} I_{i j}^{l}\right\|}+\left|\partial_{y} d_{i j}^{l}\right| e^{-\left\|\partial_{y} I_{i j}^{l}\right\|} L=N1i,j∑∣∣∂xdijl∣∣e−∥∂xIijl∥+∣∣∂ydijl∣∣e−∥∂yIijl∥
left-Right Disparity Consistency Loss
以上两种损失函数是自监督学习中最基本,最常用的损失函数。下面这篇论文提出了左右一致性损失,虽然是基于单目图像的,但是也可以用在双目图像视差估计上。
- 论文标题:Unsupervised Monocular Depth Estimation with Left-Right Consistency
- 论文来源:CVPR 2017 Oral
- 论文地址:https://arxiv.org/abs/1609.03677v3
- 开源代码:https://github.com/mrharicot/monodepth
论文提出的框架如下:
和原有方法不同,输入是左图(双目是左右图),输出不仅是以左图为参考图像的视差图 d l d^l dl, 还有以右图为参考图像的视差图 d r d_r dr。除了应用上述两种损失函数外,还提出了一种左右视差一致性的损失。我们可以将以右图为参考图像的 d r d^r dr 作为warping操作的输入图像,再以左图为参考图像的 d l d^l dl 作为输入的视差图,经过warping操作就会得到 d l d^l dl 的重构视差图。注意,这里得到的是重构的视差图,而非重构的左图。因此,左右视差一致性损失可以写作:
L = 1 N ∑ i , j ∣ d i j l − d i j + d i j l r ∣ L=\frac{1}{N} \sum_{i, j}\left|d_{i j}^{l}-d_{i j+d_{i j}^{l}}^{r}\right| L=N1i,j∑∣∣∣dijl−dij+dijlr∣∣∣
这里N是像素的个数, d i j + d i j l r d_{i j+d_{i j}^{l}}^{r} dij+dijlr 就是重构出来的 d ~ l \tilde{d}^l d~l。
这篇论文中由于预测了两种不同的视差(以左图为参考图像的视差和以右图为参考图像的视差),因此上面提到的三种损失都可以有镜像损失。比如,以原始左图 I l I^l Il,以及以右图为参考图像的视差图 d r d^r dr 作为warping操作的输入,那么得到就是重构出来的右图 I ~ r \tilde{I}^r I~r。
Weighted Local Contrast Normalization
下面这篇论文通过分析重构误差的缺点,提出了一种新的加权局部对比度归一化操作,从而优化了重构误差损失函数。
- 论文标题:ActiveStereoNet: End-to-End Self-Supervised Learning for Active Stereo Systems
- 论文来源:ECCV 2018 Oral
- 论文地址:https://arxiv.org/abs/1807.06009v1
- 复现代码:https://github.com/meteorshowers/StereoNet-ActiveStereoNet
论文提出了一个针对主动视觉的端到端的深度学习方法,我们主要来看其对于重构误差的分析和改进。作者认为光度重构误差具有以下两点不足:
- 在视觉设备感知外部环境时,接收到的信号强度与距离的平方成反比,这导致光度对距离具有明显的依赖。
- 明亮的像素点往往比暗的像素点更容易产生较大的残差。
基于以上两个观察,深度网络在训练时倾向于在容易学习的地方学习(比如,明亮的区域),然后对其他区域进行平滑处理(比如,较暗的区域)。因此,对于较暗的像素点,它需要更准确的深度信息来监督才能学得比较好。但是在自监督学习中,我们缺少的正是这种准确的深度信息(真实的视差标签),这样就会导致较暗的区域学得很差。并且当前景和背景差异较大时,这种损失会在被遮挡的区域产生更大的误差,导致网络无法再继续学习下去。
论文提出的加权局部对比度归一化(WLCN)就是用来移除亮度差异与视差的相关性。具体来说,对每一个像素点,计算以其为中心的9*9区域内的所有像素点的局部均值 μ \mu μ 和标准差 σ \sigma σ,这些局部的统计量用来归一化当前的像素点,
I L C N = I − μ σ + η I_{L C N}=\frac{I-\mu}{\sigma+\eta} ILCN=σ+ηI−μ
其中 η \eta η 是一个小常量。下图展示了LCN归一化后的结果。
由上图可以看出,对于仅使用重构误差(左图),在红色框中较亮的部位对应的重构误差较大。而采用LCN对输入图像归一化处理后(中间图),这些重构误差不会过渡的偏向明亮的区域。这表明LCN不仅消除了光度和视差之间的联系,而且在遮挡区域能够提供较好的残差。
但是另一个问题是,在弱纹理区域局部标准差 σ \sigma σ 可能会趋近于0,从而导致这部分的损失偏大。为了解决这个问题,作者提出使用参考图像在9*9局部区域的标准差 σ i j \sigma_{ij} σij 来作一个重新加权。因此,重构误差可以重写为:
L = ∑ i j ∥ σ i j ( I L C N i j l − I ^ L C N i j l ) ∥ 1 L=\sum_{i j}\left\|\sigma_{i j}\left(I_{L C N i j}^{l}-\hat{I}_{L C N i j}^{l}\right)\right\|_{1} L=ij∑∥∥∥σij(ILCNijl−I^LCNijl)∥∥∥1
从上面图中的右边可以看出,经过重加权之后弱纹理区域的误差也变小了,这是因为这部分对应的权值 σ i j \sigma_{ij} σij 也趋近于0了。
Guided Confidence Loss
除了挖掘图像和视差本身的特性,我们还可以从外部借助一些带有噪声的标签作为监督信息。在本文开头介绍过,传统方法虽然没有基于深度学习的方法性能高,但是对各种场景具有较好的泛化能力。下面这篇论文就是借助传统方法先对图像估计一次视差,再通过置信度的学习来自动的鉴别带有噪声的标签,从而实现在没有标签的条件下的学习。
- 论文标题:Unsupervised Domain Adaptation for Depth Prediction from Images
- 论文来源:PAMI 2019
- 论文地址:https://arxiv.org/abs/1909.03943v1
- 开源代码:https://github.com/CVLAB-Unibo/Unsupervised_Depth_Adaptation
假设由传统算法(比如SGM或者AD-CENSUS)估计的视差值为 D ( p ) D(p) D(p),这里p指的是图像中的像素点。那么以视差图作为输入,几层卷积层构建置信度估计网络,就可以得到该视差图中每一个像素点的置信度,由此构成置信图(confidence map), C ( p ) C(p) C(p)。置信图中每一点的范围在 [0, 1],用来表示生成的视差值的可信程度。如果某点的置信度越高,那么该点处估计的视差值就越准,就越能够作为真实标签来指导深度模型的训练。反之,亦然。
我们可以通过超参数 τ \tau τ 来控制用来指导深度模型训练的参数值。比如 τ = 0.8 \tau = 0.8 τ=0.8 用来表示只有置信度大于0.8的视差值才能成为真正的监督信息。由此看出实际的监督信息是稀疏的,这与KITTI数据标注是一致的,因为它的标注信息也是稀疏的深度值。但是实践证明即使只需要有稀疏的深度信息,已经能够训练出性能很好的模型。
假设由深度模型估计的视差表示为 D ~ ( p ) \tilde{D}(p) D~(p),那么论文提出的引导置信损失可以写作:
L c = 1 ∣ P v ∣ ∑ p ∈ P v E ( p ) L_{c}=\frac{1}{\left|P_{v}\right|} \sum_{p \in \mathcal{P}_{v}} \mathcal{E}(p) Lc=∣Pv∣1p∈Pv∑E(p)
E ( p ) = C ( p ) ⋅ ∣ D ~ ( p ) − D ( p ) ∣ \mathcal{E}(p)=C(p) \cdot|\tilde{D}(p)-D(p)| E(p)=C(p)⋅∣D~(p)−D(p)∣
P v = { p ∈ P : C ( p ) > τ } \mathcal{P}_{v}=\{p \in \mathcal{P}: C(p)>\tau\} Pv={p∈P:C(p)>τ}
这里 P P P 表示的就是由超参数 τ \tau τ 控制的由传统方法估计的稀疏标签,它具有较高的置信度。而深度模型估计的视差和传统方法估计的视差以L1回归的形式监督,包含在loss计算中的像素点由置信度来控制。这种引导置信损失相当于是给深度模型提供了值得信赖的监督信息,但是却是在没有真实标签情况下实现的。
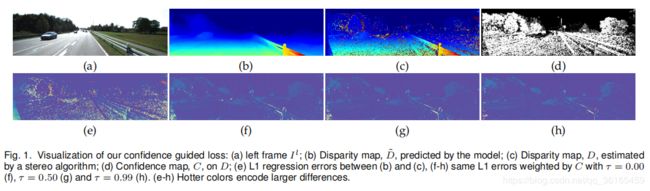
下图给出了不同 τ \tau τ 控制的情况。
从 (e) 到 (h) 我们可以看出, τ \tau τ 越小,监督信息越多,但是相应的噪声也越多; τ \tau τ 越大,虽然噪声较少了,但是准确的监督信息也变少了。因此,超参数 τ \tau τ 也可以纳入到损失函数中一起优化。由于在优化过程中, τ \tau τ 容易收敛到1,作者提出了下面的改进版损失函数:
L c = 1 ∣ P v ∣ ∑ p ∈ P v E ( p ) − log ( 1 − τ ) L_{c}=\frac{1}{\left|P_{v}\right|} \sum_{p \in \mathcal{P}_{v}} \mathcal{E}(p)-\log (1-\tau) Lc=∣Pv∣1p∈Pv∑E(p)−log(1−τ)
新加的项有两个优势,一是将超参数 τ \tau τ 纳入最终的损失函数计算中一起优化,避免了认为调参,可以自动学习出最佳的值;二是以可以约束 τ \tau τ 不收敛到1。
关于超参数 τ \tau τ 的生成,作者提出了两种行之有效的方法:
- 将 τ \tau τ 看做是一个可学习的变量,即上面的描述方式;
- 将 τ \tau τ 看做是一个简单网络的输出,该网络可以采用3个3*3的卷积层,后面接一个全局平均池化得到。
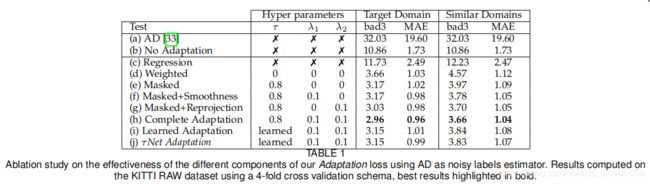
下图是关于超参数 τ \tau τ 的消融实验。
从上图可以看出,无论是将 τ \tau τ 看作学习的变量还是网络的输出,都不如人工交叉验证效果好。
总结
从上面的分析中我们可以归纳出,近年来自监督学习在立体匹配中主要从下面三个方面来考虑:
- 从图像自身的特性出发:如图像重构损失,图像相似度计算,加权局部对比度归一化;
- 从视差图的特点出发:视差平滑损失;
- 从传统方法中借鉴:引导置信损失;
未来的自监督学习我认为可以两方面着手,一是探索如何将图像本身的特性和视差的关系构建起来,因为图像的RGB信息本身和视差信息是没有关系的,图像重构误差本身并不等价于视差回归损失。二是如何获取更加准确的稀疏监督信息,毕竟只需要稀疏的监督信息就能学出很好的视差估计网络,但是前提是监督信息必须准确,也就是少而精。
欢迎关注知乎专栏 双目立体匹配