Python数学模型——线性规划求解（二）

这一篇我们来讨论把某些问题转化为线性规划进行求解，并且举一个实际的例子来操作一下。

可以转化成线性规划问题的情况

1.min |x1|+|x2|+|x3|+……|xn|
s.t. Ax <= b
像这种情况，我们要转化为标准的线性规划问题，可以采用下面的方式：

xi=ui−vi|xi|=ui+viui=(xi+|xi|)/2vi=(|xi|−xi)/2 x i = u i − v i | x i | = u i + v i u i = ( x i + | x i | ) / 2 v i = ( | x i | − x i ) / 2

经过代换以后，可以变为：

min∑i=1n(ui+vi)s.t.:A(u−v)<=bu,v>0 m i n ∑ i = 1 n ( u i + v i ) s . t . : A ( u − v ) <= b u , v > 0

2.min{max{y1,y2……yn}} (y是关于x的线性表达式)
转换方法：

x0=max{y1,y2,y3......yn}s.t.⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪y1−x0<=0y2−x0<=0y3−x0<=0......yn−x0<=0 x 0 = m a x { y 1 , y 2 , y 3 . . . . . . y n } s . t . { y 1 − x 0 <= 0 y 2 − x 0 <= 0 y 3 − x 0 <= 0 . . . . . . y n − x 0 <= 0

例题 投资的收益和风险

市场上有n 种资产s_i （i =1,2,……,n）可以选择，现用数额为M 的相当大的资金,作一个时期的投资。这n 种资产在这一时期内购买s_i 的平均收益率为r_i ，风险损失率为q_i ，投资越分散，总的风险越少，总体风险可用投资的s_i 中最大的一个风险来度量。
购买s_i 时要付交易费，（费率p_i ），当购买额不超过给定值u_i 时，交易费按购买u_i 计算。另外，假定同期银行存款利率是r₀ ，既无交易费又无风险。（ r₀=5% ）已知n = 4时相关数据如表 1。
              
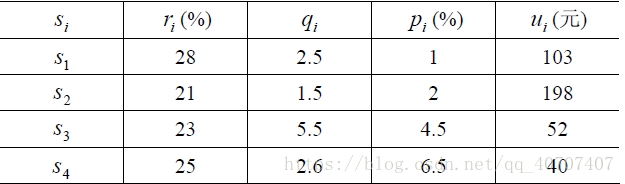
试给该公司设计一种投资组合方案，即用给定资金M ，有选择地购买若干种资产或存银行生息，使净收益尽可能大，使总体风险尽可能小。

1.符号规定：
s_i ：第i 种投资项目，如股票，债券
r_i ，s_i ，q_i ：分别为s_i 的平均收益率，交易费率，风险损失率
u_i ：s_i 的交易定额
r₀ ：同期银行利率
x_i ：投资项目i s 的资金
a ：投资风险度
Q：总体收益

2.基本假设:
a．投资数额M 相当大，为了便于计算，假设M =1；
b． 投资越分散，总的风险越小；
c． 总体风险用投资项目s_i 中最大的一个风险来度量；
d． n 种资产i s 之间是相互独立的；
e．在投资的这一时期内，r_i ,p_i ,q_i ,r₀ 为定值，不受意外因素影响；
f．净收益和总体风险只受r_i ,p_i ,q_i 影响，不受其它因素干扰。

3.模型分析与建立
a.总体风险用所投资s_i 中最大的一个风险衡量，即

max{qixi|i=1,2...,n} m a x { q i x i | i = 1 , 2... , n }

b.购买 s_i 所付交易费是一个分段函数，即

交易费{pixi,xi>uipiui,xi<=ui 交 易 费 { p i x i , x i > u i p i u i , x i <= u i

而题目所给定的定值 u_i （单位：元）相对总投资M 很少， p_i u_i 更小，可以忽略不计，这样购买 s_i 的净收益为 (r_i -p_i)x_i 。
3． 要使净收益尽可能大，总体风险尽可能小，这是一个多目标规划模型：
目标函数为:

{max∑ni=0(ri−pi)ximinmax{qixi} { m a x ∑ i = 0 n ( r i − p i ) x i m i n m a x { q i x i }

约束条件为：

{∑ni=0(1+pi)xi=Mxi>=0,i=0,1,...,n { ∑ i = 0 n ( 1 + p i ) x i = M x i >= 0 , i = 0 , 1 , . . . , n

4.模型简化：
a)固定风险水平，优化收益
给定风险一个界限a，让最大的一个风险q _ix _i/M<=a，找到对应的投资方案。

b)模型二 固定盈利水平，极小化风险

c)投资者在权衡资产风险和预期收益两方面时，希望选择一个令自己满意的投资
组合。因此对风险、收益分别赋予权重s（0 < s ≤1）和(1− s)，s称为投资偏好系数。

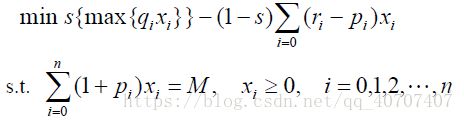
针对三个模型利用Python求解：
模型一的求解：

minf=(0.05,0.27,0.19,0.185,0.185)(x0,x1,x2,x3,x4)Ts.t.⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪x0+1.01x1+1.02x2+1.045x3+1.065x4=10.025x1<=a0.015x1<=a0.055x1<=a0.026x1<=axi>=0(i=0,1,...,4) m i n f = ( 0.05 , 0.27 , 0.19 , 0.185 , 0.185 ) ( x 0 , x 1 , x 2 , x 3 , x 4 ) T s . t . { x 0 + 1.01 x 1 + 1.02 x 2 + 1.045 x 3 + 1.065 x 4 = 1 0.025 x 1 <= a 0.015 x 1 <= a 0.055 x 1 <= a 0.026 x 1 <= a x i >= 0 ( i = 0 , 1 , . . . , 4 )

求解过程：设置a初始值为0，以步长为0.001迭代

a = 0
while a<0.05:
    c = np.array([0.05,0.27,0.19,0.185,0.185])
    A = np.diag([0,0.025,0.015,0.055,0.026])
    b = a*np.ones((5,1))
    Aeq = np.array([[1,1.01,1.02,1.045,1.065]])
    beq = np.array([1])

    res = optimize.linprog(-c,A,b,Aeq,beq)
    x = res.x
    Q = -res.fun
    plt.plot(a,Q,'*')
    a = a+0.001
plt.xlabel('a')
plt.ylabel('Q')
plt.show()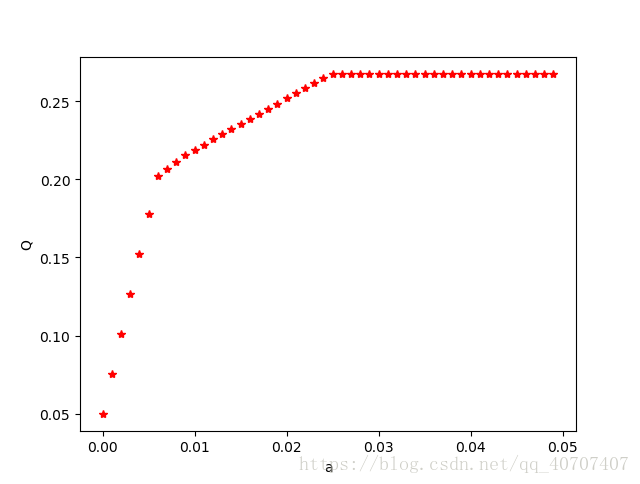

可以看到风险在0.006之后收益增长缓慢，所有我们认为在0.006处兼顾风险，取得最大收益。

模型二的求解：

令x0=max{0.025x1,0.015x2,0.055x3,0.026x4}minz=x0s.t.⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪0.025x1−x0<=00.015x2−x0<00.055x3−x0<=00.026x4−x0<=00.27x1+0.19x2+0.185x3+0.185x4+0.05x5>=k1.01x1+1.02x2+1.045x3+1.065x4+x5=1 令 x 0 = m a x { 0.025 x 1 , 0.015 x 2 , 0.055 x 3 , 0.026 x 4 } m i n z = x 0 s . t . { 0.025 x 1 − x 0 <= 0 0.015 x 2 − x 0 < 0 0.055 x 3 − x 0 <= 0 0.026 x 4 − x 0 <= 0 0.27 x 1 + 0.19 x 2 + 0.185 x 3 + 0.185 x 4 + 0.05 x 5 >= k 1.01 x 1 + 1.02 x 2 + 1.045 x 3 + 1.065 x 4 + x 5 = 1

求解过程：将k赋值为0.05，以0.01步长迭代

k = 0.05
while k<0.27:
    c = np.array([1,0,0,0,0,0])
    A = np.array([[-1,1,0,0,0,0],[-1,0,1,0,0,0],[-1,0,0,1,0,0],[-1,0,0,0,1,0],[0,-0.27,-0.19,-0.185,-0.185,-0.05]])
    b = np.array([0,0,0,0,-k])
    Aeq = np.array([[0,1.01,1.02,1.045,1.065,1]])
    beq = np.array([1])
    res = optimize.linprog(c,A,b,Aeq,beq)
    a = res.fun
    k = k+0.01
    plt.plot(k,a,'*')
plt.xlabel('k')
plt.ylabel('a')
plt.show()

可以看到收益在0.21之后，风险增长率较大，所以为了规避风险，将受益订到0.21。

模型三的求解：

mins∗{max{qi∗xi}}−(1−s)∑i=0(ri−qi)xix0=max{qi∗xi}min{s∗x0−(1−s)∗∑i=0(ri−qi)∗xi}最终得到线性规划问题：mins∗x0−(1−s)∗(0.27x1+0.19x2+0.185x3+0.185x4+0.05x5)s.t.⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪0.025x1−x0<=00.015x2−x0<=00.055x3−x0<=00.026x4−x0<=01.01x1+1.02x2+1.045x3+1.065x4+x5=1 m i n s ∗ { m a x { q i ∗ x i } } − ( 1 − s ) ∑ i = 0 ( r i − q i ) x i x 0 = m a x { q i ∗ x i } m i n { s ∗ x 0 − ( 1 − s ) ∗ ∑ i = 0 ( r i − q i ) ∗ x i } 最 终 得 到 线 性 规 划 问 题 ： m i n s ∗ x 0 − ( 1 − s ) ∗ ( 0.27 x 1 + 0.19 x 2 + 0.185 x 3 + 0.185 x 4 + 0.05 x 5 ) s . t . { 0.025 x 1 − x 0 <= 0 0.015 x 2 − x 0 <= 0 0.055 x 3 − x 0 <= 0 0.026 x 4 − x 0 <= 0 1.01 x 1 + 1.02 x 2 + 1.045 x 3 + 1.065 x 4 + x 5 = 1

求解过程：将s初值设为0，以0.05为步长循环搜索

s = 0
while s<=1:
    c = np.array([s,(s-1)*0.27,(s-1)*0.19,(s-1)*0.185,(s-1)*0.185,(s-1)*0.05])
    A = np.array([[-1,1,0,0,0,0],[-1,0,1,0,0,0],[-1,0,0,1,0,0],[-1,0,0,0,1,0]])
    b = np.array([0, 0, 0, 0])
    Aeq = np.array([[0, 1.01, 1.02, 1.045, 1.065, 1]])
    beq = np.array([1])
    res = optimize.linprog(c,A,b,Aeq,beq)
    fun = res.fun
    s = s + 0.05
    plt.plot(s,fun,'*')
    print(res)
plt.xlabel('s')
plt.ylabel('fun')
plt.show()

通过图像可知，当偏好系数为0.2左右时，符合偏好比例，func绝对值较大，即低风险高收益。

通过上面这个例题，我们探讨了线性规划问题的三种典型情况，希望能给读者带来帮助，如果有意见或者问题欢迎私聊，我们共同解决。