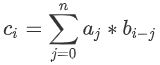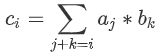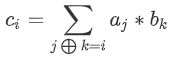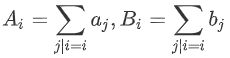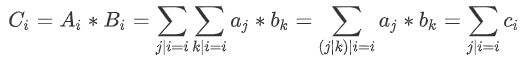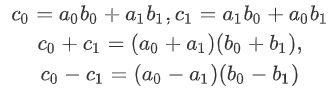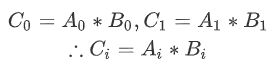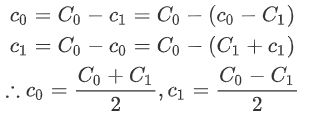专题·快速沃尔什变换（FWT）【including FWT，洛谷P4717【模板】快速沃尔什变换
初见安~这里是樱狸：）
快速沃尔什变换——FWT
FWT是用来快速求解下标位运算关系的卷积的。比如有FFT是求这个：
即
那么FWT求的就是这个：
其中
表示或、与和异或三种运算中的一个【听说还有同或。可惜我不会。
现在我们挨个来推怎么做。【含有FFT的思想，但是不会也问题不大】
1、或（|）
要j和k或起来为i，说明j和k一定都是i的子集。我们设：
所以求出A、B数组，相乘得到C数组，再逆变换回去就可以得到所求的c数组了。这个正逆变幻的过程就是FWT。
现在我们来看如何变换。
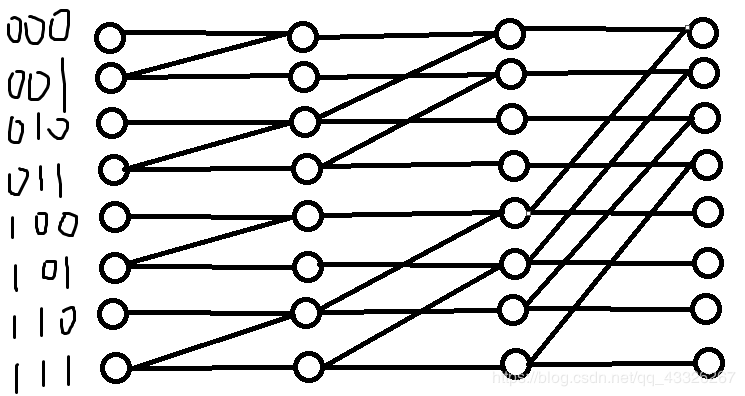
比如A_i，我们可以用递推求解。画一个图吧：
每一行表示一个二进制的数，每一列表示一个转移。第一列的连线表示从右往左第一位减一或者不减可以到达的数，第二列表示第二位，以此类推。可以发现从一个点出发，沿着这些线可以不重复遍历到每个子集。我们设
表示第i个点，看第j位。那么就有：
。并且我们发现j这一维是可以去掉的，所以可以直接写成dp[i]。但是问题来了——中i表示的是点，是状态，而j才是阶段【如图，从左往右的阶段】，所以我们枚举的时候j这一层的循环要放在i外面。
结合这个技巧，我们就可以写FWT_OR的正变换代码了：
void OR(ll *a) {
for(int j = 0; j < m; j++) for(int i = 1; i < n; i++) if(i & (1 << j))
a[i] += a[i ^ (1 << j)];
}现在的问题就是逆变换。既然正变换是加上子集那逆变换减去就好了。【什
再换一种方式来理解吧。因为我们枚举的是每一位，那么我们现在就考虑某一位【为0或1】。最简单的情况，这一位就是第一位。
所以枚举子集，直接减去就好了。
所以OR的代码就是这个样子的：
void OR(ll *a, int op) {
for(int j = 0; j < m; j++) for(int i = 1; i < n; i++) if(i & (1 << j))
a[i] = a[i] + op * a[i ^ (1 << j)];
}2、与（&）
同理，要与起来为i，那么j和k就是i的超集。【换言之i是j和k的子集】
我们刚刚那个图是该位从1连向0，现在就从0连向1【自己动笔画吧我真的懒了】。正反变换都跟或是同理的，直接上代码吧。
void AND(ll *a, int op) {
for(int j = 0; j < m; j++) for(int i = 1; i < n; i++) if(i & (1 << j))
a[i ^ (1 << j)] = a[i ^ (1 << j)] + op * a[i]；
}3、异或（^）
异或就跟与和或不太一样了，要难理解一点。我们还是用代数法推，这次正逆变换一起。
首先同理可得如下等式：
那么我们大胆假设：
带回就有：
至此，正变换搞完了。逆变换我们把假设的内容反过去套：
也就是说，逆变换就相当于正变换过后再除以二就可以了。
代码：
void XOR(ll *a, int op) {
for(int j = 0; j < m; j++) for(int i = 1; i < n; i++) if(i & (1 << j)) {
ll x = a[i ^ (1 << j)], y = a[i];
a[i ^ (1 << j)] = x + y, a[i] = x - y;
if(op == -1) a[i ^ (1 << j)] = a[i ^ (1 << j)] / 2, a[i] = a[i] / 2;
}
}
怎么样是不是还挺简单的：）
好了来看个例题吧：洛谷P4717 FWT板子题
这个题要取模 你取就行了呗。基本就是上文的操作，代码就不解释了。
#include
#include
#include
#include
#include
#include
#define maxn 1 << 20
using namespace std;
typedef long long ll;
const int mod = 998244353;
int read() {
int x = 0, f = 1, ch = getchar();
while(!isdigit(ch)) {if(ch == '-') f = -1; ch = getchar();}
while(isdigit(ch)) x = (x << 1) + (x << 3) + ch - '0', ch = getchar();
return x * f;
}
int n, m;
ll a[maxn], b[maxn], A[maxn], B[maxn], C[maxn], inv = 499122177;
void init() {memcpy(A, a, sizeof A); memcpy(B, b, sizeof B);}
void get() {for(int i = 0; i < n; i++) C[i] = A[i] * B[i] % mod;}
void out() {for(int i = 0; i < n; i++) printf("%lld ", C[i]); puts("");}
void OR(ll *a, int op) {
for(int j = 0; j < m; j++) for(int i = 1; i < n; i++) if(i & (1 << j))
a[i] = (a[i] + op * a[i ^ (1 << j)] + mod) % mod;
}
void AND(ll *a, int op) {
for(int j = 0; j < m; j++) for(int i = 1; i < n; i++) if(i & (1 << j))
a[i ^ (1 << j)] = (a[i ^ (1 << j)] + op * a[i] + mod) % mod;
}
void XOR(ll *a, int op) {
for(int j = 0; j < m; j++) for(int i = 1; i < n; i++) if(i & (1 << j)) {
ll x = a[i ^ (1 << j)], y = a[i];
a[i ^ (1 << j)] = (x + y) % mod, a[i] = (x - y + mod) % mod;
if(op == -1) a[i ^ (1 << j)] = a[i ^ (1 << j)] * inv % mod, a[i] = a[i] * inv % mod;
}
}
signed main() {
m = read(); n = 1 << m;
for(int i = 0; i < n; i++) a[i] = read() % mod;
for(int i = 0; i < n; i++) b[i] = read() % mod;
init(); OR(A, 1), OR(B, 1); get(), OR(C, -1), out();
init(); AND(A, 1), AND(B, 1); get(), AND(C, -1), out();
init(); XOR(A, 1), XOR(B, 1); get(), XOR(C, -1), out();
return 0;
} 迎评：）
——End——