专题·最短路【including Dijkstra， SPFA，Floyd，传递闭包，二维最短路，分层图最短路，最短路计数……

初见安~终于想起来要整理去年学的最短路了QwQ

首先最短路的定义是很简单的——图上两点之间最短的距离就是最短路。

下面开始介绍三种求法——

一、单源最短路

所谓单源最短路，就是固定出发点【源头】，求其到达其他所有点的距离。

1.Dijkstra（迪杰斯特拉） 算法

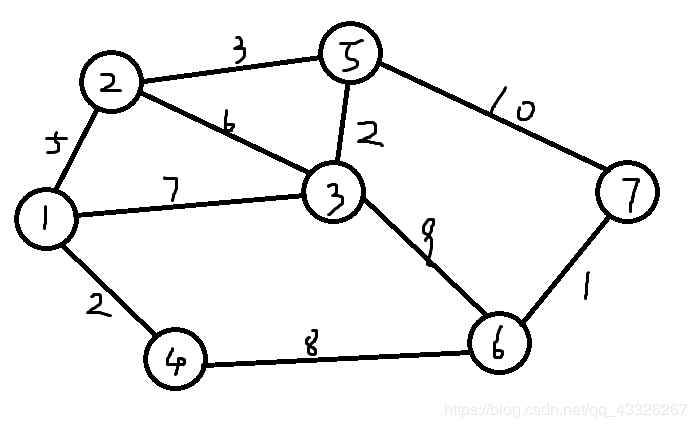
先放一个样例图：【有不符合几何定义的三角形是很正常的！！！】

图中，我们假设点1为出发点，求出1到所有其他点的距离。

一开始dis数组我们要全部赋值为极大值，并dis[ 1 ] = 0。

从1开始，我们先走过和1连出去的所有边，更新节点2、3、4。而后又可以从这三个节点选择一个继续搜下去。因为我们求的是最短路，所以我们选一个目前dis最小的节点进行扩展。假设当前节点为u，扩展到的节点为v，两点之间边权为w，只要在扩展图中发现存在就可以直接更新dis[ v ]的值了。也就是说每次都找到一个点来更新其他所有点的dis，这样下来时间复杂度为。核心代码如下：【这是最原始和暴力的写法，邻接矩阵存图】

void dij()
{
	memset(dis, 0x3f, sizeof dis);
	memset(vis, 0, sizeof vis);
	dis[1] = 0;
	for(int i = 1; i < n; i++)
	{
		int x = 0;//当前dis最小的点
		for(int j = 1; j <= n; j++)//vis的作用是保证每个点全局只被用来更新别的点一次。 
			if(!vis[j] && (x == 0 || dis[j] < dis[x])) x = j; 
			
		vis[x] = 1;
		for(int j = 1; j <= n; j++)//当然，这里用邻接表的话也可以省一些时间和空间
			dis[j] = min(dis[j], dis[x] + g[x][j]); //g是邻接矩阵 
	}
}//入口：直接调用即可。

但是看起来代码很简短，不论是时间还是空间，复杂度都很高。所以就有了dijkstra的堆优化——不用每次O(n)地找最小的dis节点，而是用一个堆来维护，这样复杂度就可以降到。

下面是堆优化的核心代码：【优化后用邻接表了】

priority_queue > q;//优先队列本为大根堆，这里的pair前者用于排序
//priority_queue, vector >, greater > > q;
//如果不想写大根堆+相反数维护的话，直接这样写小根堆也可以。
void dij()
{
    memset(dis, 0x3f, sizeof dis);
    dis[1]=0;
    q.push(make_pair(0,1));
    while(q.size())
    {
        int u=q.top().second;q.pop();//取出堆顶的点
        if(vis[u]) continue;//如果已经被用来更新过别的点了，就不用了
        vis[u]=1;
        for(int i=head[u];~i;i=e[i].next)//这里用邻接表了，因为没有连边的点矩阵也更新不到
        {
            int v=e[i].v;
            int w=e[i].w;
            if(dis[v]>dis[u]+w)//可以更新
            {
                dis[v]=dis[u]+w;
                q.push(make_pair(-dis[v],v));//dis存相反数是为了在大根堆里得到较小的那一个。
            }
        }
    }
}

所以说白了，dijkstra算法的核心就在于每次用当前dis最小的节点去更新别的节点。

*线段树优化版本

因为优先队列虽然确实是优化了，但是常数还是很大的。其作用也就是返回区间的最小值，并且如果用过了就弹出去。这种裸的RMQ不是可以用线段树维护嘛！！！而且常数远小于优先队列。所以我就着手写了一下——

用线段树维护的话，要开一个ans数组存答案，再开一个线段树支持查询和修改。因为如果返回的dis最小的点已经用过了，我们是不会再拿来用的，所以每次用过一个节点过后要在线段树上将其值赋值为INF，覆盖掉答案，这也是为什么要单独开一个ans存答案。

具体操作可以自己去思考一下，就是码量有点儿大……

#include
#include
#include
#include
#include
#include
#define maxn 100005
#define inf 2147483647
using namespace std;
typedef long long ll;
int read() {
	int x = 0, f = 1, ch = getchar();
	while(!isdigit(ch)) {if(ch == '-') f = -1; ch = getchar();}
	while(isdigit(ch)) x = (x << 1) + (x << 3) + ch - '0', ch = getchar();
	return x * f;
}

int n, m;
struct edge {
	int to, w, nxt;
	edge() {}
	edge(int t, int ww, int nn) {to = t, w = ww, nxt = nn;}
}e[maxn << 1];

int head[maxn], k = 0;
void add(int u, int v, int w) {e[k] = edge(v, w, head[u]); head[u] = k++;}

ll ans[maxn];
struct node {
	ll dis; int x;
	node() {}
	node(ll d, int xx) {dis = d, x = xx;}
}dis[maxn << 2];

//建树初始化，主要是编号也要返回所以要先预处理一下 
void build(int p, int l, int r) {
	if(l == r) {dis[p].x = l; return;}
	int mid = l + r >> 1;
	build(p << 1, l, mid); build(p << 1 | 1, mid + 1, r);
	dis[p].x = dis[p << 1].x;
}

void change(int p, int l, int r, int x, int y) {
	if(l == r) {dis[p].dis = y; return;}
	int mid = l + r >> 1;
	if(x <= mid) change(p << 1, l, mid, x, y);
	else change(p << 1 | 1, mid + 1, r, x, y);//单点修改的板子操作 
	if(dis[p << 1].dis < dis[p << 1 | 1].dis) dis[p] = dis[p << 1];
	else dis[p] = dis[p << 1 | 1];
}

//因为用距离得到最小，但是需要的是编号，所以返回node 
node ask(int p, int l, int r, int ls, int rs) {
	if(ls <= l && r <= rs) {return dis[p];}
	int mid = l + r >> 1; node ans = node(inf, 0), tmp;
	if(ls <= mid) ans = ask(p << 1, l, mid, ls, rs);
	if(rs > mid) {
		node tmp = ask(p << 1 | 1, mid + 1, r, ls, rs);
		if(ans.dis > tmp.dis) ans = tmp;
	}
	return ans;
}

int S;
void dij() {
	for(int k = 1; k < n; k++) {//n-1次够用的。虽然我也不知道为什么最后n次跑的比n-1次还要快…… 
		register int u = ask(1, 1, n, 1, n).x;
		for(int i = head[u]; ~i; i = e[i].nxt) {
			register int v = e[i].to;
			if(ans[u] + e[i].w < ans[v]) {//最短路更新 
				ans[v] = ans[u] + e[i].w, change(1, 1, n, v, ans[v]);//单点修改 
			}
		}
		change(1, 1, n, u, inf);//取出来过后要赋值INF，以免再次取用 
	}
}

signed main() {
	memset(head, -1, sizeof head);
	n = read(), m = read(), S = read();
	for(int u, v, w, i = 1; i <= m; i++) u = read(), v = read(), w = read(), add(u, v, w);
	
	//初始化 
	for(int i = 1; i <= (n << 2); i++) dis[i].dis = inf;
	for(int i = 1; i <= n; i++) ans[i] = inf;
	
	//线段树初始化，dis是线段树，ans是答案 
	build(1, 1, n);
	change(1, 1, n, S, 0); ans[S] = 0;
	dij();
	
	for(int i = 1; i <= n; i++) printf("%lld ", ans[i]);
	return 0;
}

来对比一下速度：

 

明显要快很多的~

2、SPFA

*这个算法是对Bellman-ford算法【就不介绍了】的一个队列优化。可用于求单源最短路。

如果说dijkstra是步步回头找最小，那么SPFA就是一点一圈扩散去。每到一个点，就直接枚举和它相连的所有边和点，如果走这条路可以更近，那么就更新那个点的dis。如果那个点不在即将更新的队列里，那就放进去。也就是十分类似于BFS的一种做法。在这种做法下，每个点可能被放进队列多次，但是都是带着更新前面的点的dis 的可能进去的。这样不断更新，直到已经没有哪个点更新别的点，就说明已经得到最短路了。

如果没有明白，那么可以先看看代码——

void spfa()
{
	memset(dis, 0x3f, sizeof dis);
	dis[1] = 0; vis[1] = 1;//vis记录是否在队列里 
	queue q;
	q.push(1);
	register int u, v;
	while(q.size())
	{
		u = q.front(); q.pop(); vis[u] = 0;
		for(int i = head[u]; ~i; i = e[i].nxt)//向外发散 
		{
			v = e[i].to;
			if(dis[u] + e[i].w < dis[v])
			{
				dis[v] = dis[u] + e[i].w;
				if(!vis[v]) q.push(v), vis[v] = 1; //不在队列中，那就放进去更新别的点 
			}
		}
	}
}

两种算法的核心都是找到另一条路来更新当前的最短路，但是实现方法不大一样。某种程度上说，dijkstra因为即使是堆优化，优先队列的常数也是很大的，而SPFA在稀疏图下步步发散就可以跑得很快，所以有时SPFA可以比Dijkstra快很多，算法的复杂度可以达到O(km)【k为常数】的级别。但是如果是稠密图的话，SPFA也可以退化到O(nm)。所以两种算法也是各有优势，才能一起存活下来。当然，SPFA也是可以用优先队列 优化队列的，实现方法最后就和Dijkstra差不多了。

单源最短路的板子题很多，像热浪之类的都可以拿来练练手。

SPFA还有一个作用——差分约束【传送门建设中】。

二、多源最短路

前面介绍了一个出发点到任意一点的算法，那么求任意两地之间的呢？

当然可以for1~n，不断调用单源最短路的函数。

不过有一个更简单的算法——

Floyd

这个算法可以在的时间和的空间内求出任意两点之间的最短路。其原理也是十分的简单粗暴——直接看代码都能明白。

【读入用的邻接矩阵，初始化极大值，直接读入边与边的关系存入dis】

void Floyd()
{
	for(int k = 1; k <= n; k++)//注意，一定要先枚举中转节点保证三角形的情况
		for(int i = 1; i <= n; i++)
			for(int j = 1; j <= n; j++)
				dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);
} 

顺带解释一下为什么k的这层循环要放在最外面。因为如你所见，Floyd的本质其实是dp。dp需要的是什么？阶段和状态。如果说到了点（i，j）这就是状态的话，那么阶段呢？就是K了。因为Floyd的原始写法其实是：

，其中Ｋ表示的是用第1~k号以内的点，得到的i到j的最短路。所以k其实也是表示的阶段，而阶段的枚举是一定要放在最外层的。

看起来n三方的算法很不靠谱啊。事实上更多的时候我们还是会选择floyd，因为好写。而且只要保证不会爆TLE就是一定可以直接用的。当然，选择用哪种算法取决于具体的题目。比如涉及到最短路径树的问题，多源时用for调用SPFA是最优的。

*传递闭包

Floyd算法不仅可以实值求最短路，也可以维护关系——比如，当前值能不能通过已经更新出来了的东西 更新出来。具有传递性。

同理，建立邻接矩阵，d[ i ] [ j ] = 1表示 i 和 j 有关系，为0表示没有关系。

可以用Floyd求出所有的关系：

void Floyd()
{
	for(int k = 1; k <= n; k++)//注意，一定要先枚举中转节点保证三角形的情况
		for(int i = 1; i <= n; i++)
			for(int j = 1; j <= n; j++)
				dis[i][j] |= dis[i][k] & dis[k][j];
} 

看起来可能确实没什么用，但是当你在求某个问题过后，你需要得到在当前环境下某两个点是否联通，就可以直接Floyd传递闭包走一波，然后看dis[ i ] [ j ] & dis[ j ] [ i ]是否为1即可。

三、K短路

直接传送：专题·k短路。

四、二维最短路

直接传送：Poj P1724 ROADS

五、最短路分层图

毕竟看例题比较直接所以继续传送QwQ：洛谷P4568 [JLOI2011]飞行路线

六、最短路径树

不解释了……专题·最短路径树

顺便提醒：最短路径树可以求的是最短路径树的数量，并不等于最短路的数量，所以一定要区分开。

七、最短路计数

良心一点……开始讲解……

最短路计数问题，暴力一点我们可以直接在priority_queue求出最短路后继续等待最短路的出现，直到出现的到目标节点的距离大于我们先前计数的最短路距离。但是会被瞬间T掉。所以我们不妨想想在过程中计数——如果有从u->v的边，连过去后和目前得出的最短路长度相同，那么到达v的路径就多了一些，相当于是；而如果是发现路径更短了，就要覆盖掉。那么直接覆盖好了：。最后输出终点的最短路计数即可。

有没有感觉其实很简单！！！！！有一个例题【这次是题目链接，没有写题解……QAQ】洛谷P1608 路径统计。这个题很恶毒的地方就在于，其数据重边的情况很严重。因为是计数问题，所以一旦重边，邻接表是无法处理多余的计数的。遇到这种问题——只要n的范围允许就开邻接矩阵吧，那是最保险的。

*八、求两对点的最短路的最大重合路径长度

有向图：洛谷P3106 GPS的决斗Dueling GPS's

无向图：【较难】洛谷P2149 Elaxia的路线

以上就是关于最短路的全部问题啦~~~【好水啊全是传送门QAQ】

迎评：）
——End——