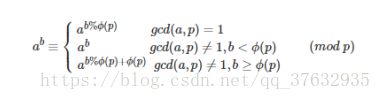2019ICPC南京站B题super_log

题目链接：https://nanti.jisuanke.com/t/41299

In Complexity theory, some functions are nearly O(1)O(1)O(1), but it is greater then O(1)O(1)O(1). For example, the complexity of a typical disjoint set is O(nα(n))O(nα(n))O(nα(n)). Here α(n)α(n)α(n) is Inverse Ackermann Function, which growth speed is very slow. So in practical application, we often assume α(n)≤4α(n) \le 4α(n)≤4.

However O(α(n))O(α(n))O(α(n)) is greater than O(1)O(1)O(1), that means if nnn is large enough, α(n)α(n)α(n) can greater than any constant value.

Now your task is let another slowly function log∗log*log∗ xxx reach a constant value bbb. Here log∗log*log∗ is iterated logarithm function, it means “the number of times the logarithm function iteratively applied on xxx before the result is less than logarithm base aaa”.

Formally, consider a iterated logarithm function loga∗log_{a}^* loga∗​

Find the minimum positive integer argument xxx, let loga∗(x)≥blog_{a}^* (x) \ge bloga∗​(x)≥b. The answer may be very large, so just print the result xxx after mod mmm.

Input

The first line of the input is a single integer T(T≤300)T(T\le 300)T(T≤300) indicating the number of test cases.

Each of the following lines contains 333 integers aaa , bbb and mmm.

1≤a≤10000001 \le a \le 10000001≤a≤1000000

0≤b≤10000000 \le b \le 10000000≤b≤1000000

1≤m≤10000001 \le m \le 10000001≤m≤1000000

Note that if a==1, we consider the minimum number x is 1.

Output

For each test case, output xxx mod mmm in a single line.

Hint

In the 4−th4-th4−th query, a=3a=3a=3 and b=2b=2b=2. Then log3∗(27)=1+log3∗(3)=2+log3∗(1)=3+(−1)=2≥blog_{3}^* (27) = 1+ log_{3}^* (3) = 2 + log_{3}^* (1)=3+(-1)=2 \ge blog3∗​(27)=1+log3∗​(3)=2+log3∗​(1)=3+(−1)=2≥b, so the output is 272727 mod 16=1116 = 1116=11.

样例输入复制

5
2 0 3
3 1 2
3 1 100
3 2 16
5 3 233

样例输出复制

1
1
3
11
223

题目理解：

其实就是求a^(a^(a^(a^(a^...)))) ，其中有b个a，求其对mod取余后的结果，cf有一道题和这个类似，很经典的欧拉降幂的做法，可惜当时没做过这个专题，奈何学长强大QAQ！！！，tql，现在补的时候发现好像也不是特别难，而且数据好像就只有三组（？？？）。

需要知道下面的公式

具体做法参考代码实现（搬一下bzoj3884的题解，很类似，求2^(2^(2^(2^(2^...)))) mod p的结果）。

#include
#define ll long long
using namespace std;
map euler;
ll a,b,mod;
int phi(int n)
{
    int now=n;
    int ret=n;
    if(euler.count(now)) return euler[now];
    for(int i=2;i<=sqrt(n);i++)
    {
        if(n%i==0)
        {
            ret=ret/i*(i-1);
            while(n%i==0)
                n/=i;
        }
    }
    if(n>1)
        ret=ret/n*(n-1);
    euler[now]=ret;
    return ret;
}
ll MOD(ll n,int mod)
{
    return n>=1);
    return ret;
}
ll solve(int l,int r,int mod)
{
    if(l==r||mod==1) return MOD(a,mod);
    return quick_mod(a,solve(l+1,r,phi(mod)),mod);
}
int main()
{
    int T;
    scanf("%d",&T);
    while(T--){
    	scanf("%lld%lld%lld",&a,&b,&mod);
    	if(a==1||b==0){
    		printf("%d\n",1%mod);
    		continue;
		}
		if(b==1){
			printf("%d\n",a%mod);
			continue;
		}
        ll ans=solve(1,b,mod)%mod;
        printf("%lld\n",ans);
	}
    
}