论文阅读笔记2——Evading Defenses to Transferable Adversarial Examples by Translation-Invariant Attacks

论文标题：Evading Defenses to Transferable Adversarial Examples by Translation-Invariant Attacks

论文链接：https://arxiv.org/abs/1904.02884

• 关于对抗攻击：

白盒攻击（white-box attacks）：在已经获取机器学习模型内部的所有信息和参数上进行攻击。已知给定模型的梯度信息生成对抗样本，如fast gradient sign method（FGSM），basic iterative method，Carlini & Wagner’s method。

黑盒攻击（black-box attacks）：在神经网络结构为黑箱时，仅通过模型的输入和输出，生成对抗样本。

跨模型可转移性（cross-model transferability）：对一个模型制作的对抗样本在很大概率下会欺骗其他模型。可转移性使得黑盒攻击（black-box attacks）能够应用于实际，并引发严重的安全问题（自动驾驶、医疗）。

生成的对抗样本与判别区域或白盒模型给定的输入点的梯度高度相关，而其他模型依赖于不同的区域做预测，这使得转移到其他防御模型很困难。

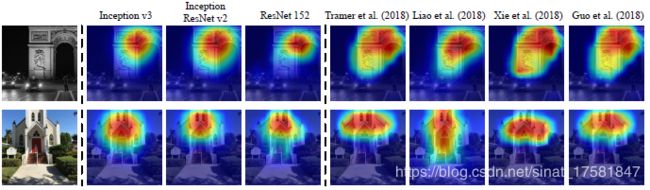
普通模型有相似的attention maps，防御模型会产生不同的attention maps。防御模型的辨别目标类别的识别区域（discriminative regions）与其他正常训练的模型不同，见图1。当用FGSM、BIM等已有模型生成对抗样本，只是对于单一的样本进行优化，因此会与识别区域或白盒模型在被输入数据的攻击点的梯度高度相关。对于另一个有着不同识别区域的黑盒模型，该对抗样本很难保持对抗性。

图1 采用类别激活图（class activation mapping）将三种普通模型以及四种防御模型的attentioin maps 可视化

Fast gradient sign method（FGSM）：如图 1‑1，在输入的基础上沿损失函数的梯度方向加入了一定的噪声，使目标模型产生了误判。FGSM可以生成高转移性的对抗样本，但是对于攻击白盒模型，效率不高。

                                                             图2 FGAM生成对抗样本

Basic Iterative Method (BIM)：FGSM对于梯度更新1次，而BIM更新多次： 

                             

其中，α=ϵ/T，T为迭代次数。BIM比FGSM引起更强大的白盒攻击，但是以较差的可转移性为代价。

Momentum Iterative Fast Gradient Sign Method(MI-FGSM)：在迭代攻击方法中加入动量项（momentum term），提高对抗样本的转移性：

                              

其中gt包含了直到t次迭代的梯度信息。

Diverse Inputs Method：对输入进行随机转换，将转换后的图像送入分类器计算梯度。转换包括随机调整大小和填充给定的分布。该方法可以与基于动量的方法结合来提高转移性。

• 贡献：

为了减轻模型间不同识别区域带来的影响，提出转移不变攻击（translation-invariant attack）方法。对一个包含图像和其转移图像的集合生成对抗样本，希望该对抗样本对于被攻击的白盒模型的识别区域不敏感，比较容易欺骗另一个黑盒模型。要生成这样的样本需要计算集合中所有图像的梯度，这需要很大的计算量。为了提高效率，该文献提出一种通过对未转移的图像做卷积梯度的方法，其中卷积核是预定的。将该方法与任意基于梯度的攻击结合，以同样的计算复杂度得到了大量转移性对抗样本。

• 技术：

对于一般的对抗样本生成问题，目标函数是最大化对抗样本和真实样本对应的标签y间的损失函数J(,y)，所以优化函数为：

                                

为了生成对白盒模型的识别区域不敏感的对抗样本，文献采用的方法是用一系列平移后的图像来优化对抗样本：

                                     

其中，Tij(x)是平移函数（translation operation），将图像x在对应维度平移i、j个像素点，即T，设置i,j∈{-k,…,0,…,k}，k为平移的最大像素值。这样，生成的对抗样本将减弱对被攻击的白盒模型的识别区域的敏感，这能够帮助其转移到其他模型。

对于上述优化算法，需要计算张图像的梯度。CNN是有平移不变性的（translation-invariant property），输入图像中的目标被识别与其位置无关。事实上，CNN不是严格的平移不变的， 所以假设平移不变性是在较小的移动下才能保持。令k<=10，基于以上假设：         

                                     

经过一系列推倒，得：

                     

                   

因此，不需要求得个图像的梯度，而是求未平移图像的梯度，然后对平移的梯度求平均，也等价于对梯度和由权值wij组成的核做卷积。W是大小为(2k+1)×(2k+1)的核矩阵，。对于核矩阵的选择，原则是图像平移越大，权值要越小，以使得对抗扰动能够欺骗模型，文献给出了三种选取方法：

以上求梯度的方法可以与任意基于梯度的攻击方法结合：

Translation-invariant fast gradient sign method（TI-FGSM）更新规则为：

Translation-invariant basic iterative method（TI-BIM）更新规则为：