【机器学习】笔记之聚类Cluster—— 层次聚类 Hierarchical clustering

本文转载翻译自斯坦福大学出版的 Introduction to Information Retrieval

什么是层次聚类Hierarchical clustering?

平面聚类是高效且概念上简单的，但它有许多缺点。 算法返回平坦的非结构化簇集合，需要预先指定的簇数目作为输入并且这个数目是不确定的。 分层聚类（或分层聚类）输出层次结构，这种结构比平面聚类返回的非结构化聚类集更具信息性。 分层聚类不需要我们预先指定聚类的数量，并且在IR(Information Retrieval)中使用的大多数分层算法是确定性的。 分层聚类的这些优点以降低效率为代价。 与K-means和EM的线性复杂度相比，最常见的层次聚类算法具有至少二次的文档数量的复杂性。

平面和层次聚类在信息检索中的应用差异很小。 特别是，分层聚类适用于该文章中Table1中所示的任何应用程序。 实际上，我们为collection clustering提供的示例是分层的。 一般来说，当考虑聚类效率时，我们选择平面聚类，当平面聚类的潜在问题（不够结构化，预定数量的聚类，非确定性）成为关注点时，我们选择层次聚类。 此外，许多研究人员认为，层次聚类比平面聚类产生更好的聚类。 但是，在这个问题上没有达成共识（见第17.9节中的参考文献）。

我们首先介绍了凝聚层次聚类（第17.1节），并在第17.2-17.4节介绍了四种不同的凝聚算法，它们采用的不同的相似性量度：single-link, complete-link, group-average, and centroid similarity。 然后，我们将在第17.5节讨论层次聚类的最优性条件。 第17.6节介绍了自上而下（divisive）的层次聚类。 第17.7节着眼于自动标记聚类，这是人类与聚类输出交互时必须解决的问题。 我们在第17.8节讨论实现问题。 第17.9节提供了进一步阅读的指示，包括对软分层聚类的引用，我们在本书中没有涉及。

凝聚分层聚类(Hierarchical agglomerative clustering):

分层聚类算法可以是自上而下的，也可以是自下而上的。 自下而上算法在开始时将每个文档视为单个簇，然后连续地合并（或聚合）簇对，直到所有簇已合并到包含所有文档的单个簇中。 因此，自下而上的层次聚类称为凝聚分层聚类或HAC。在介绍HAC中使用的特定相似性度量之前，我们首先介绍一种以图形方式描述层次聚类的方法，讨论HAC的一些关键属性，并提出一种计算HAC的简单算法。

HAC聚类通常可视化为树状图(Dendrogram)，如图1所示。 每个合并由水平线表示。 水平线的y坐标是合并的两个聚类的相似度（cosine similarity: 1为完全相似，0为完全不一样），其中文档被视为单个聚类。 我们将这种相似性称为合并簇的组合相似性(combination similarity)。

Figure 1.  A dendrogram of a single-link clustering of 30 documents from Reuters-RCV1. 两个可能的分割：0.4划分成24个簇；0.1划分成12个簇.

通过从底层向上移动到顶层节点，树形图允许我们重建已经合并的簇。 例如，我们看到名为War hero Colin Powell的两个文件首先在Figure 1中合并，并且在最后一次合并中加入了Ag trade组成了一个包含其他29个文件组成的簇。 HAC的一个基本假设是合并操作是单调的。 单调意味着如果是HAC的连续合并的组合相似性，则成立。分层聚类不需要预先指定数量的聚类。 但是，在某些应用程序中，我们需要像平面聚类一样对不相交的簇进行分区。 在这些情况下，需要在某个时刻削减层次结构。 可以使用许多标准来确定切割点：

• 削减预先指定的相似度。 例如，如果我们想要最小组合相似度为0.4的聚类，我们将树形图切割为0.4。 在图1中，以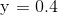切割图表产生了24个聚类（仅将具有高相似性的文档组合在一起），并将其切割为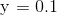，产生12个聚类（一个大型财经新闻聚类和11个较小聚类）。
• 如果两个连续的组合相似性之间的差距最大，那么就在此处切割树。 如此大的差距可以说是“自然的”聚类。 再添加一个簇会显着降低聚类的质量，因此需要在发生这种急剧下降之前进行切割。 This strategy is analogous to looking for the knee in the -means graph in Figure 16.8 (page 16.8 ).
• 应用公式：

其中指的是导致个簇的层次结构的削减，RSS是剩余的平方和(residual sum of squares)，是每个额外簇的惩罚。 可以使用另一种失真度量来代替RSS。

• 与平面聚类一样，我们也可以预先指定聚类的数量并选择产生聚类的切割点。

一个简单的HAC算法如Figure 2所示。 我们首先计算相似度矩阵。然后该算法执行步(e.g.10个样本需要N-1=9次来最终将所有样本cluster到一起)来合并当前最相似的簇。 在每次迭代中，合并两个最相似的簇(比如  和 )，将这个簇与其他簇从新计算相似度并更新到相似度矩阵中的行和列。这样做的目的是利用来表示新合并好的簇。然后将 deactivated，这样做在以后的迭代中，便用来代表包含的簇，而将不再被考虑（已经被聚类）。合并形成的簇以列表的形式存储在中。表示哪些群集仍然可以合并(如前文所说的，若没有被聚类则否则)。 函数计算簇与簇和合并的相似性。 对于某些HAC算法，只是和的函数，例如，这两者中的single-link的值。 

Figure 2. A simple, but inefficient HAC algorithm

 

相似性度量：Single-link and complete-link clustering：

                           

Single-link clustering: 在single-link clustering中，两个聚类的相似性是其最相似成员的相似性。 Single-link合并标准是本地的。 也就是说，我们只关注两个簇彼此最接近的区域， 其他更远的簇的整体结构不予考虑。参考Figure 2(a)。

Complete-link clustering: 在Complete-link中，两个聚类的相似性是它们最不相似的成员的相似性。 这相当于选择合并具有最小直径的簇对。 Complete-link合并标准是非本地的; 簇的整个结构可以影响合并决策。 这导致Complete-link倾向于在长的，散乱的簇上选择具有小直径的紧密簇，但也导致对异常值的敏感性。 远离中心的单个文档可以显着增加候选合并集群的直径，并完全改变最终的集群。参考Figure 2(b)。

Figure 2. The different notions of cluster similarity used by HAC algorithms

                                

Figure 17.2描绘了八个文档的Single-link and Complete-link clustering。 前四个步骤，每个步骤产生一个由两个文档组成的簇，两种方法的结果是相同的。 然后Single-link clustering连接上面的两对，之后是下面的两对，因为在聚类相似性的最大相似性定义上，这两个聚类最接近。 Complete-link clustering连接左两对（然后是右两对），因为根据聚类相似性的最小相似性定义，它们是最接近的对。

                                  

Figure 1是一组文档的Single-link cluster的示例，Figure 3是同一组文件的Complete-link cluster。当切割Figure 3中的最后一个合并时，我们获得两个相似大小的簇。 Figure 1中的树状图没有这样的切割可以为我们提供同样平衡的聚类。 

 

Figure 3. A dendrogram of a complete-link clustering of 30 documents from Reuters-RCV1. 

Single-link and Complete-link clustering都具有图形理论解释。将定义为合并步骤中的两个簇的组合相似度，将定义为已经根据相似度大于的相似度合并好的树（我的理解：将定义为截止到第步所合并形成的树图）。 在完成了次聚类以后，通过Single-link clustering形成的树包含了很多connected components，而通过Complete-link形成的树则包含了很多cliques。

Connected components：A maximal set of connected points such that there is a path connecting each pair.

Clique: A clique is a set of points that are completely linked with each other.

到这为止，我们要清楚：Single-link clustering在每一次聚类时，只要当前即将要合并的两个簇中保证有一个样本样本对的相似度最大即可。而在Complete-link clustering中，即将要合并的两个簇必须要保证所有样本对的相似度都很小（根据两个簇最不相似的样本对相似最大，那么这两个簇中任意的两个样本对的相似度必都大于最不相似样本对相似度）。就好比是一个朋友圈，这个圈子里只要有一个人喜欢你，就把你加进来——Single-link cluster；所有人都喜欢你才能把你加进来——Complete-link clustering。

链式效应在Figure 1中也很明显。 Single-link clustering的最后十一个合并（超过行的那些）添加单个文档或文档对，可看作是链式效应。 Figure 3中的Complete-link clustering避免了这个问题。 当我们在最后一次合并时剪切树形图时，文档被分成两组大小相等的大小。 通常，我们更想得到一个平均的集群而不是链式的集群。

但是，Complete-link clustering会遇到不同的问题。 它过分关注异常值，这些点不适合集群的全局结构。 在Figure 4的示例中，四个文档由于左边缘的异常值而被拆分。 在此示例中，Complete-link clustering未找到最直观的群集结构。