Python-计量经济学案例
python线性回归
- 二元线性回归:
- code:
- output:
- 化为线性的非线性实例:
- code:
- output:
- 虚拟变量(哑变量):
- code:
- output:
- 因变量预测:
- code:
- output:
二元线性回归:
模型假设:
假设中国2013年各地区人均现金消费支出与工资性收入、其他收入之间的关系为:
Y = β 0 =\beta_0 =β0+ β 1 X 1 \beta_1X_1 β1X1+ β 2 X 2 \beta_2X_2 β2X2+ μ \mu μ
通过python的statsmodels库对数据进行回归计算:
code:
import statsmodels.api as sm
import seaborn as sns
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn import model_selection
data = pd.read_excel(r'C:\Users\仁义\Desktop\data.xlsx', sheet_name='Sheet1')
fit = sm.formula.ols(formula='现金消费支出Y ~ 工资性收入X1 + 其他收入X2', data=data).fit()
print(fit.summary())
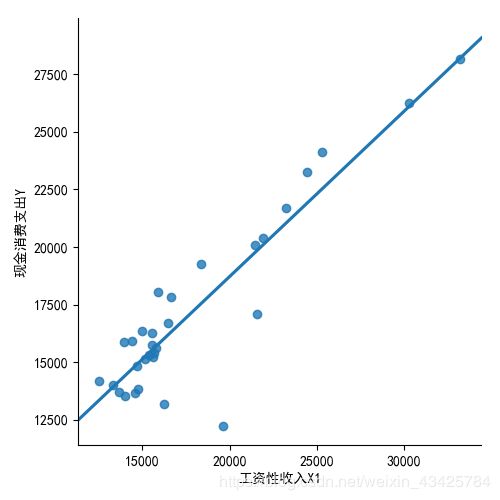
sns.lmplot(x='工资性收入X1', y='现金消费支出Y', data=data, ci=None)
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.show()
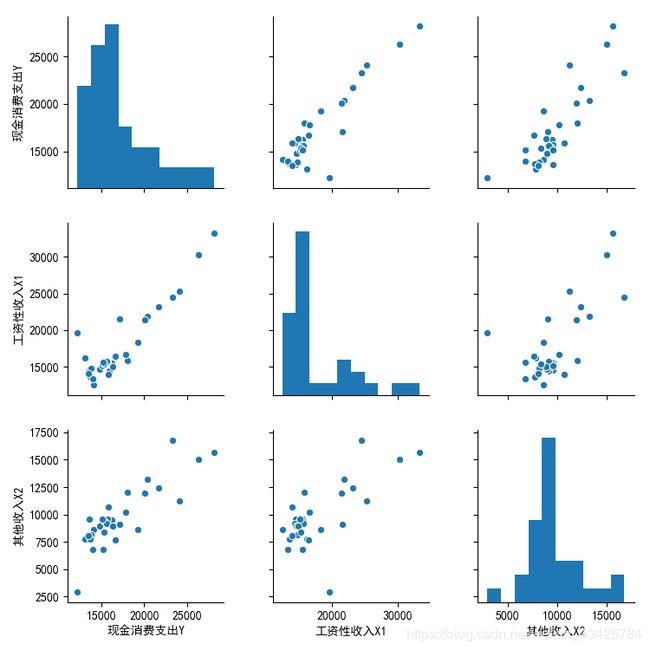
sns.pairplot(data.loc[:, ['现金消费支出Y', '工资性收入X1', '其他收入X2']])
# 显示图形
plt.show()
output:
OLS Regression Results
==============================================================================
Dep. Variable: 现金消费支出Y R-squared: 0.922
Model: OLS Adj. R-squared: 0.917
Method: Least Squares F-statistic: 166.6
Date: Sun, 26 May 2019 Prob (F-statistic): 2.84e-16
Time: 13:43:41 Log-Likelihood: -260.68
No. Observations: 31 AIC: 527.4
Df Residuals: 28 BIC: 531.7
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 2599.1455 827.342 3.142 0.004 904.412 4293.879
工资性收入X1 0.4865 0.058 8.448 0.000 0.369 0.604
其他收入X2 0.6017 0.104 5.772 0.000 0.388 0.815
==============================================================================
Omnibus: 1.082 Durbin-Watson: 1.915
Prob(Omnibus): 0.582 Jarque-Bera (JB): 0.556
Skew: 0.327 Prob(JB): 0.757
Kurtosis: 3.064 Cond. No. 8.50e+04
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 8.5e+04. This might indicate that there are
strong multicollinearity or other numerical problems.
模型检验:
H 0 : β j = 0 H_0:\beta_j=0 H0:βj=0
H 1 : β j 不 全 部 为 零 H_1:\beta_j不全部为零 H1:βj不全部为零拟合优度检验:
从回归估计来看,模型拟合较好,可决系数 R 2 = 0.922. R^{2}=0.922. R2=0.922.
F检验:
F值为166.6,查表得 F α ( k , n − k − 1 ) = 3.34 , 其 中 k = 2 , n = 31 , 显 然 有 F > F α ( k , n − k − 1 ) F_{\alpha}(k,n-k-1)=3.34,其中k=2,n=31,显然有F>F_{\alpha}(k,n-k-1) Fα(k,n−k−1)=3.34,其中k=2,n=31,显然有F>Fα(k,n−k−1),表明模型的线性关系在5%的显著水平下显著成立.所以拒绝原假设。
t检验:
∣ t 1 ∣ = 8.448 , ∣ t 2 ∣ = 5.772 , t α / 2 ( n − k − 1 ) = 2.048 \left|t_1\right|=8.448,\left|t_2\right|=5.772,t_{\alpha/2}(n-k-1)=2.048 ∣t1∣=8.448,∣t2∣=5.772,tα/2(n−k−1)=2.048
由 于 ∣ t ∣ > t α / 2 ( n − k − 1 ) , 所 以 拒 绝 零 假 设 . 由于\left|t\right|>t_{\alpha/2}(n-k-1),所以拒绝零假设. 由于∣t∣>tα/2(n−k−1),所以拒绝零假设.
综上可得中国2013年各地区人均现金消费支出与工资性收入、其他收入之间的关系为:
Y = 2599.1455 + 0.4865 X 1 + 0.6017 X 2 Y=2599.1455+0.4865X_1+0.6017X_2 Y=2599.1455+0.4865X1+0.6017X2
β 1 < β 2 \beta_1<\beta_2 β1<β2即其他收入对人均现金消费支出的贡献率要大于工资性收入。(此处有疑问,难道大家都靠外快过活吗?)
化为线性的非线性实例:
模型假设:
由Cobb-Dauglas生产函数 Y = A K β 1 L β 2 Y=AK^{\beta1}L^{\beta2} Y=AKβ1Lβ2,A代表既定的工程技术水平, β 1 \beta_1 β1、 β 2 \beta_2 β2分别为资本与劳动投入的产出弹性,当 β 1 + β 2 = 1 时 \beta_1+\beta_2=1时 β1+β2=1时,当大于1或小于1时,表明规模收益递增或递减。为了便于比较,下面将会对此模型进行线性变换,即假设2010年中国制造业各行业的总产出及要素投入的关系为:
Y = β 0 + β 1 log K + β 2 log L + μ Y=\beta_0+\beta_1\log K+\beta_2\log L+\mu Y=β0+β1logK+β2logL+μ
code:
data2 = pd.read_excel(r'C:\Users\仁义\Desktop\data.xlsx', sheet_name='Sheet2')
fit2 = sm.formula.ols(formula='np.log(工业总产值) ~ np.log(资本投入) + np.log(年均从业人员)', data=data2).fit()
sns.pairplot(data2.loc[:, ['工业总产值', '资本投入', '年均从业人员']])
print(fit2.summary())
plt.show()
output:
OLS Regression Results
==============================================================================
Dep. Variable: np.log(工业总产值) R-squared: 0.941
Model: OLS Adj. R-squared: 0.938
Method: Least Squares F-statistic: 286.3
Date: Sun, 26 May 2019 Prob (F-statistic): 7.86e-23
Time: 13:43:42 Log-Likelihood: -12.793
No. Observations: 39 AIC: 31.59
Df Residuals: 36 BIC: 36.58
Df Model: 2
Covariance Type: nonrobust
==================================================================================
coef std err t P>|t| [0.025 0.975]
----------------------------------------------------------------------------------
Intercept 1.8003 0.401 4.493 0.000 0.988 2.613
np.log(资本投入) 0.6778 0.081 8.344 0.000 0.513 0.843
np.log(年均从业人员) 0.2911 0.086 3.395 0.002 0.117 0.465
==============================================================================
Omnibus: 37.173 Durbin-Watson: 1.263
Prob(Omnibus): 0.000 Jarque-Bera (JB): 165.957
Skew: -2.018 Prob(JB): 9.18e-37
Kurtosis: 12.264 Cond. No. 75.3
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
模型检验:
H 0 : β j = 0 H_0:\beta_j=0 H0:βj=0
H 1 : β j 不 全 部 为 零 H_1:\beta_j不全部为零 H1:βj不全部为零
拟合优度检验:
从回归估计来看,模型拟合较好,可决系数 R 2 = 0.941. R^{2}=0.941. R2=0.941.
F检验:
F值为286.3,查表得 F α ( k , n − k − 1 ) = 3.26 , 其 中 k = 2 , n = 39 , 显 然 有 F > F α ( k , n − k − 1 ) F_{\alpha}(k,n-k-1)=3.26,其中k=2,n=39,显然有F>F_{\alpha}(k,n-k-1) Fα(k,n−k−1)=3.26,其中k=2,n=39,显然有F>Fα(k,n−k−1),表明模型的线性关系在5%的显著水平下显著成立.所以拒绝原假设。
t检验:
∣ t 1 ∣ = 8.344 , ∣ t 2 ∣ = 3.395 , t α / 2 ( n − k − 1 ) = 2.036 \left|t_1\right|=8.344,\left|t_2\right|=3.395,t_{\alpha/2}(n-k-1)=2.036 ∣t1∣=8.344,∣t2∣=3.395,tα/2(n−k−1)=2.036
由 于 ∣ t ∣ > t α / 2 ( n − k − 1 ) , 所 以 拒 绝 零 假 设 . 由于\left|t\right|>t_{\alpha/2}(n-k-1),所以拒绝零假设. 由于∣t∣>tα/2(n−k−1),所以拒绝零假设.
综上可得2010年中国制造业各行业的总产出及要素投入的关系为: Y = 1.8003 + 0.6778 log K + 0.2911 log L , 0.6778 + 0.2911 = 0.9689 Y=1.8003+0.6778\log K+0.2911\log L,0.6778+0.2911=0.9689 Y=1.8003+0.6778logK+0.2911logL,0.6778+0.2911=0.9689,以上结果表明,在2010年,中国工业总产出关于资本投入的产出弹性为0.6778,表明当其他因素不变时,工业的资本每增加1%,总产出将增加0.6778%,同样地,当其他因素不变时,劳动力投入每增长1%,总产出将增加0.2911%,可见,资本投入的增加对工业总产出的增长起到了更大的作用。
虚拟变量(哑变量):
在一些数据中,通常会有一些变量无法通过量化来进行处理,但是这些变量往往对模型结果产生较大的影响,所以,这类因素是无法被丢弃的,因此引入了“虚拟变量”,又叫做哑变量,来进行“量化处理”。下面我们将会以城镇居民为基准线对2013年中国农村与城镇居民家庭人均工资收入、其他收入和生活消费支出进行模型建立。
假设模型为:
Y = α 0 + α 1 X 1 + α 2 X 2 + C Y=\alpha_0+\alpha_1X_1+\alpha_2X_2+C Y=α0+α1X1+α2X2+C
code:
data3 = pd.read_excel(r'C:\Users\仁义\Desktop\data.xlsx', sheet_name='Sheet3')
fit3 = sm.formula.ols(formula='生活消费 ~ 工资收入 + 其他收入 + C(农村or城镇)', data=data3).fit()
print(fit3.summary())
output:
OLS Regression Results
==============================================================================
Dep. Variable: 生活消费 R-squared: 0.975
Model: OLS Adj. R-squared: 0.974
Method: Least Squares F-statistic: 758.1
Date: Sun, 26 May 2019 Prob (F-statistic): 1.81e-46
Time: 13:43:42 Log-Likelihood: -513.02
No. Observations: 62 AIC: 1034.
Df Residuals: 58 BIC: 1043.
Df Model: 3
Covariance Type: nonrobust
=====================================================================================
coef std err t P>|t| [0.025 0.975]
-------------------------------------------------------------------------------------
Intercept 1783.7377 345.728 5.159 0.000 1091.687 2475.788
C(农村or城镇)[T.城镇居民] 140.8608 483.598 0.291 0.772 -827.166 1108.888
工资收入 0.5477 0.039 13.978 0.000 0.469 0.626
其他收入 0.5589 0.073 7.666 0.000 0.413 0.705
==============================================================================
Omnibus: 0.360 Durbin-Watson: 1.733
Prob(Omnibus): 0.835 Jarque-Bera (JB): 0.086
Skew: 0.082 Prob(JB): 0.958
Kurtosis: 3.079 Cond. No. 6.19e+04
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 6.19e+04. This might indicate that there are
strong multicollinearity or other numerical problems.
模型检验:
H 0 : β j = 0 H_0:\beta_j=0 H0:βj=0
H 1 : β j 不 全 部 为 零 H_1:\beta_j不全部为零 H1:βj不全部为零
拟合优度检验:
从回归估计来看,模型拟合较好,可决系数 R 2 = 0.975. R^{2}=0.975. R2=0.975.
F检验:
F值为758.1,查表得 F α ( k , n − k − 1 ) = 4.16 , 其 中 k = 3 , n = 62 , 显 然 有 F > F α ( k , n − k − 1 ) F_{\alpha}(k,n-k-1)=4.16,其中k=3,n=62,显然有F>F_{\alpha}(k,n-k-1) Fα(k,n−k−1)=4.16,其中k=3,n=62,显然有F>Fα(k,n−k−1),表明模型的线性关系在5%的显著水平下显著成立.所以拒绝零假设。
t检验:
∣ t 1 ∣ = 0.291 , ∣ t 2 ∣ = 13.978 , , ∣ t 3 ∣ = 7.666 , t α / 2 ( n − k − 1 ) = 2.010 \left|t_1\right|=0.291,\left|t_2\right|=13.978,,\left|t_3\right|=7.666,t_{\alpha/2}(n-k-1)=2.010 ∣t1∣=0.291,∣t2∣=13.978,,∣t3∣=7.666,tα/2(n−k−1)=2.010
由 于 ∣ t ∣ > t α / 2 ( n − k − 1 ) , 所 以 拒 绝 零 假 设 . 由于\left|t\right|>t_{\alpha/2}(n-k-1),所以拒绝零假设. 由于∣t∣>tα/2(n−k−1),所以拒绝零假设.
综上可得2013年中国农村与城镇居民家庭人均工资收入、其他收入和生活消费支出的关系为:
Y = 1783.7377 + 0.5477 X 1 + 0.5589 X 2 + 140.8608 城 镇 居 民 Y=1783.7377+0.5477X_1+0.5589X_2+140.8608城镇居民 Y=1783.7377+0.5477X1+0.5589X2+140.8608城镇居民,
以上结果表明,当其他因素不变时,中国城镇居民平均消费支出比农村居民平均消费水平多140.8608元。
因变量预测:
有时建立完模型并对其进行检验后,还需观察实际值和预测值具体情况,以确定模型的可用性。
code:
data4 = pd.read_excel(r'C:\Users\仁义\Desktop\data.xlsx', sheet_name='Sheet1')
train, test = model_selection.train_test_split(data4, test_size=0.2, random_state=1234)
fit4 = sm.formula.ols(formula='现金消费支出Y ~ 工资性收入X1 + 其他收入X2', data=train).fit()
test_X = test.drop(labels='现金消费支出Y', axis=1)
pred = fit4.predict(exog=test_X)
print('对比预测值和实际值:\n', pd.DataFrame({'prediction': pred, 'real': test.现金消费支出Y}))
output:
对比预测值和实际值:
prediction real
7 13874.648201 14161.7
10 25068.272118 23257.2
4 16645.508042 19249.1
1 21539.239415 21711.9
29 15077.077324 15321.1
8 28477.482744 28155.0
3 15073.999588 13166.2
由预测值和实际值对比可以看出,有的预测值和实际值相差比较大,但总体上来说预测值与实际值比较接近,也就一定程度上说明了这个模型的可用性。