论文《A Cost-Effective Single-Shot Structured Light System for 3D Shape Measurement》学习

2019SCI(二区)

Abstract

单镜头三维形状测量技术由于适用于动态测量而引起了广泛的研究。在本研究中，我们提出一种成本效益高的单镜头结构光系统 cost-effective single-shot structured light system（CES-SLS），利用彩色摄影机和普通投影仪进行三维形状测量。单色相机借助于两个平面镜和一个等腰直角镜实现双目视觉。普通投影仪采用单镜头彩色随机散斑图(CRSP)对物体进行编码。用RGB图像子集的时空相关代替了传统的灰度图像子集的空间相关，得到了稠密对应点dense corresponding points(DCP)。提出了一种基于二次形状函数的逆合成高斯牛顿 (IC-GN)迭代法求解亚像素对应点 (CP)的方法。在此基础上，提出了一种几何恢复方法，通过最小化重投影误差来计算三维点。实验结果表明，该算法在测量精度和噪声鲁棒性方面都优于单镜头随机散斑图法和曲线拟合亚像素法。此外，几何方法中每个三维点的再投影误差都比传统的中点小。
关键字： 结构光系统，立体视觉，单镜头，颜色随机斑纹图案，三维形状测量。

I、Introduction And Related Works

广泛使用的结构光系统(SLS)通常由立体视觉和投影仪组成，因为它易于使用。立体视觉是基于三角测量原理的三维测量技术。利用立体视觉进行三维测量的主要挑战是定位高精度的DCP，因为均匀图像之间往往没有足够的特征。利用结构化光方法对物体[1]-[4]的表面进行编码，是解决这一问题的可靠方法。在[5]、[6]中给出了各种编码策略的概述。其中，相移基条纹投影轮廓术(FPP)是最常用的[7]编码方案，因为它可以通过低计算强度获得高精度的DCP。然而，对于基于相移的FPP来说，单次编码测试对象是不够的。另一方面，当使用多镜头RSP对测试对象进行编码时，也可以通过时间或时空相关来导出精确的DCP[8]、[9]。值得注意的是，RSP在本研究中指的是单色RSP。然而，单次发射的RSP可能不足以定位高精度的DCP。此外，多镜头FPP和多镜头RSP方法不适用于运动物体的测量，除非采用包含严格同步的高速摄像机和投影仪的昂贵系统，并假设物体在相邻帧内几乎是静止的。在这项研究中，我们提出了一个用于三维轮廓重建的CES-SLS。单色相机在两个平面镜和一个等腰直角镜的辅助下可以实现彩色立体视觉。一个单镜头的CRSP被投射到一个普通的投影仪上对物体进行编码。该方法适用于动态测量，即使彩色相机的帧率较低。本文的研究工作及意义如下:

A. Single-Lens Stereo Vision

为了解决传统双目系统中测量系统的仿真问题，降低硬件成本，避免系统的同步性问题，人们尝试将单目相机作为立体视觉[10]-[19]来使用。通过使用适当设计的光学适配器，可以在传感器平面上对对象的两个不同视图进行成像。每个视图在传感器平面的一半上成像，并且在传感器平面上的视图之间没有重叠。光适配器可以有多种配置，即、两个平面镜[10]-[13]、两个平面镜和一个分束器[14]、两个平面镜和一个棱镜[15]、四个平面镜[16]、一个衍射光栅[17]、一个双棱镜[18]。对于使用两面平面镜[10]-[13]的单镜头立体视觉，虽然简单紧凑，但也存在基线长度小、立体角度小的缺点，而立体角度是两个虚拟相机中心线之间的夹角。对于其他单镜头立体视觉系统[14]-[18]，基线长度和立体角度可以安排在较大的范围内。然而，在这些系统中，[14]、[15]、[18]的主要缺点是光路中不可避免的折射。在我们之前的工作中，我们提出了一个单色相机立体视觉系统[19]使用两个平面镜和一个二色滤光片。采用双色滤光片，利用光的波长来分离不同的视图。因此，不同的视图可以被彩色相机的不同通道捕获。

B. Single-Shot SLS

由于单镜头SLS[21] -[24]适用于运动目标的测量，因此得到了广泛的研究。相关工作可分为(1)基于傅里叶变换(FT-)的FPP、(2)彩色编码的FPP、(3)二维空间小模式编码 和 (4)RSP投影。傅里叶变换(FT - fpp)是一种利用傅里叶变换(FT)及其逆变换[25]、[26]实现相位解调的单镜头条纹模式。然而FT-FPP不适合测量纹理相对复杂的物体，限制了其应用。在彩色编码的FPP方面，例如，Budianto等人的[27]，[49]提出了一种具有不同相移的单镜头三条纹图案。然后用传统的三步相移算法进行相位反演。提出了一种将彩色条纹嵌入正弦条纹图的方法。相位由傅立叶变换(FT)得到，颜色编码带用于识别不连续情况下的条纹顺序。彩色FPP的主要限制是不同通道之间的串扰。它对反演阶段的精度有很大影响。在二维空间微缩模式中，可以使用单镜头网格或点模式对对象[29]-[33]进行编码。CP在网格或点的帮助下被定位。为了提高鲁棒性，采用了更复杂的模式对对象[34]-[37]进行编码。然而，需要许多像素来生成一个健壮的迷你模式，特别是当模式很复杂的时候。要投影大量的小图案，需要高分辨率的投影仪。此外，当一个小图案投射到对象上时，它将覆盖一个相对较大的区域。因此，很难通过单次拍摄的2D空间小模式获得DCP[31]。RSP投影可以克服二维空间小模式编码的局限性。当使用单镜头RSP对目标进行编码时，可以通过空间相关[38]-[40]定位DCP。然而，单次发射的RSP不能保证精度。虽然多点RSP可以提高精度[8]、[9]、[20]，但它们不适合于动态测量。最近，单次发射CRSP的三维形状测量方法被报道[41]，[42]。单镜头CRSP兼有单发RSP和多镜头RSP的优点。利用单镜头CRSP和时空相关技术可以定位出相对高精度的DCP。因此，本研究使用单镜头CRSP编码测试对象。

C.The Contributions of This Study

提出了一种基于CS-SLS的三维形状测量方法。将结构光方法引入单透镜立体视觉系统的研究很少。在这项工作中，我们将CRSP投影技术引入到单色相机立体视觉系统中。它的优点是:(a)单色光相机作为彩色双目视觉系统。由于散斑的尺寸相对于二维空间的小图形非常小，因此散斑投影不需要高分辨率投影仪。与广泛使用的由双目视觉和高分辨率投影仪组成的单镜头SLS相比，由彩色摄像机和普通投影仪组成的系统成本低。在提议的系统中也没有同步问题。另外，CES-SLS的校准非常简单，不需要校准投影仪。然而，由于[10]-[13]具有相似的结构，使得单色相机立体视觉系统的镜面结构的新颖性并没有被提出。(b)用RGB图像子集的时空相关代替单色图像子集的空间相关，可以得到精度更高的CP。©利用数字图像相关区域的二阶形状函数IC-GN迭代法求解亚像素CP，并与[41]中的五点二次曲线拟合方法进行比较。(d)提出了一种几何三维重建方法来计算再投影误差最小的三维位置。将该方法恢复的每个三维点的再投影误差与传统中点的再投影误差进行了比较。由于[50]中的反投影方法，使得该三维重建方法的新颖性不强。

本文组织如下。第二部分对所提出的CES-SLS进行了详细的描述。在第三节中，对所提系统的有效性进行了验证。第四部分给出了结论。

II. The Proposed CES-SLS

该方法包括四个步骤。首先，提出了一种生成均匀CRSP的简单方法。其次，给出了所提出的CES-SLS的结构，并进行了粗搜索，得到了初始CP。接下来，利用二阶形状函数的IC-GN迭代法对CP进行了细化。最后，提出了一种几何三维重建方法，通过最小化再投影误差来计算三维位置。这些步骤将在下面的小节中详细讨论。

A. CRSP Generation

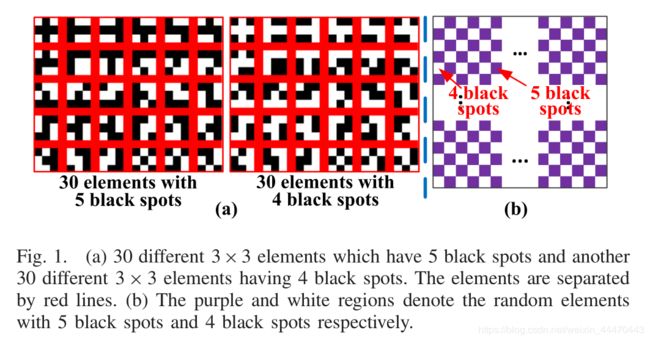
CRSP对准确定位DCP非常重要。散斑图案应满足以下几个要求:，均匀随机，体积小，图像对比度高。散斑图像的大小应与所选投影仪的分辨率相同。为了保证高对比度，散斑图像应该是二进制的。在本研究中，我们首先将散斑图像分成3×3个元素。在每个3×3个元素中，4或5个像素的值设为0，其余设为1。在图中，像素值0由黑点表示。图1(a)显示了30个不同的3×3元素，它们有5个黑点，另外30个不同的3×3元素，它们有4个黑点。在散斑图像中，5个黑点和4个黑点的元素依次出现，每个元素从30个元素中随机选取，如图1(b)所示。紫色区域表示有5个黑点的随机元素，白色区域表示有4个黑点的随机元素。在生成CRSP图像时，可以按照图1(b)的方式设置红色通道散斑图像。绿色通道图像,图1中的白色区域(b)将代表随机元素5黑色斑点和紫色区域表示随机元素4黑色的斑点,然而,在蓝色通道图1(b)中的白色区域表示随机元素4黑色的斑点和紫色区域表示随机元素5黑色点同样的红色通道。该方法产生的三个散斑图满足上述要求。此外，由于彩色相机的R、G和B通道的光谱响应通常不同，为了使拍摄的彩色图像的R、G和B通道尽可能具有相同的对比度，我们可以调整彩色相机每个通道的增益和投影RGB图像每个通道的强度，如Eq.(1)所示。

$$I_{RGB}=\{I_R\ast C_1；I_G\ast C_2；I_B\ast C3\}(1)$$
其中$I_{RGB}$表示投影的CRSP映像。$I_R,I_G$和$I_B$表示它的三个二进制通道，$C_1、C_2$和$C_3$表示它们相应的强度。图2示出当$C_1、C_2$和$C_3$分别被设置为255、210和210时生成的CRSP图像。

B. The Configuration of CES-SLS and Coarse Searching by Spatial-Temporal Correlation

所提出的CES-SLS的结构如图3(a)所示。它由一个彩色摄像机、一个等腰直角镜、两个平面镜和一个普通投影仪组成。借助于两个平面镜和一个等腰直角镜，一个单色相机可以从不同的角度捕捉到一个测试对象的两个视图，但每个视图只能在传感器平面的一半上成像。句话说，镜子可以创建两个虚拟彩色相机:一个虚拟左彩色相机和一个虚拟右彩色相机。由于这两个虚拟彩色相机来自于同一个彩色相机，所以它们是高度同步的，在本文提出的CES-SLS中不存在同步问题。因此，捕获系统很简单。虚拟彩色摄像机捕捉到的左右两侧图像均为同质图像。图4为CES-SLS捕获的彩色图像。此外，通过设置两个平面镜的位姿，可以在较大范围内调节单透镜彩色立体视觉的基线长度和立体角度，且两条光路不存在折射问题。上面讨论的CRSP是使用普通投影仪投射的。值得注意的是，在我们之前的工作[19]中，不同的视图是通过彩色相机的不同通道，借助于二色滤光片来捕捉的。因此，CES-SLS中单镜头彩色立体视觉的原理与我们之前的工作不同。

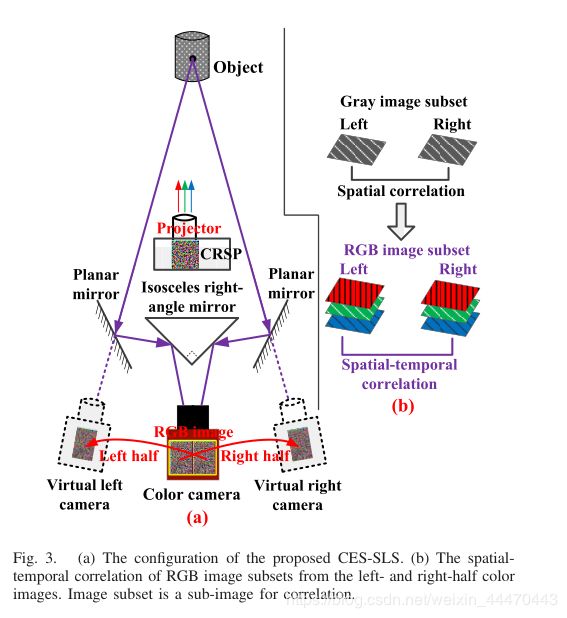
传统上采用单镜头RSP对测试对象进行编码，采用单色相机进行图像捕获。通过灰度图像子集的空间相关性，可以定位出DCP。在这项研究中，一个单镜头的CRSP被用来对物体进行编码，然后被一个彩色相机捕获。通过三层图像子集(RGB图像子集)的时空相关性搜索DCP，如图3(b)所示。因此，与传统方法相比，用这种方法定位的DCP应该更准确、更可靠。利用零均值归一化方差平方和(ZNSSD)对左半彩色图像和右半彩色图像的RGB图像子集进行关联，如式(2)所示。
$$Corr=\sum _{k=1}^3\sum _{i=-M}^M\sum _{j=-N}^N\{{\omega }_k[\frac{f(x_i,y_j,k)-{\overline{f}}_k}{{\sigma }_k^f}-\frac{g(x_i^{\ast },y_j^{\ast },k)-{\overline{g}}_k}{{\sigma }_k^g}{]}^2\}(2)$$
其中，$f(x_i,y_j,k)$表示左侧RGB子集的通道k中$(x_i,y_j)$处的像素强度。$g(x_i^{\ast },y_j^{\ast },k)$表示右RGB子集k通道中$(x_i^{\ast },y_j^{\ast })$处的像素强度。${\overline{f}}_k$和${\overline{g}}_k$分别为它们在通道k中的平均像素强度。${\sigma }_k^f$和${\sigma }_k^g$分别为通道k的标准差。${\omega }_1$，${\omega }_2$和${\omega }_3$分别是分配给R、G和B通道的权重。RGB子集的大小为(2M + 1)×(2N + 1)×3。为了有效地搜索右半彩色图像中的CP，只需检查极线上的像素即可。在极线上Corr最小的像素可以看作是初始CP，如图4所示，$P_L$是左半彩色图像中的一个兴趣点(POI)。它在右半图像中的$CP$ $P_R$在极线上。

C. Iteration to Obtain Sub-Pixel CP

由上述推导出的初始CP不够准确。高斯拟合和抛物面拟合是目前常用的初始CP优化方法。例如，在[41]中，我们使用五点二次曲线拟合的方法来求出亚像素CP，下面我们简单地用“曲线拟合”来表示“五点二次曲线拟合”的方法。在数字图像相关领域，广泛采用IC-GN迭代法[43]获得亚像素精度。在不同视图的图像子集之间存在形状变化。由于由式(3)表示的二阶形状函数可以用来描述比一阶形状函数[44]-[46]更复杂的形状变化，因此在本研究中，我们引入二阶形状函数IC-GN迭代法来细化初始CP。式中，IC-GN 2表示具有二阶形状函数的IC-GN。在实验中比较[41]和IC-GN 2曲线拟合的性能。式(3)是表示二阶形状函数的翘曲函数。其中p为变形参数：$p=\{u,u_x,u_y,u_{xx},u_{xy},u_{yy},v,v_x,v_y,v_{xx},v_{xy},v_{yy}\}$。warp函数W对p的导数为：$\frac{\partial W}{\partial p}=(1,x,y,\frac{1}{2}{x}^2,xy,\frac{1}{2}{y}^2,0,0,0,0,0,0;0,0,0,0,0,0,1,x,y,\frac{1}{2}{x}^2,xy,\frac{1}{2}{y}^2)$。通过在式(2)中引入warp函数，将Corr表示为式(4)，通过迭代更新p最小化Corr。在每次迭代中，增量$\Delta p$由Eq.(5)计算，然后更新W，直到Eq.(8)收敛。


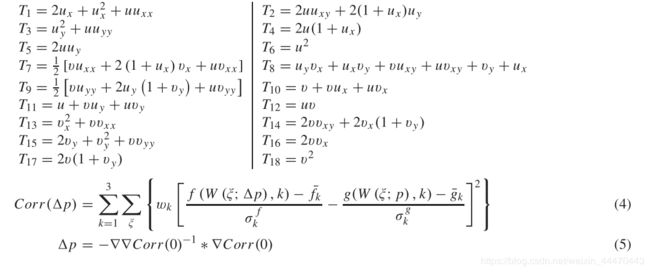
其中$\xi$表示像素在图像子集中的位置。图像子集的中心是(0,0)。−M ≤ x ≤ M,−N ≤ y ≤ N。(4)和(5)给出$T_1-T_{18}$,如图所示在前一页的底部,在∇Corr(0)是一阶导数Corr。∇∇Corr(0)是一个hessian矩阵及其大小12×12。它们可以用Eqs来计算。(6)、(7)分别为。

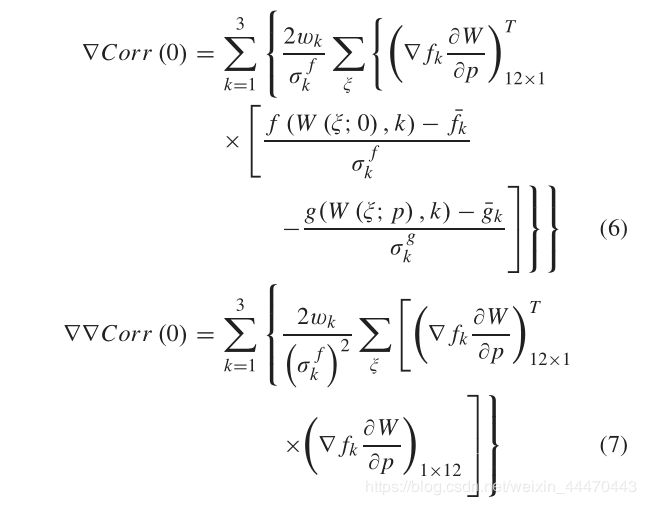
其中$\nabla f_k$为左半边RGB图像子集k通道的梯度向量：$\nabla f_k=(\frac{\partial f_k}{\partial x},\frac{\partial f_k}{\partial y})$。它可以通过Sobel函数得到。

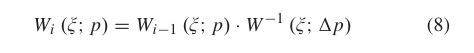
其中i为迭代次数。

收敛准则是$\Delta p$< 0.005，由式(9)表示。当迭代次数大于20时，表示迭代失败。

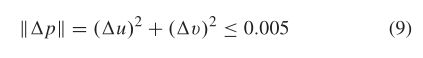
初始CP与收敛p的(u, v)之和为亚像素CP。

D. Geometrical 3D Reconstruction by Minimizing a Re-Projection Error

在找到亚像素CP后，利用三角法原理可以恢复三维位置。如图5所示，$q_L$是在左半幅图像中选择的POI, $q_R$是在右半幅图像中选择的CP。事实上，q R中的噪声是不可避免的，校准误差也是不可避免的。结果，这两条视线$\overline{O_L{q}_L}$和$\overline{O_R{q}_R}$总是不相交于一点。在这种情况下，3D点Q应该在$\overline{O_R{q}_R}$和$\overline{O_L{q}_L}$之间的最短线段上。统计上，在三维形状测量中，重建的三维点以最小的再投影误差为最优。本文提出一种简单的几何方法来恢复具有最小再投影误差的三维位置。首先，将虚拟左相机坐标系作为世界坐标系。OL和OR的各自位置为$[0,0,0{]}^T$和$-R^{-1}t$。基于摄像机投影模型的Eq.(10)可以计算出$O_L{q}_L$和$O_R{q}_R$的单位向量$u_L$和$u_R$。假设$\overline{O_L{Q}_R}$是$\overline{Q_R{q}_R}$和$\overline{O_L{q}_L}$之间最短的线段。QL和QR的坐标可以分别用$P_Q^L=||O_L{Q}_L||u_L$和$P_Q^R=-R^{-1}t+||O_R{Q}_R||$表示。然后根据最小二乘法，令$P_Q^L=P_Q^R$，如式(11)所示。一旦公式(12)计算出$||O_L{Q}_L||$和$||O_R{Q}_R||$，就可以计算出$P_Q^L$和 $P_Q^R$。3D点Q的重投影误差X由式(13)定义。我们试着找到有最小重新投影误差X的Q。当$Q_R$和$Q_L$的坐标确定后，得到了$q_L^m$和$q_R^m$的投影点。然后可以得到欧几里德距离$D_L^M=||q_L-q_L^m||$和$D_R^M=||q_R-q_R^m||$。我们定义$||Q_{L}Q||=\lambda ||Q_L{Q}_R||$。假设$\overline{q_L{Q}_L^m}//\overline{Q_{L}B}$。因此，$\frac{||Q_{L}A||}{||Q_{L}B||}=\frac{||q_L{q}_L^{\prime }||}{||q_L{q}_L^m||}$。此外，由于$||Q_L{Q}_R||\ll ||O_L{Q}_R||$和$||Q_L{Q}_R||\ll ||O_L{Q}_L||$；$\angle Q_L{O}_L{Q}_R$非常小并且$\overline{AQ}$几乎与$\overline{B{Q}_R}$平行。因此，$\frac{||Q_{L}A||}{||Q_{L}B||}\approx \frac{||Q_{L}Q||}{||Q_L{Q}_R||}=\lambda$。因此$||q_L{q}_L^{\prime }||\approx \lambda ||q_L{q}_L^m||$。类似的，$||q_R{q}_R^{\prime }||\approx (1-\lambda )q_R{q}_R^m\cdot X^2$可以被之后的等式14表示。为了最小化X,我们令$\frac{d(x^2)}{d\lambda }=0$和$\lambda$由等式15计算出来。最后通过式(16)计算出Q的三维位置。值得注意的是如果λ= 0.5,Q是传统的中点[19],[48]。在实验中，我们将比较中点的重投影误差和几何方法得到的三维点的重投影误差。

其中$(x_l,y_l)$是$q_L$的坐标，$(x_r,y_r)$是$q_R$的坐标。$K_L$和$K_R$分别是虚左相机和虚右相机的固有矩阵。R和t表示虚拟左右摄像头之间的旋转和平移。


式(16)中重建的三维点在虚拟左相机坐标系中进行描述。然而，为了更清楚地说明被测形状，世界坐标系统通常建立在由式(16)导出的三维点拟合的平面上。设$(R_L,t_L)$为虚拟左相机坐标系与世界坐标系的位姿关系，则可以计算出世界坐标系中的位置$(X_Q^W,Y_Q^W,Z_Q^W)$通过

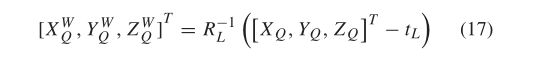
III. Experimental Validation

在实验中，首先进行标定，推导出虚拟左右摄像头各自的本征参数及其位姿关系。然后，我们通过比较来评估所提出的CES-SLS在标准球面(球面规，半径65mm)上的测量精度。测试了噪声的鲁棒性和图像子集大小的影响。接下来，使用所提出的系统对花卉模型进行轮廓测量。将用该方法计算出的三维点的重投影误差与传统的中点重投影误差进行了比较。此外，一个移动物体的形状也被测量。我们比较了提出的CES-SLS与使用两个单色相机的系统的准确性。分析了该方法的计算强度。最后，给出了两种失效情况。实验设置如图6(a)所示。测试对象与相机之间的距离取决于两个平面镜的姿态。在本实验中，距离约为80厘米。测试对象的大小取决于距离和焦距。对于大的物体，距离也应该增加。然后我们调整焦距，以适应左半边和右半边的图像。黑白相机为MG-282B/C，分辨率为1936×1458。该系统相当于一个分辨率为968×1458的虚拟双目视觉系统。虚拟基线的长度由两个平面镜的姿态决定。实验长度为151.354mm。投影仪为小型投影仪(Mileagea DLP Texas instrument)，分辨率为640×480。生成的CRSP如图2所示。彩色相机的RGB通道增益分别设置为2.2、1和1.42。Eq.(2)中对R, G, B通道赋值的权值分别为0.25，0.5和0.25。值得注意的是，安装平台上的常规螺栓孔与螺栓几乎可以在同一位置组装单色相机和彩色相机。

A. System Calibration

如图6(b)所示，采集了19张不同标定板姿态的RGB图像。将每个RGB图像转换为灰度图像，然后将其分为左右两幅图像。随后，利用MATLAB中的立体摄像机标定工具对系统进行标定。虚拟左右摄像头的固有参数为$(f_x^L,f_y^L,s_L,c_x^L,c_y^L,k_1^L,k_2^L)=(9057.2,8931.6,-131.95,-455.74,1229.6,-0.0369,-1.072)$和$(f_x^R,f_y^R,s_R,c_x^R,c_y^R,k_1^R,k_2^R)=(8931.7,8958.1,10.274,252.31,1141.7,0.1748,-19.462)$。外部参数为[0.9913,0.0261，−0.1288;−0.0272,0.9996, −0.0072;0.1286,0.0107,0.9916);平移向量为[- 150.03，- 1.694,19.90]。总的重投影误差为0.09像素。

B. Accuracy Evaluation

在标准球面上验证了所提出的CES-SLS的测量精度，如图7(a)所示。在这一节中，我们将使用单弹可编程控制器的系统的精度与使用单弹可编程控制器的系统的精度进行了比较。使用CRSP时，表示使用彩色相机;如果使用RSP，则意味着使用单色相机。此外，我们还比较了用于获得亚像素CP的曲线拟合[41]和IC-GN 2的精度。图像子集的大小为27×27。图7(b)和©分别显示了单色相机和彩色相机拍摄的灰度图像和彩色图像。可以看出，单色图像和RGB图像各通道的像素强度几乎服从随机分布。左半幅图像中黄色矩形包围的区域就是感兴趣区域(ROI)。在行和列中每三个像素密集地选择POI, POI的总数为20584。我们在右半图中搜索它们的CP。实验中CP密度很大。二维空间微模式编码方法几乎不可能获得如此高密度的CP。然后利用几何三维重建方法进行三维点的恢复。图7(d)为用该方法重建的三维球面。然后利用恢复后的三维点对球面进行拟合。在计算出的每个三维点上，总半径R和半径$r_i$都可以得到。用R与$r_i$之间绝对误差$\Delta r_i$的平均值$\overline{\Delta r}$和标准差${\sigma }^r$来评价测量精度。我们分别比较了用单镜头的RSP和CRSP的3D表面测量的统计误差($\overline{\Delta r}$和${\sigma }^r$)。此外，还比较了两种情况下 (a)对[41]曲线拟合得到亚像素CP;(b)亚像素CP由IC-GN 2得到。他们的统计误差($\overline{\Delta r}$和${\sigma }^r$)是记录在表1。结果表明:在两种情况下，采用单镜头CRSP的统计误差均小于采用单镜头RSP的统计误差;b) IC-GN 2的统计误差远小于曲线拟合的统计误差。因此，在这两种情况下，使用单镜头CRSP的系统的精度都高于使用单镜头RSP的系统；IC-GN2的精度也高于曲线拟合的精度[41]。

C. Noise Robustness Testing

在上述标准球面上，对单镜头CRSP和RSP系统的噪声鲁棒性进行了测试。左半幅图像保持不变，而右半幅图像则通过使用MATLAB函数imnoise添加高斯噪声$N(m,{\sigma }_G^2)$。平均值m是设置为0,而标准差${\sigma }_G$变化从0到0.07的步长0.005。图8为加入高斯噪声后右半部分图像的平均绝对误差$\overline{\Delta r}$。可以看出,(a)的平均绝对误差$\overline{\Delta r}$增加${\sigma }_G$的增量;(b)分别通过曲线拟合和$IC-G{N}_2$得到亚像素CP时，$\overline{\Delta r_M}$均比$\overline{\Delta r_C}$增长快;©曲线拟合的rr均明显高于IC-GN 2。因此，所提出的CSE-SLS系统的噪声鲁棒性要高于单点RSP系统;IC-GN 2的噪声鲁棒性优于曲线拟合。

D. The Effect of the Size of Image Subset

相关图像子集的大小对测量精度有很大的影响。在本节中，我们研究了使用单镜头CRSP和RSP时，图像子集的大小对系统精度的影响，如图9所示。图像子集的大小为l2，在第2步L从5变化到39。可以看出，1)平均绝对误差$\overline{\Delta r}$随图像子集大小的增大而减小;2)虽然随着图像子集大小的增加，单镜头RSP系统的平均绝对误差$\overline{\Delta r}$与单镜头RSP系统的平均绝对误差r之间的差异有所减小，但本文提出的系统的精度更高;3) IC-GN 2的精度明显高于曲线拟合的精度。在本试验中，随着图像子集大小的增加，精度提高的原因是图像子集中的结构化信息随着其大小的增加而增加，从而定位出精度更高的CP。(它也可以用来解释下表2中的结果。)实际上，根据经验，图像子集的大小建议为23×23到29×29。如果尺寸太大，计算强度太高;如果尺寸太小，结构化信息可能不足以找到准确的CP。在III.C和E小节中，尺寸的选择在推荐范围内。

E. Profile Measurement of a Flower Model

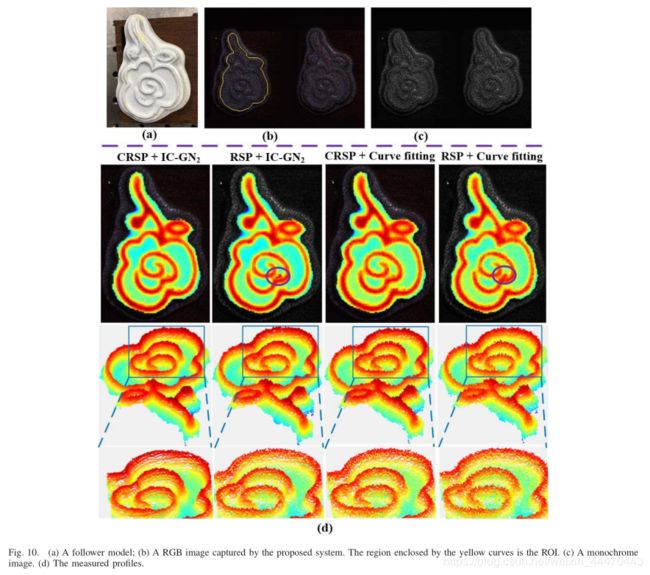
利用本文提出的CES-SLS测量图10(a)中的花模型轮廓。我们比较了在使用IC-GN 2和曲线拟合求亚像素CP的情况下，使用单镜头CRSP和单镜头RSP系统的性能。捕获到的RGB和mono- chrome图像如图10(b)和©所示。POI在行和列中每3个像素处选择一次。POI的总数是36811。通过将图像子集关联起来，可以得到高密度的CP。相关图像子集的大小为25×25。图10(d)分别采用单镜头CRSP和RSP对上述两种情况下的flower模型的实测剖面图。可以看出，当系统采用单镜头RSP时，有一个细节处理的不是很好，如紫色曲线所包围的区域所示。相比之下，在采用IC-GN 2和曲线拟合两种方法的情况下，单镜头CRSP法测得的系统轮廓均优于单镜头RSP法测得的系统轮廓，因为前者测得的轮廓更光滑，模糊/噪声更小。此外，IC-GN 2的拟合结果也优于曲线拟合结果。

F. Re-Projection Error Comparison

在利用双目视觉进行三维形状测量时，如果CP的坐标已经统计确定，则重建的三维点在再投影误差较小的情况下更加准确。在本节中，我们将所提出的几何方法所恢复的每个三维点的再投影误差与传统的中点的再投影误差进行了比较。CP来自于利用单镜头CRSP重建球面和花面的过程。如图11所示，所有POI的$R{E}_{Mid}$均大于对应的$R{E}_{Pro}:R{E}_{Mid}-R{E}_{Pro}>0$。这可能意味着，与传统的中点[19]、[48]相比，该方法重建的三维点具有更高的精度。

G. 3D Reconstruction of a Moving Fish Model

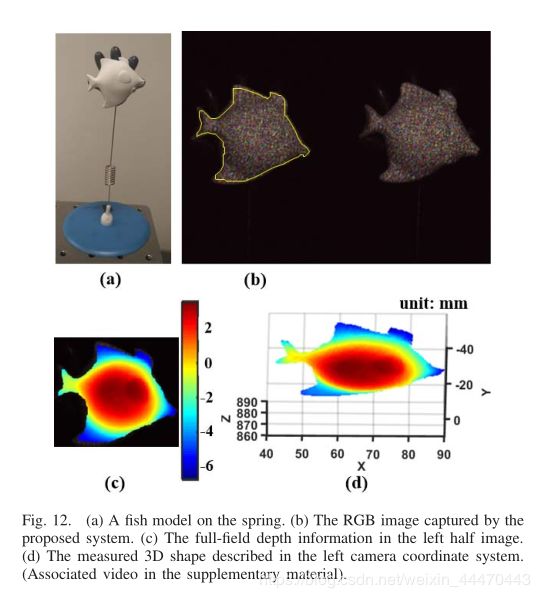
一个镜头就足以使该系统重建三维形状。因此，该系统可用于运动目标的形状测量。在本研究中，我们使用所提出的方法来测量一个动态的鱼模型。图12(a)显示了安装在弹簧上的鱼模型。
作用在fish模型上的瞬态力将使它移动。彩色相机的曝光时间设置为50ms。移动过程中在1秒内捕获20张RGB图像，CRSP在移动过程中保持不变。然后，我们利用每个RGB图像重建三维形状。图12(b)为采集到的一张RGB图像，图12(d)为左侧相机坐标系下的重构形状。制作视频，动态显示重建后的三维形状，如补充材料所示。这个移动过程在视频中重复了5次。值得注意的是，在视频的某些帧中，边缘上存在一些异常的重构三维点。

H. Accuracy Comparison With the System Using Two Monochrome Cameras and a Single-Shot RSP

为了进一步评价所提出的CES-SLS的性能，我们将其精度与使用两个单色相机和一个单镜头RSP的系统进行了比较。在图7(a)所示的标准球面上也对精度进行了评估。POIs的数量也是20584。我们已经调整了这个系统的配置，并且调整了两个摄像头的焦距，使物体适合视场。比较中考虑了不同大小的图像子集进行相关:11×11,21×21,31×31。表2显示了他们提出的CES-SLS和使用两个单色相机和一个单镜头RSP系统的平均绝对误差$\overline{\Delta r}$。很明显,当图像子集的大小是11×11日的准确性提出CES-SLS高于系统的使用两个单色相机,因为CP从时空相关性的RGB图像子集获得更准确的空间相关性比单色图像子集的大小如果图像子集很小。当图像子集的大小为21×21时，其精度非常接近。当图像子集的大小为31×31时，使用两个单色相机的系统的精度甚至高于提出的CES-SLS。可以用前者的分辨率高于后者来解释。因此，这一比较表明，如果图像子集的大小相对较小，所提出的CES-SLS的准确性甚至高于使用两个单色相机的系统。

I. Computation Intensity Analysis

该方法的一个缺点是，它的计算强度比传统的单镜头RSP方法要高。重建三维点的计算过程包括:a)时空相关搜索初始CP; b) IC-GN 2搜索亚像素CP; c)通过最小化重投影误差重建三维点的几何方法。通过比较，我们分析了计算三维点时每一步的计算过程。a)时空相关搜索初始CP:由于我们沿着极线搜索CP，并且可以根据之前计算的CP位置确定搜索点，所以在实验中每个POI的搜索点数量为5个。假设图像子集的大小为$L^2$。时空相关的时间复杂度为$T_P^1(L)=3\times 5L^2=15L^2=O(L^2)$；而传统RSP方法的空间相关时间复杂度为$T_C(L)=5L^2=O(L^2)$。前者的计算强度是后者的三倍。b) IC-GN 2得到亚像素CP: IC-GN 2的计算强度很大程度上取决于迭代次数。在实验中，平均迭代次数约为2.6次。虽然$IC-G{N}_2$的时间复杂度也约为$T^2=O(L^2)$，但IC-GN 2的计算强度要高于a)中的第一步。c)通过最小化再投影误差来重建三维点的几何方法:由于方程都是基于基本的微积分，所提出的地质信息处理方法的计算强度较低。计算强度与中点法基本一致。相对于a)和b)的计算强度可以忽略不计。实际上，借助于并行计算技术，如GPU，该方法可以实现实时测量。

J. Failure Cases of the Proposed CES-SLS

所提出的CES-SLS在某些情况下会失效。，测试对象表面近似镜面，如图13(a)所示;物体表面颜色较深，如图13(b)所示。值得注意的是，其他颜色编码的结构化光方法在这种情况下也会失败。

IV. Conclusion Remarks

在本研究中，我们使用彩色相机和普通投影仪制作了一个CES-SLS。单色相机在两个平面镜和一个等腰直角镜的辅助下可以实现双目视觉。用一种简单的方法生成均匀的CRSP，用单镜头对测试曲面进行编码。DCP是由RGB图像子集的时空相关性得到的。采用$IC-G{N}_2$对DCP进行了改进。提出了一种通过最小化再投影误差来计算三维点的几何三维重建方法。通过在标准球面、花模型和运动鱼模型上的实验，验证了该算法的有效性。结果表明:1)在测量精度和噪声鲁棒性方面，本文提出的单粒子可扩展自适应最小二乘系统的性能优于单粒子可扩展自适应最小二乘系统;2) $IC-G{N}_2$的精度也高于曲线拟合的精度;3)几何法计算的三维点的再投影误差小于常规中点;4)提出的CES-SLS能够对运动物体进行测量。

现有的单镜头SLS大多由双目视觉系统和相对高分辨率的投影仪组成。因此，由摄像机和普通投影仪组成的系统是经济有效的。没有必要校准投影仪，也没有同步问题，在提出的的系统中。该系统也存在一定的局限性。在单色摄像机中实现立体视觉;每个视图都在传感器平面的一半上成像，这会影响分辨率。但是，由于采用了$IC-G{N}_2$来寻找比曲线拟合精度更高的亚像素CP，因此在本系统中其效果可以得到一定的缓解。在测量运动物体时，投影仪可能会出现散焦现象。与其他颜色编码方法一样，该系统可能不适合测量高光或彩色物体。然而，尽管有局限性，我们相信所提出的系统可以用于各种应用。