机器学习实战笔记6——贝叶斯方法

任务安排

1、机器学习导论       8、核方法
2、KNN及其实现       9、稀疏表示
3、K-means聚类      10、高斯混合模型
4、主成分分析          11、嵌入学习
5、线性判别分析      12、强化学习
6、贝叶斯方法          13、PageRank
7、逻辑回归              14、深度学习

贝叶斯方法（Bayes Methods）

Ⅰ 先验概率与后验概率

      在贝叶斯统计推断论中，一个未确定数目的先验概率分布（一般简称为先验）是一种表达了某人对于该数目的信仰的一种概率分布，这种信仰是没有考虑到一些（当前的）证据的；

      先验概率即边缘概率，通俗点理解为“第六感”，它往往作为"由因求果"问题中的“因”出现的概率

      在贝叶斯推断中，一个随机事件的后验概率是指：当与事件相关的一些证据或背景也被考虑进来时的条件概率。“后验”在这个语境下指在考虑了与要被检验的特定事件相关的证据；

      后验概率即条件概率，即你收集证据以后，佐证了你的直觉，或是开始质疑直觉，是“由果溯因”问题中的"果"
      比如你开了一局王者荣耀，刚好在一楼，因为你每个位置的胜率都只有53%（先验概率），但是你心血来潮想玩打野，就在选下去的一刹那，二、三、四、五楼的队友都发出了胜率，打野73%、射手66%、中单65%、边路57%，为了团队，你忍辱负重，改选了一手辅助，你感觉，这把稳了，胜率>>53%（后验概率）
      这就是先验概率和后验概率的区别：先验概率基于已有知识对随机事件进行概率预估，但不考虑任何相关因素——$P(c)$。后验概率基于已有知识对随机事件进行概率预估，并考虑相关因素——$P(c|x)$

Ⅱ 贝叶斯公式

      贝叶斯方法是一种非常神奇，由后验概率求先验概率的方法，即科学地预知未来。其核心就是利用我们所熟知的——贝叶斯公式：$$P(c|x)=\frac{P(x,c)}{P(x)}=\frac{P(x|c)P(c)}{P(x)}$$      虽然贝叶斯公式很好用，但通常都是建立在，我们的题目是设计好了的情况下，但是实际生活中的问题，往往不会按我们期望的那样出现，贝叶斯公式也会有乏力的时候
      例①：以下是某门诊截至目前的问诊情况（某样本集，症状、职业都是该样本集的特征，疾病是决策结果（标签））

ID	症状	职业	疾病
1	打喷嚏	护士	感冒
2	打喷嚏	农夫	过敏
3	头疼	建筑工人	脑震荡
4	头疼	建筑工人	感冒
5	打喷嚏	教师	感冒
6	头疼	教师	脑震荡

      现在又来了第七个病人，是一个打喷嚏的建筑工人。请问他患上感冒的概率有多大？
由贝叶斯公式，我们可以很容易得到$$P(感冒|打喷嚏，建筑工人)=\frac{P(打喷嚏，建筑工人|感冒)P(感冒)}{P(打喷嚏，建筑工人)}$$$$P(感冒)=1/2$$$$P(打喷嚏，建筑工人)=P(打喷嚏)P(建筑工人)=\frac{1}{2}\times \frac{1}{3}=\frac{1}{6}$$      但是根据表格 $P(打喷嚏，建筑工人|感冒)$，我们求出来竟然是——0？，显然这不可能，那么单单靠贝叶斯公式是无法解决此问题了。
      那么，就出现了朴素贝叶斯

★Ⅲ 朴素贝叶斯（Naive Bayes）

      “朴素”是指：属性条件独立性假设
朴素贝叶斯分类器假设：
      所有特征条件独立于决策（特征独立性），（用到了数理统计里的极大似然估计）即
$$P(f_1,...,f_d|class)=\prod _{i=1}^{d}P(f_i|class)$$
      每个特征条件同等重要（特征均衡性）

      有了新的假设，那么我们可以接着解决上面的问题了
$$P(打喷嚏，建筑工人|感冒)=P(打喷嚏|感冒)P(建筑工人|感冒)=\frac{2}{3}\times \frac{1}{3}=\frac{2}{9}$$故最终答案$$P(感冒|打喷嚏，建筑工人)=\frac{\frac{2}{9}\times \frac{1}{2}}{\frac{1}{6}}=\frac{2}{3}$$这里特别注意一下，
$$P(A,B|C)=P(A|C)P(B|C)\nRightarrow P(A,B)=P(A)P(B)$$      能够成功求解该题分母的值仅仅是因为，根据实际生活情况我们可以知道，症状与职业是相互独立，与朴素贝叶斯分类器做的假设毫无关系，即假如症状与职业不相互独立，这题根据目前知识无法求解
      但是这仍然不妨碍我们引出朴素贝叶斯分类器的使用，顾名思义，“分类”，属于监督学习，所以我们实际应用中，只是为了与其他决策（标签）作比较，得出最有可能的标签，即我们的预测标签，故实际的概率值不是我们的目标，我们只需要得到分子的值，而分母的值大家都一样，对预测结果没有影响
      仍然拿上面那题举例，这次问，第七个病人是一个打喷嚏的建筑工人，他最有可能得什么病？
即比较 $P(感冒|打喷嚏，建筑工人)$、$P(过敏|打喷嚏，建筑工人)$、$P(脑震荡|打喷嚏，建筑工人)$ 的值，由贝叶斯公式变形后，分母均为 $P(打喷嚏，建筑工人)$，故只需比较分子 $P(打喷嚏，建筑工人|感冒)P(感冒)$、$P(打喷嚏，建筑工人|过敏)P(过敏)$、$P(打喷嚏，建筑工人|脑震荡)P(脑震荡)$ 的值就可以得出结论

例②（数值型朴素贝叶斯）：

性别	身高（英尺）	体重（磅）	脚掌（英寸）
男	6	180	12
男	5.92	190	11
男	5.58	170	12
男	5.92	165	10
女	5	100	6
女	5.5	150	8
女	5.42	130	7
女	5.75	150	9

      已知某人身高$6$英尺，体重$130$磅，脚掌$8$英寸，求该人的性别
由贝叶斯公式得到：$$P(性别|身高，体重，脚掌)=\frac{P(身高|性别)P(体重|性别)P(脚掌|性别)P(性别)}{P(身高)P(体重)P(脚掌)}$$      这里出现的难点就是，对于数值型，每一个新的数值，都是该特征新的一类，如果参照上一题的做法，求解起来就会显得非常复杂。
      这里采用朴素贝叶斯里的其中一种解决方法——高斯朴素贝叶斯（还有多元朴素贝叶斯，伯努利模型，暂时没用到，就先不提了）

高斯朴素贝叶斯
      如果要处理的是连续数据，一种通常的假设是这些连续数值为高斯分布（正态分布）。例如假设训练集中有一个连续属性$x$。我们首先对数据根据类别分类，然后计算每个类别中的$x$的均值和方差。令${\mu }_c$表示为$x$在$c$类上的均值，令${\sigma }_c^2$为$x$在$c$类上的方差。在给定类中某个值的概率$P(x=v|c)$，可以通过将$v$表示成均值为${\mu }_c$方差为${\sigma }_c^2$的正态分布，得到$P(x=v|c)=\frac{1}{\sqrt{2\pi {\sigma }_c^2}}{e}^{-\frac{(v-{\mu }_c{)}^2}{2{\sigma }_c^2}}$。

      处理连续数值问题的另一种常用的技术是通过离散化连续数值的方法（不会QUQ）。通常，当训练样本数量较少或精确的分布已知时，通过概率分布的方法是一种更好的选择。在大量样本的情形下离散化的方法表现更优，因为大量的样本可以学习到数据的分布。由于朴素贝叶斯是一种典型的用到大量样本的方法（越大计算量的模型可以产生越高的分类精度），所以朴素贝叶斯方法更多用到离散化方法，而不是概率分布估计的方法（虽然这里用到）。
      对于该题，求解出男性的身高满足均值是$5.855$，方差是$0.035$的正态分布，即 $P(身高|性别)\backsim N(\mu ,\sigma )$，得到$$P(身高|性别)=\frac{1}{\sqrt{2\pi \times 0.035}}{e}^{-\frac{(6-5.855{)}^2}{2\times 0.035}}$$      其他类似，最终就可以预测性别了！

Ⅳ 贝叶斯网络

定义：
      令 $G=(I,E)$ 表示一个有向无环图（拓扑图），其中 $I$ 代表图形中所有节点的集合，而 $E$ 代表有向连接线段的集合，且令 $X=(X_i{)}_{i\in I}$ 为其有向无环图中的某一节点 $i$ 所代表的随机变量，若节点 $X$ 的联合概率可以表示成:$$p(x)=\prod _{i\in I}p(x_i|x_{par(i)})$$      则称 $X$ 为相对于有向无环图 $G$ 的贝叶斯网络，其中 $par(i)$(parents) 表示节点 $i$ 之“因”。此外，对于任意的随机变量，其联合概率可由各自的局部条件概率分配相乘而得出，即$$p(x_1,...,x_k)=p(x_k|x_1,...,x_{k-1})p(x_{k-1}|x_1,...,x_{k-2})...p(x_2|x_1)p(x_1)$$      例：比如我们可能会经历过的，因为太久不玩某个游戏，被官方“删号了”，而它的决策机制就是基于贝叶斯网络

      弧上用条件概率 $P(被指向节点|指向节点)$表示权值（连接强度）
      连接两个节点的箭头代表此两个随机变量是具有因果关系，或非条件独立

贝叶斯网络的三种形式：
      对于一个$DAG$(有向无环图)$E$，引入$D-Separation$方法可以快速地判断出两个节点之间是否是条件独立，从而化简概率计算（$D-Separation$是一种用来判断变量是否条件独立的图形化方法）
形式1：$head-to-head$

      由图知 $P(a,b,c)=P(b)P(a)P(c|a,b)$
      由联合概率与各自局部条件概率的关系得出
$P(a,b,c)=P(c|a,b)P(a,b)=P(c|a,b)P(b|a)P(a)$
      联立可得 $P(a,b)=P(a)P(b)$
      即在 $c$ 未知的条件下，$a$、$b$被阻断(blocked)，是独立的，称之为$head-to-head$条件独立
      如形式1，可以求如下概率时得到化简：$P(a,b)=P(a)P(b)$，$P(a|b)=P(a)$，$P(b|a)=P(b)$

形式2：$tail-to-tail$

      由图知 $P(a,b,c)=P(c)P(a|c)P(b|c)$
      由联合概率与各自局部条件概率的关系得出
$P(a,b,c)=P(a,b|c)P(c)$
      联立得 $P(a,b|c)=P(a|c)P(b|c)$
      即在 $c$ 给定的条件下，$a$、$b$被阻断(blocked)，是独立的，称之为 $tail-to-tail$ 条件独立

形式3：$head-to-tail$

      由图知 $P(a,b,c)=P(a)P(c|a)P(b|c)$
      由联合概率与各自局部条件概率的关系得出
$P(a,b,c)=P(a,b|c)P(c)$     $P(a,c)=P(a)P(c|a)=P(c)P(a|c)$
      联立得 $P(a,b|c)=P(a|c)P(b|c)$
      即在 $c$ 给定的条件下，$a$、$b$被阻断(blocked)，是独立的，称之为 $head-to-tail$ 条件独立

      介绍的不详细，仅作了解，详细分析可看从贝叶斯方法谈到贝叶斯网络

Ⅴ 小结

      ● 通过估计条件概率来进行分类和推理
      ● 朴素贝叶斯假设每个特征是条件独立
      ● 将每个特征（属性）看作随机变量

今日任务

1.给定数据集，比较朴素贝叶斯和KNN的分类性能
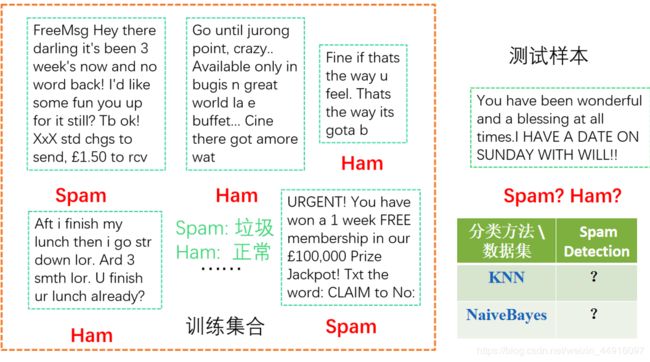
2.垃圾邮件过滤器（选做）

任务解决

1、可视化在上一篇博客机器学习实战笔记5——线性判别分析里写过了，这里学习一下朴素贝叶斯的调用即可（和KNN使用方法基本一致，用起来比较简单），注意一点，样本集一定要划分成训练集和测试集

from sklearn.datasets import load_digits
from sklearn import naive_bayes
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from myModule import clustering_performance
import numpy as np
import os
import cv2 as cv


# KNN分类器
def test_KNN(*data):
    X_train, X_test, y_train, y_test = data
    knn = KNeighborsClassifier()
    knn.fit(X_train, y_train)
    y_sample = knn.predict(X_test)
    print('KNN分类器')
    ACC = clustering_performance.clusteringMetrics1(y_test, y_sample)
    print('Testing Score: %.4f' % ACC)
    return ACC


# 高斯贝叶斯分类器
def test_GaussianNB(*data):
    X_train, X_test, y_train, y_test = data
    cls = naive_bayes.GaussianNB()  # ['BernoulliNB', 'GaussianNB', 'MultinomialNB', 'ComplementNB','CategoricalNB']
    cls.fit(X_train, y_train)
    # print('高斯贝叶斯分类器')
    print('贝叶斯分类器')
    print('Testing Score: %.4f' % cls.score(X_test, y_test))
    return cls.score(X_test, y_test)


path_face = 'C:/Users/1233/Desktop/Machine Learning/face_images/'
path_flower = 'C:/Users/1233/Desktop/Machine Learning/17flowers/'


# 读取Face image
def createDatabase(path):
    # 查看路径下所有文件
    TrainFiles = os.listdir(path)  # 遍历每个子文件夹
    # 计算有几个文件(图片命名都是以 序号.jpg方式)
    Train_Number = len(TrainFiles)  # 子文件夹个数
    X_train = []
    y_train = []
    # 把所有图片转为1维并存入X_train中
    for k in range(0, Train_Number):
        Trainneed = os.listdir(path + '/' + TrainFiles[k])  # 遍历每个子文件夹里的每张图片
        Trainneednumber = len(Trainneed)  # 每个子文件里的图片个数
        for i in range(0, Trainneednumber):
            image = cv.imread(path + '/' + TrainFiles[k] + '/' + Trainneed[i]).astype(np.float32)  # 数据类型转换
            image = cv.cvtColor(image, cv.COLOR_RGB2GRAY)  # RGB变成灰度图
            X_train.append(image)
            y_train.append(k)
    X_train = np.array(X_train)
    y_train = np.array(y_train)
    return X_train, y_train


X_train_flower, y_train_flower = createDatabase(path_flower)
X_train_flower = X_train_flower.reshape(X_train_flower.shape[0], 180*200)
X_train_flower, X_test_flower, y_train_flower, y_test_flower = \
    train_test_split(X_train_flower, y_train_flower, test_size=0.2, random_state=22)

digits = load_digits()
X_train_digits, X_test_digits, y_train_digits, y_test_digits = \
    train_test_split(digits.data, digits.target, test_size=0.2, random_state=22)

X_train_face, y_train_face = createDatabase(path_face)
X_train_face = X_train_face.reshape(X_train_face.shape[0], 180*200)
X_train_face, X_test_face, y_train_face, y_test_face = \
    train_test_split(X_train_face, y_train_face, test_size=0.2, random_state=22)

print('17flowers分类')
test_KNN(X_train_flower, X_test_flower, y_train_flower, y_test_flower)
test_GaussianNB(X_train_flower, X_test_flower, y_train_flower, y_test_flower)
print('Digits分类')
test_KNN(X_train_digits, X_test_digits, y_train_digits, y_test_digits)
test_GaussianNB(X_train_digits, X_test_digits, y_train_digits, y_test_digits)
print('Face images分类')
test_KNN(X_train_face, X_test_face, y_train_face, y_test_face)
test_GaussianNB(X_train_face, X_test_face, y_train_face, y_test_face)

效果图（$train:test=8:2$）

2、原理简单点理解就是，提供训练样本及其标签，$1$ 为 $spam$（垃圾邮件），$0$ 为 $ham$（正常邮件），生成语料库，然后输入测试样本时，根据语料库里提供的数据，计算该邮件中$spam$、$ham$单词出现的频率，求出该邮件是$spam$的概率，大于某我们设定的阈值，即预测它为$spam$
      核心代码老师基本都写完了然后给我们（文本转向量相关的知识还没有学，目前搞不定），我们主要就做个分类，老师给的库及垃圾邮件样本集已上传到个人资源里了可以下载
      因为以后可能自己也会写库，量多了，全放在和程序相同的目录下会看得眼花缭乱，这里最好自己封装起来之后直接import调用就好
路径如图所示

创建一个myModule文件夹，把自己写的.py文件放进去即可（_pycache_里的文件是调用时自动生成的，可以加快之后调用的速度）

主代码

from sklearn.metrics import confusion_matrix
import seaborn as sns
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
# 老师给的库
from myModule import clustering_performance
import myModule.EmailFeatureGeneration as Email

X, Y = Email.Text2Vector()
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size=0.2, random_state=22)
# print("X_train.shape =", X_train.shape)
# print("X_test.shape =", X_test.shape)


# 朴素贝叶斯
clf = GaussianNB()
clf.fit(X_train, y_train)
y_sample_bayes = clf.predict(X_test)
Bayes_ACC = clustering_performance.clusteringMetrics1(y_test, y_sample_bayes)
print("Bayes_ACC =", Bayes_ACC)

fig = plt.figure()
plt.subplot(121)
plt.title('Bayes')
confusion = confusion_matrix(y_sample_bayes, y_test)
confusion = confusion/X_test.shape[0]
# print(confusion)
sns.heatmap(confusion, annot=True, cmap='Blues', fmt='.3g')
plt.xlabel('Predicted label')
plt.ylabel('True label')

# KNN
knn = KNeighborsClassifier()
knn.fit(X_train, y_train)
y_sample_knn = knn.predict(X_test)
KNN_ACC = clustering_performance.clusteringMetrics1(y_test, y_sample_knn)
print("KNN_ACC =", KNN_ACC)

plt.subplot(122)
plt.title('KNN')
confusion = confusion_matrix(y_sample_knn, y_test)
confusion = confusion/X_test.shape[0]
sns.heatmap(confusion, annot=True, cmap='YlGn', fmt='.3g')
plt.xlabel('Predicted label')


plt.show()

老师给的代码（部分）
（EmailFeatureGeneration）

"""
@Author: Shiping Wang
@ Email: [email protected]
"""

from myModule import AdaboostNavieBayes as boostNaiveBayes
from sklearn import preprocessing
import numpy as np

path = 'C:/Users/1233/Desktop/Machine Learning/SpamEmailDetector/SpamEmailDetector/'


def Text2Vector( ):
    """
    return: feature matrix: nxd
            labels:  n x 1
    """

    ### Step 1: Read data 
    filename = path + 'emails/training/SMSCollection.txt'
    smsWords, classLabels = boostNaiveBayes.loadSMSData(filename)
    classLabels = np.array(classLabels)


    ### STEP 2: Transform the original data into feature matrix
    vocabularyList = boostNaiveBayes.createVocabularyList(smsWords)
    print("生成语料库！")
    trainMarkedWords = boostNaiveBayes.setOfWordsListToVecTor(vocabularyList, smsWords)
    print("数据标记完成！")
    # 转成array向量
    trainMarkedWords = np.array(trainMarkedWords)  ### Traning feature matrix N x d
    #print("The all feature matrix size is: ", trainMarkedWords.shape)
    
    return trainMarkedWords, classLabels

（AdaboostNaiveBayes）

path = 'C:/Users/1233/Desktop/Machine Learning/SpamEmailDetector/SpamEmailDetector/'


def textParser(text):
    """
    对SMS预处理，去除空字符串，并统一小写
    :param text:
    :return:
    """
    import re
    regEx = re.compile(r'[^a-zA-Z]|\d')  # 匹配非字母或者数字，即去掉非字母非数字，只留下单词
    words = regEx.split(text)
    # 去除空字符串，并统一小写
    words = [word.lower() for word in words if len(word) > 0]
    return words


def loadSMSData(fileName):
    """
    加载SMS数据
    :param fileName:
    :return:
    """
    f = open(fileName, 'rb')
    classCategory = []  # 类别标签，1表示是垃圾SMS，0表示正常SMS
    smsWords = []
    for line in f.readlines():
        linedatas = line.decode('utf-8').strip().split('\t')
        if linedatas[0] == 'ham':
            classCategory.append(0)
        elif linedatas[0] == 'spam':
            classCategory.append(1)
        # 切分文本
        words = textParser(linedatas[1])
        smsWords.append(words)
    return smsWords, classCategory


def createVocabularyList(smsWords):
    """
    创建语料库
    :param smsWords:
    :return:
    """
    vocabularySet = set([])
    for words in smsWords:
        vocabularySet = vocabularySet | set(words)
    vocabularyList = list(vocabularySet)
    return vocabularyList


def getVocabularyList(fileName):
    """
    从词汇列表文件中获取语料库
    :param fileName:
    :return:
    """
    fr = open(fileName)
    vocabularyList = fr.readline().strip().split('\t')
    fr.close()
    return vocabularyList


def setOfWordsToVecTor(vocabularyList, smsWords):
    """
    SMS内容匹配预料库，标记预料库的词汇出现的次数
    :param vocabularyList:
    :param smsWords:
    :return:
    """
    vocabMarked = [0] * len(vocabularyList)
    for smsWord in smsWords:
        if smsWord in vocabularyList:
            vocabMarked[vocabularyList.index(smsWord)] += 1
    return np.array(vocabMarked)


def setOfWordsListToVecTor(vocabularyList, smsWordsList):
    """
    将文本数据的二维数组标记
    :param vocabularyList:
    :param smsWordsList:
    :return:
    """
    vocabMarkedList = []
    for i in range(len(smsWordsList)):
        vocabMarked = setOfWordsToVecTor(vocabularyList, smsWordsList[i])
        vocabMarkedList.append(vocabMarked)
    return vocabMarkedList


def trainingNaiveBayes(trainMarkedWords, trainCategory):
    """
    训练数据集中获取语料库中词汇的spamicity：P（Wi|S）
    :param trainMarkedWords: 按照语料库标记的数据，二维数组
    :param trainCategory:
    :return:
    """
    numTrainDoc = len(trainMarkedWords)
    numWords = len(trainMarkedWords[0])
    # 是垃圾邮件的先验概率P(S)
    pSpam = sum(trainCategory) / float(numTrainDoc)

    # 统计语料库中词汇在S和H中出现的次数
    wordsInSpamNum = np.ones(numWords)
    wordsInHealthNum = np.ones(numWords)
    spamWordsNum = 2.0
    healthWordsNum = 2.0
    for i in range(0, numTrainDoc):
        if trainCategory[i] == 1:  # 如果是垃圾SMS或邮件
            wordsInSpamNum += trainMarkedWords[i]
            spamWordsNum += sum(trainMarkedWords[i])  # 统计Spam中语料库中词汇出现的总次数
        else:
            wordsInHealthNum += trainMarkedWords[i]
            healthWordsNum += sum(trainMarkedWords[i])

    pWordsSpamicity = np.log(wordsInSpamNum / spamWordsNum)
    pWordsHealthy = np.log(wordsInHealthNum / healthWordsNum)

    return pWordsSpamicity, pWordsHealthy, pSpam


def getTrainedModelInfo():
    """
    获取训练的模型信息
    :return:
    """
    # 加载训练获取的语料库信息
    vocabularyList = getVocabularyList(path + 'vocabularyList.txt')
    pWordsHealthy = np.loadtxt(path + 'pWordsHealthy.txt', delimiter='\t')
    pWordsSpamicity = np.loadtxt(path + 'pWordsSpamicity.txt', delimiter='\t')
    fr = open(path + 'pSpam.txt')
    pSpam = float(fr.readline().strip())
    fr.close()

    return vocabularyList, pWordsSpamicity, pWordsHealthy, pSpam


def classify(pWordsSpamicity, pWordsHealthy, DS, pSpam, testWordsMarkedArray):
    """
    计算联合概率进行分类
    :param testWordsMarkedArray:
    :param pWordsSpamicity:
    :param pWordsHealthy:
    :param DS:  adaboost算法额外增加的权重系数
    :param pSpam:
    :return:
    """
    # 计算P(Ci|W)，W为向量。P(Ci|W)只需计算P(W|Ci)P(Ci)
    ps = sum(testWordsMarkedArray * pWordsSpamicity * DS) + np.log(pSpam)
    ph = sum(testWordsMarkedArray * pWordsHealthy) + np.log(1 - pSpam)
    if ps > ph:
        return ps, ph, 1
    else:
        return ps, ph, 0

效果图（KNN跑起来明显要慢不少，但是效果更好）
（$train:test=8:2$）