在前面的两篇博客中,我们介绍了DNN(深度神经网络)并使用keras实现了一个简单的DNN。在这篇博客中将介绍CNN(卷积神经网络),然后在下一篇博客中将使用keras构建一个简单的CNN,对cifar10数据集进行分类预测。
CNN简介
我们可以想一个例子,假如我们现在需要对人进行识别分类,根据我们人类的思维,我们肯定是比较他的是不是一样的,是不是一样大小,是不是双(or 三)下巴。换句话来说,我们的判断标准是一个可视的范围。
CNN就是受到了人类视觉神经系统的启发,使用卷积核来代替人类中的视野,这样既能够降低计算量,又能够有效的保留图像的特征,同时对图片的处理更加的高效。我们可以想一想前面介绍的DNN网络,它是将一个一个的像素点进行计算的,毋庸置疑,这样必然会带来参数的膨胀,比如说cifar-10中一张32*32*3的图像,第一个隐藏层的中的单个神经元就有\(32 \times 32 \times 3 = 3072\)个权重,似乎挺小的,但是如果图片的像素再大一点,则参数会飞速猛增,同时参数增加的同时就会导致过拟合。
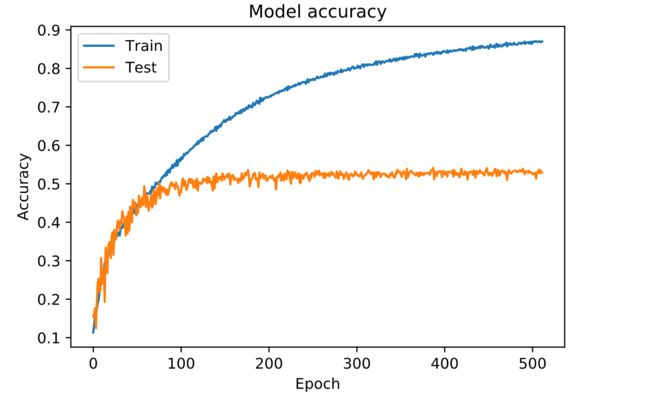
下图是我使用DNN网络去训练cifar-10得到的结果,可以明显的看到过拟合:
而CNN就是将DNN中复杂的问题简单化(实际上更复杂,但是参数简单化了)。这里借用Easyai的几张图和几段话:
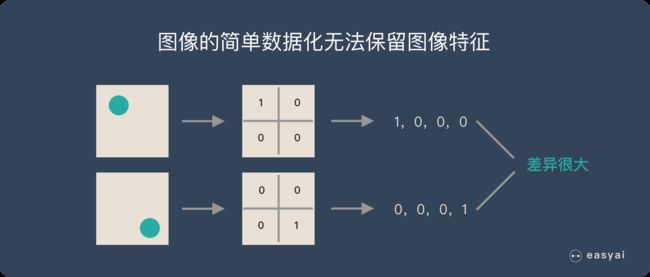
在下面的场景中,有⚪是1,否则就是0,⚪的位置不同,产生的数据也就不同,但是从视觉的角度上面来说,两张图的内容是差不多的,只在于⚪的位置的不同罢了。
而 CNN 解决了这个问题,他用类似视觉的方式保留了图像的特征,当图像做翻转,旋转或者变换位置时,它也能有效的识别出来是类似的图像。
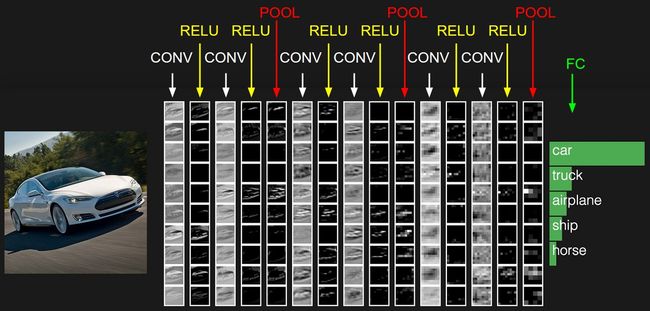
下面是一张来自cs231n中一张识别汽车的图,使用的是CNN网络,里面包含了CNN网络的网络层:
在上图中的CNN网络中,网络层有一下类型:
- CONV:卷积层,进行卷积计算然后求和。
- Relu:激励层,激励函数为Relu
- POOL:池化层
- FC:全连接层
可以很明显的看到,CNN网络与DNN网络有相似,也有不同。在CNN网络中,使用了卷积层和池化层,最后才使用全连接层,而卷积层就是CNN的核心。但是在DNN网络中全部都是全连接层。
下面将对这几层进行介绍,其中参考了YouTube上How Convolutional Neural Networks work这个视频。该视频有条件的建议去看一看,讲的还是蛮形象生动的。
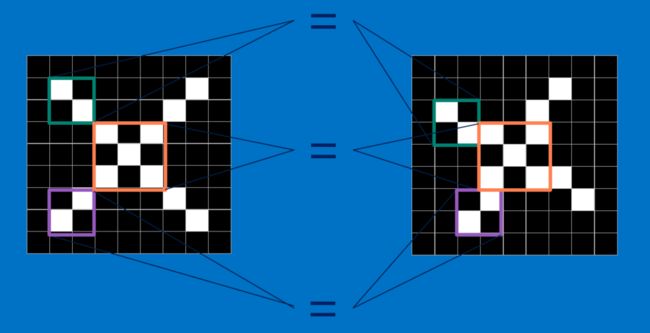
我们以识别一张照片是X还是O作为我们的识别目的:
我们如何识别一张新的图片是X还是O,肯定是拿该照片与已有的标准X和O照片进行对比,哪一个相似度高,则就认为新的照片是属于哪一个类别。对比对于人类来说很简单,但是,对于计算机来说,应该怎么对比呢?
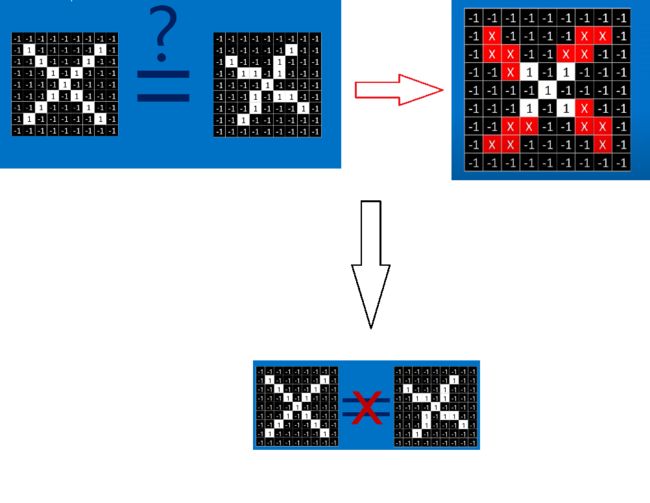
计算机可以进行遍历图片的每一个像素点的像素值,然后与标准图片的像素值进行比较,但是毋庸置疑,这样肯定是不行的,比如说在下图中计算机就认为只有中间的是一样的,其它四个角都不同,因此可能会得出这张图片不是X这个结论。
但是我们肯定是希望不管在平移,旋转,还是变形的情况下,CNN模型都可以识别出来。
so,我们将比较范围由像素点扩大到某一个范围,在CNN模型中,会比较两张图片的的各个局部,这些局部称之为特征(features)。
每一个feature都是一张小图,也就是更小的二维矩阵。这些特征会捕捉图片中的共同要素。以X图片为例,它最重要的特征就是对角线和中间的交叉。也就是说,任何叉叉的线条或中心点应该都会符合这些特征。
那么如何判断一张图片中是否有相符合的特征,然后符合的特征有多少个,这里我们使用数学的方法卷积(convolution)进行操作,这个也就是CNN名字的由来。
卷积层(Convolution Layer)
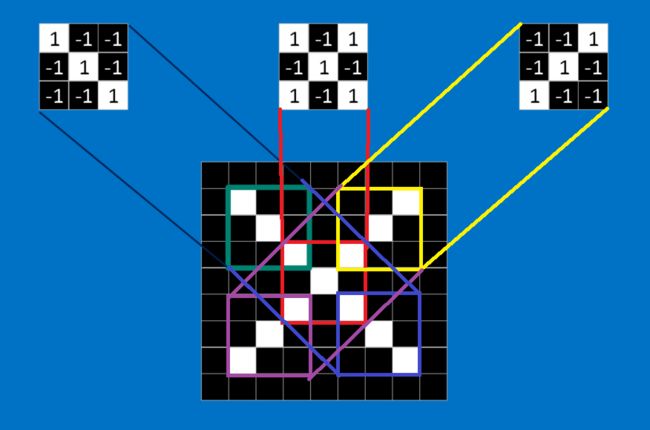
下面我还是将以识别X作为例子来讲解一下如何进行进行卷积。卷积的目的是为了计算特征与图片局部的相符程度。
计算的步骤如下:
如果我们将这个\(3 \times 3\)的特征矩阵沿着该图片以stide = 1(也就是每次滑动一格),可以得到一个\(7 \times 7\)的矩阵,最终得到的结果如下图所示:
很容易理解,卷积之后的结果越接近1,则相当与对应位置与特征feature越接近。分别与三个特征进行卷积的结果如下所示,得到了feature map:
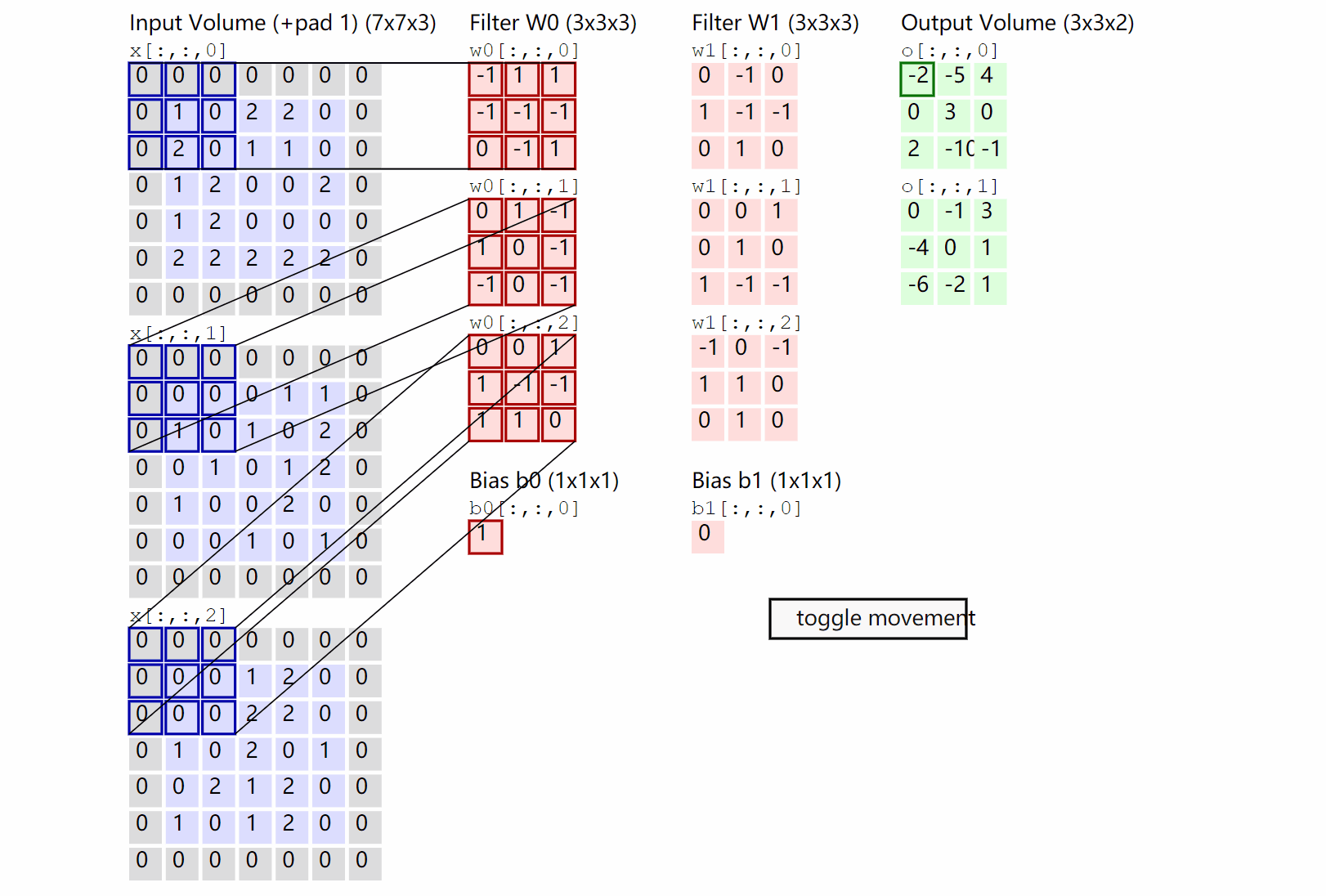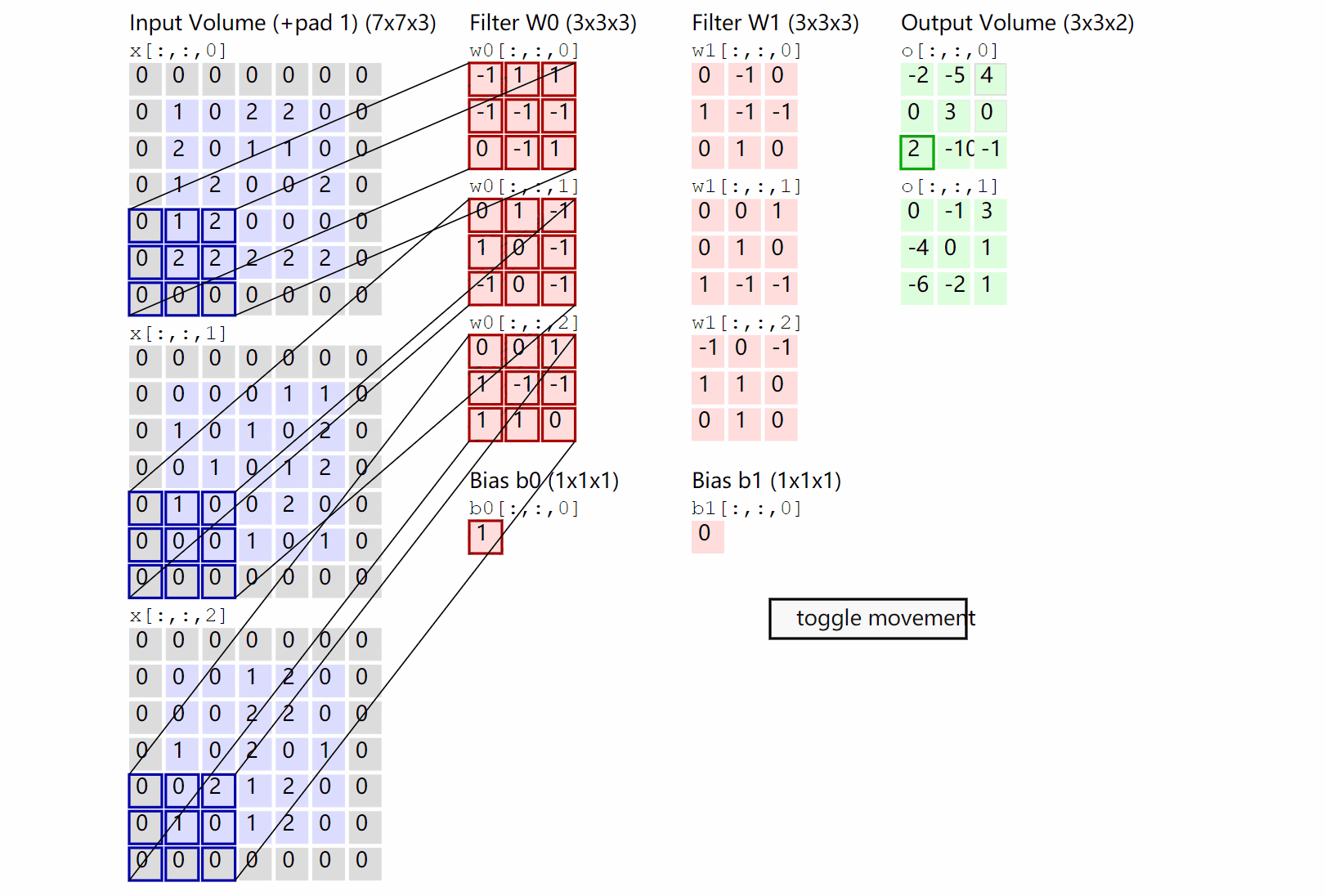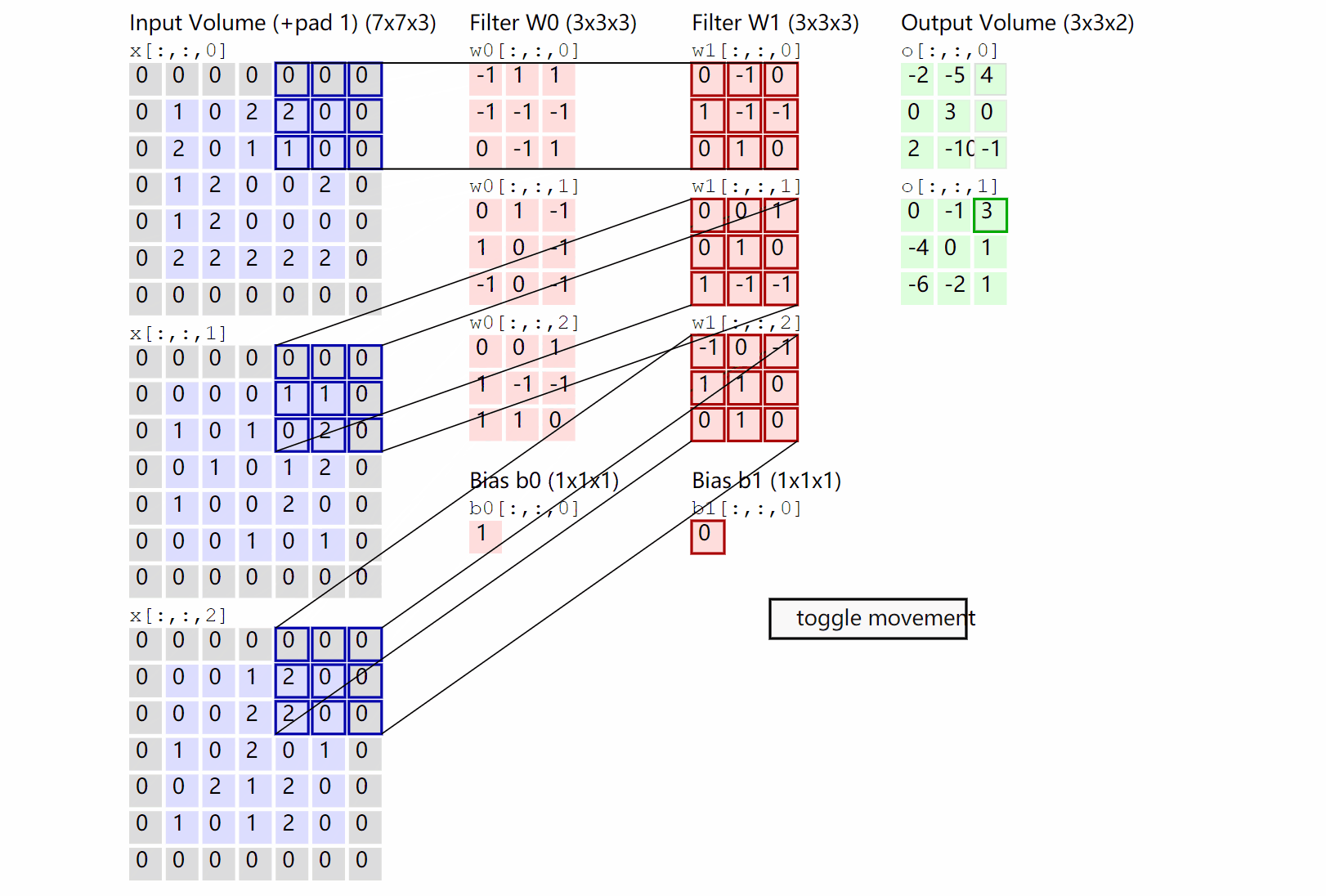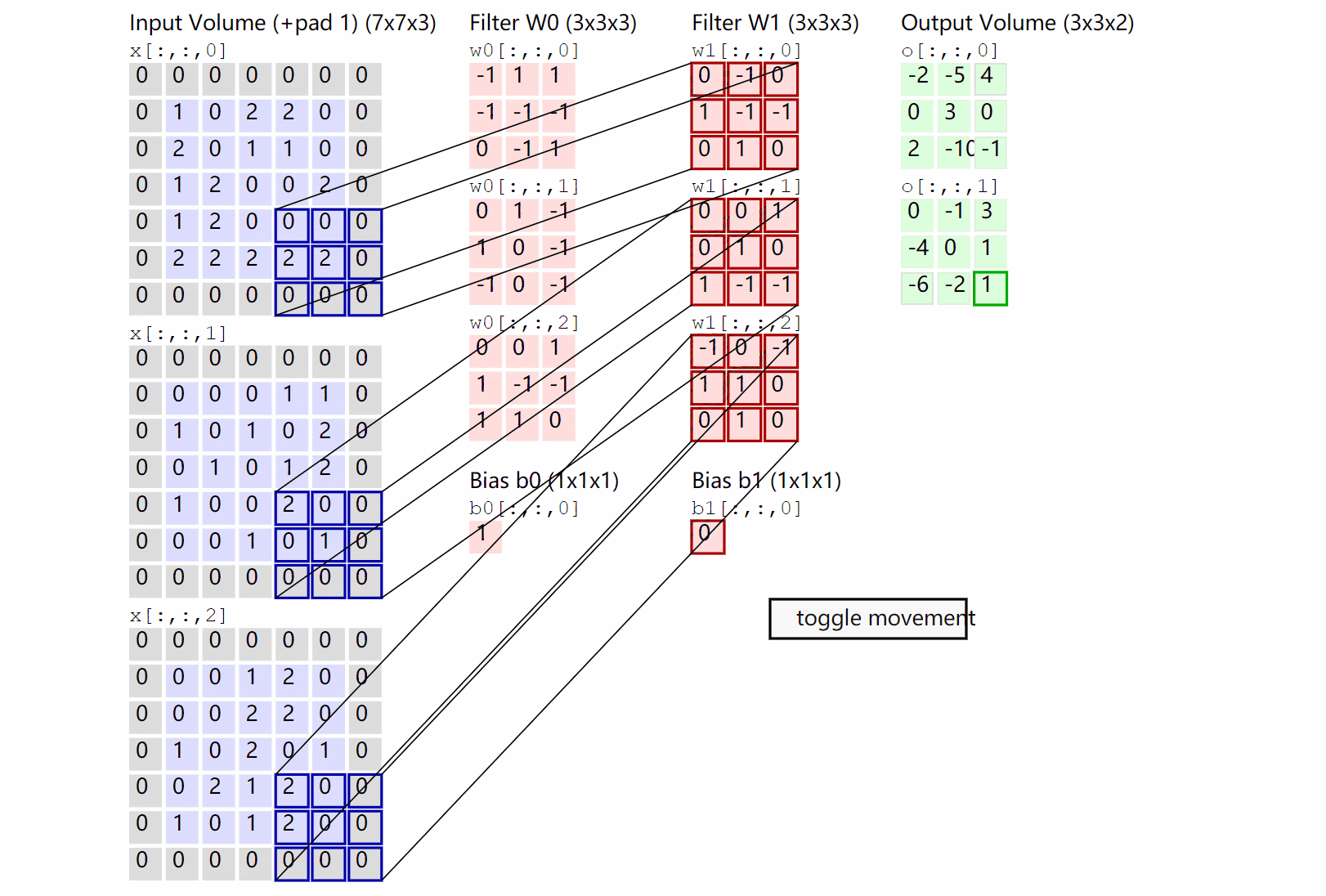
这里是一张来自cs231n的一张卷积示意图:
不过这里与上面不同的是,它并没有取平均值,同时加上了一个偏置\(b\),同时最后的结果是三个的的卷积的和。并且加上了一个padding(也就是外面那一层灰色取0的地方)
设输入的为\(W_1 \times H_1 \times D_1\),卷积核的大小是\(F \times F\),卷积核的数量是\(K\),padding的大小是\(P\),stride步为\(S\),输出的矩阵的大小是\(W_2 \times H_2 \times D_2\),则:
Relu激励层
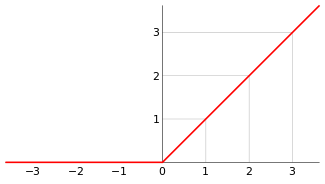
整流线性单位函数(Rectified Linear Unit, ReLU),又称修正线性单元, 是一种人工神经网络中常用的激励函数(activation function),通常指代以斜坡函数及其变种为代表的非线性函数。数学表达式为:
Relu激励层的工作流程如下所示:
将卷积层的输出通过激励层后的结果如下:
这一层还是蛮简单的,可能大家会发现,在深度神经网络中,sigmoid激活函数就很少使用了,这是因为sigmoid函数太小了,在多层神经网络下会出现”梯度消失“现象。
池化(Pooling)
池化层就更加的简单了,池化层可以大幅度的降低数据的维度。池化层多种,下面介绍两种简单常用的:
- 平均池化(
average pooling):计算图像区域的平均值作为该区域池化后的值。 - 最大池化(
max pooling):选图像区域的最大值作为该区域池化后的值。
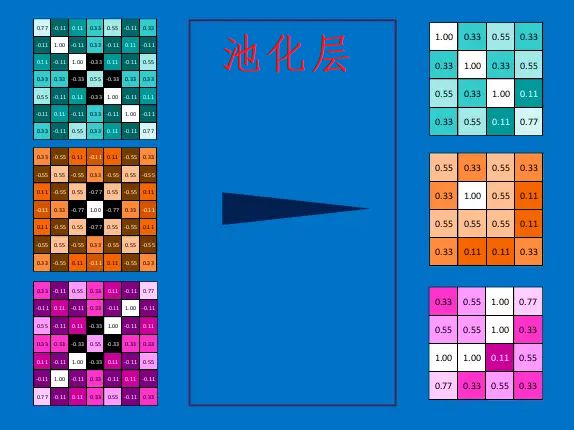
那么池化是怎么操作的呢,下面是最大池化进行操作的示意图:
池化层也就是从一定的范围(也就是池化层的大小)中选出一个(或者计算出一个)值作为这个区域范围的代表。
对所有的feature map都进行池化,最后的结果如下:
因为最大池化(max-pooling)保留了每一个小块内的最大值,所以它相当于保留了这一块最佳的匹配结果(因为值越接近1表示匹配越好)。这也就意味着它不会具体关注窗口内到底是哪一个地方匹配了,而只关注是不是有某个地方匹配上了。这也就能够看出,CNN能够发现图像中是否具有某种特征,而不用在意到底在哪里具有这种特征。这也就能够帮助解决之前提到的计算机逐一像素匹配的死板做法。
设输入的为\(W_1 \times H_1 \times D_1\),池化层的大小是\(F \times F\),stride步为\(S\),输出的矩阵的大小是\(W_2 \times H_2 \times D_2\),则:
结合卷积层、激励层、池化层
我们将前面所讲的卷积层,激励层,池化层进行结合,所得:
加大网络的层数就得到了深度神经网络:
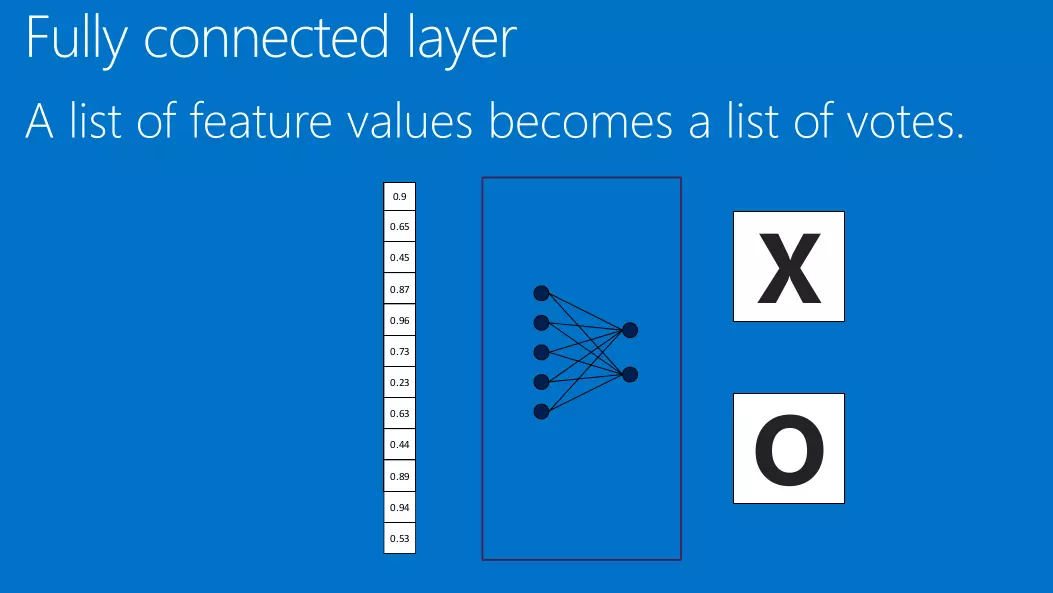
全连接层(Fully connected layers)
通过前面得卷积,池化操作,我们成功得将数据进行了降维,得到降维后的数据后,我们在将其放入全连接层中,就可以得到最终得结果。
还是以上面识别X为例子:
我们称之这一层为全连接层。
当然全连接层也可以有多个:
综上,所有得结构我们可以表达为:
同时我们可以与CS231n的图片作比较,两者是一样的。
总结
这一篇博客主要是介绍了每一层的功能,以及每一层工作的原理,但是并没有对其数学公式继续宁推导,如果想更多的了解CNN的前向和反向传播算法,可以去参考这一篇博客。
在下一篇博客中,将介绍使用CNN对cifar-10(也可能是cifar-100)进行训练预测。
参考
- Easyai
- cs231n
- 卷积神经网络的运作原理
- [透析] 卷积神经网络CNN究竟是怎样一步一步工作的?