汉明码——计算机网络——全网最通俗的讲解

   汉明码——计算机网络——全网最通俗的讲解

 

 

 

一、什么是汉明码（hamming code）

---

“汉明码”，也称作“海明码”，英文名为“hanming code”，在通信领域中，“汉明码”有广泛的应用，由理查德·卫斯里·汉明于1950年发明。“汉明码”是一种“错误纠正码”，可以用来检测并且纠正数据从发送端发往接收端中发生的错误。

汉明码的发明者理查德汉明在1940年代晚期，运用贝尔模型V（Bell Model V）电脑于贝尔实验室（Bell Labs）工作。输入端是依靠打孔卡（Punched Card），这不免会造成些读取错误。在工作日，当机器检测到错误将停止并闪灯（flash lights），使得操作员能够解决这个错误。在周末和下班期间，没有操作者的情况下，机器只会简单地转移到下一个工作。

汉明在周末工作，他对于不可靠的读卡机发生错误后，总是不得不重新启动程序变得愈来愈沮丧。在接下来的几年中，他为了解决侦错的问题，开发了功能日益强大的侦错算法。在1950年，他发表了今日所称的汉明码，并且时至今日仍在ECC memory上显示其应用价值。

 

二、先来了解什么是“冗余位”

---

“冗余位”是一种二进制位，它被用来添加到需要传输的数据信息中，以确保信息在传输过程中不会发生丢失或者改变。

对于“冗余位”究竟需要多少位这个问题，我们有一个公式可以用来计算：

其中，r指的是冗余位究竟需要多少位，而m指的是传输的数据的二进制位数。

假设传输的数据的二进制位数是7位，那么冗余位的个数就可以通过上面的公式来计算：

= 2^4 ≥ 7 + 4 + 1

因此，我们的至少需要4个二进制位作为“冗余位”。

 

三、再来了解一下“奇偶校验位”

---

一个奇偶校验位是用来添加至二进制数据中的比特位，他通过确保整个二进制数据信息中“1”的个数是奇数还是偶数，来判断数据是否在传输过程中发生的改变。因此，存在两种类型的检测方式：

一、奇校验

在奇校验检测方式中，对于需要发送的数据信息比特，检查其中1的个数。如果这串比特中1的个数是奇数，为了保证加上“冗余位“后，””整串数据中1的个数最后为奇数，可想而知，冗余位上应该设置为“0”。如果在没有添加“冗余位”之前，数据比特流中的1的个数为偶数，那么为了最后把1的个数凑成一个奇数，冗余位上应该设置为1.

二、偶校验

同理，在偶校验检测方式中，对于需要发送的数据信息比特，仍然检查其中1的个数。如果这串比特中1的个数是奇数，为了保证加上“冗余位“后，””整串数据中1的个数最后为偶数，可想而知，冗余位上应该设置为“1”。如果在没有添加“冗余位”之前，数据比特流中的1的个数为偶数，那么为了最后把1的个数凑成一个偶数，冗余位上应该设置为0.

本次我们使用“偶校验”来作为演示，即我们要保证数据二进制位加上“奇偶校验位”的整个数据中，“1”的个数应该为偶数。

假设本次需要传递的数据信息为3位二进制位，演示动画如下：（点击动图可全屏观看，效果更佳！）

 

 

 

正如动画演示的那样，我们的“奇偶校验位”就成功的添加到了需要传递的数据信息中了，本次动画中采用的是“偶校验”的方式，即1的个数最后一定要满足是1个偶数。假设在传输过程中，其中1位数字发生了改变，又会发生什么样的情况呢？我们仍然使用上面动画所描述的情况：假设在传输过程中，其中1位数据位发生了改变。（点击动图全屏观看效果更佳！）

 

此时，偶校验电路发现最后“1”的个数不是一个偶数了，说明在数据传输过程中，数据肯定发生了改变。然而，“奇偶校验法”仍然存在下面两条缺点：

一、虽然知道数据在传输过程中发生了改变，但并不知道是哪一位发生了改变，因而无法纠正错误，只能要求发送方重新发送一遍数据。

二、“奇偶校验法”只能发现1位，3位，5位。。。。。。奇数个二进制位发生改变，假设数据传输过程中有2位发生改变，则“奇偶校验法”并不能发现数据已经被更改了，仍然认为数据是无误的。如下动画演示：（点击动图全屏观看效果更佳！）

 

 

 四、汉明码的编码方式

---

汉明码对于初学者来说，可能会让人头大一些。但是，如果你认真阅读并理解了上面讲述的“奇偶校验法”的话，汉明码将会变得非常简单。我们上面讲述了“奇偶校验法”的两个缺点，其中一个是当传输过程中发生了2位或更大的偶数位改变时，奇偶校验法将会变得失效。然而，随着科学技术的飞速发展，如今在数据通信传输过程中，数据发生改变的几率是非常非常的小了，1位数据发生改变的几率更加小，因此，2位即2位以上比特位发生改变的情况我们假设其永远不可能发生。因此，我们剩下来需要解决的问题就是：假设有1位发生改变，有没有什么办法能够让我们发现是哪一位发生了改变呢？如果能找到是哪一位发生了改变，我们就能够纠正它，0变1,1变0。汉明码就很好的解决了这个问题。

首先，让我们来看一下汉明码是如何编码的吧！汉明码其实就是“奇偶校验法”的升级版，它是多个“奇偶校验法”的组合糅合在一起，但是奇偶校验位的位置不一定再是最后一位了，而是有其他的计算方法。

假设我们需要传输的数据信息是由7位二进制位组成，通过第二部分我们已经算出来了至少需要4位冗余位。因此，整个信息流有11个二进制位。其中有7位数据位和4位“奇偶校验位”。

 

此时肯定有同学会想当然了，最后的4,3,2,1位置上肯定就是4个“奇偶校验位”，其实汉明码对于“奇偶校验位”的位置有特殊的规定：

所有2的幂次位（2^0=1,2^1=2,2^2=4,2^3=8……）作为“奇偶校验位”，因此，第1位，第2位，第4位，第8位为奇偶校验位，其他的7位为数据位。

此时，肯定又有同学会犯迷糊了，“奇偶校验位”如果这样安排的话，那哪个奇偶校验位又“管着”哪一组数据呢？

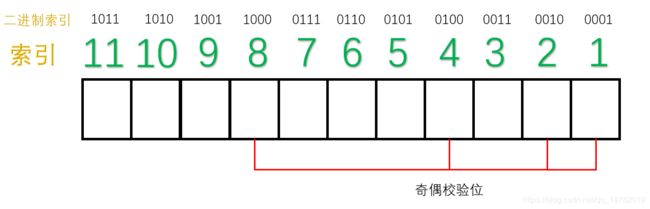
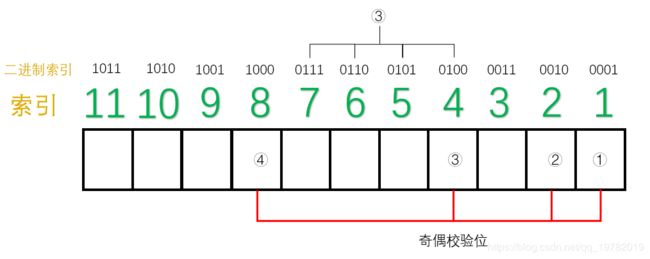
此时，就要讲到汉明码的核心编码方法了，我们把索引的二进制形式表示出来，如下图所示：

 

我们接下来可以对二进制索引通过一个这样的方法对其分类：

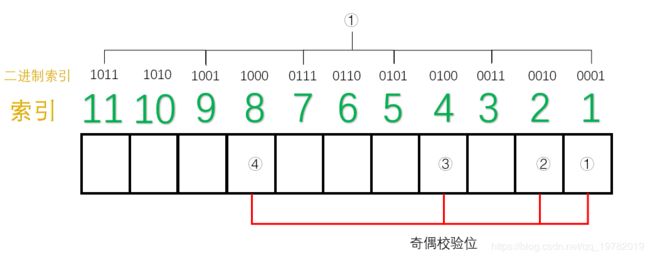
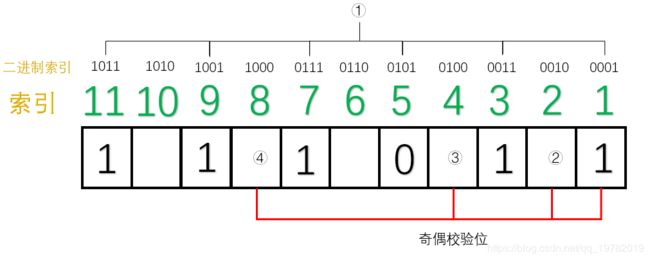
从右往左（低位往高位）数，第一位是“1”的索引有：1011，1001,0111,0101,0011,0001

分别对应的10进制索引为：11,9，7,5,3,1，那么，这几位上面的数据位和1号“奇偶校验位”构成了一组。

如下图所示：

 

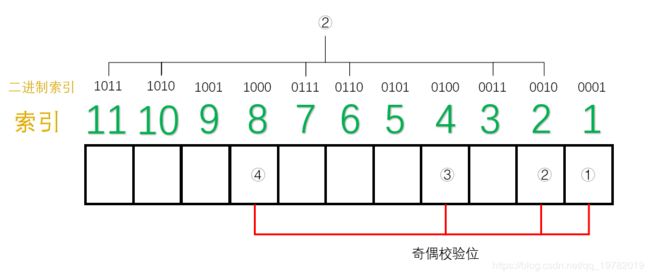
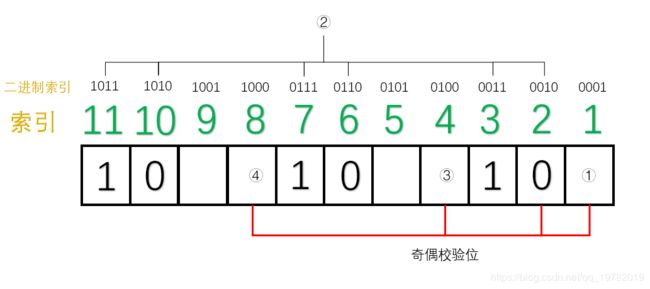
同理：从右往左（低位往高位）数，第二位是“1”的索引有：1011，1010,0111,0110,0011,0010

分别对应10进制索引为：11,10,7,6,3,2，那么，这几位上面的数据位和2号“奇偶校验位”构成了一组。

如下图所示：

 

同理 ，3号奇偶校验位“管理”的数据位分别如下：

4号奇偶校验位“管理”的数据位分别如下：

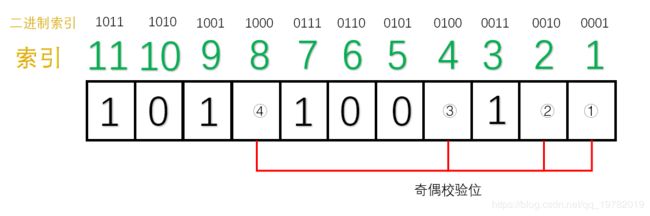
这样，分组我们就已经确立好了，接下来需要开始填充数据位，假设我们需要传输的7位数据位：1011001

如下图所示：

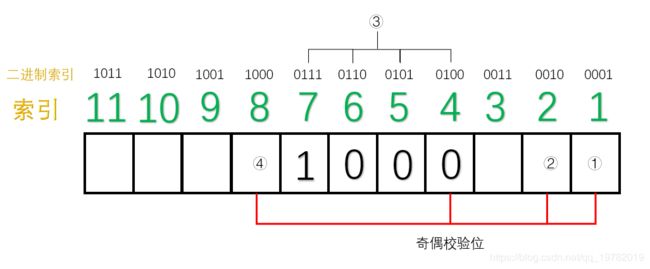
接下来，我们就需要分别填充每一组的“奇偶校验位”了。（采用奇校验）

对于第一组来说（1,3,5,7,9,11位为一组）：1的个数为4个，偶数个，因此①号应该为1。这样1的个数最后才能保证为奇数。

同理，对于第二组来说（2,3,6,7，10,11位1组）：1的个数为3个，已经是奇数了，因此②号应该是0。

对于第三组来说（4,5,6,7位一组），1的个数为1个，因此，③号应该是0。

 

对于第4组来说（8,9,10,11为一组），1的个数为2个，因此，④应该为1。

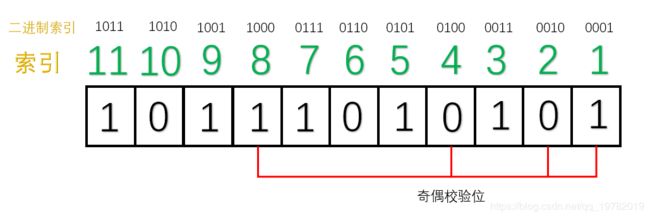
最后，总的汉明码就构造完毕了，如下所示：

 

汉明码的“纠错”和“改正” 

---

上面，我们已经完成了“汉明码”的编码，那么，汉明码又是如何发现错误以及改正错误的呢？

假设，第“5”号位上的“0”在传输过程中变成了“1”，接收方收到的数据则为：10111010101。

 

汉明码通过检查每一小组的“奇校验”，来确定是否发生了错误。

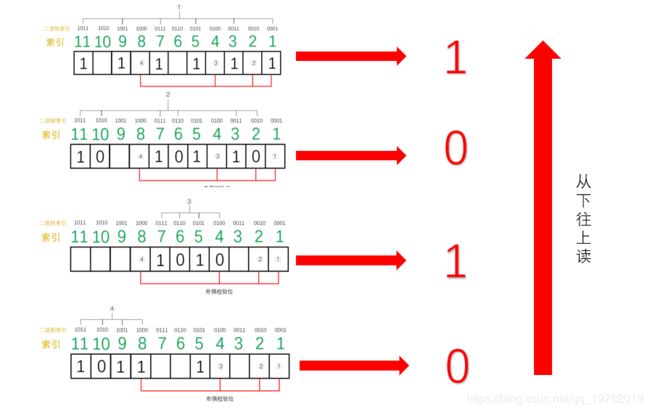
首先第一组（1,3,5,7,9,11位）：1的个数为6位，不再是奇数个了，因此，我们可以断定，这一组中肯定有某个数据发生了错误，但不能确定是哪一位上发生了错误。为了达到“奇校验”，我们必须补1个1来达到奇数个1。

接下来，我们检查第二组（2,3,6,7，10,11） ，1的个数为3位，仍然满足“奇校验”，因此我们也可以断定这一组中没有任何一位数据发生了改变。所以，我们只需要补0。

我们继续检查第三组（4,5,6,7），1的个数为2个，不在满足“奇校验”，因此，我们可以断定，这一组中也有数据发生改变。为了达到“奇校验”，我们必须补1个1来达到奇数个1。

我们检查第4组（8,9,10,11位），1的个数为3位，满足“奇校验”，因此没有发生改变。所以我们只需要补0。

如下图所示：

 我们发现，最后得出来的二进制数是：0101，我们会神奇地发现，0101就是10进制5的二进制表现，因此，我们可以准确的知道，5号位上发生了数据的改变，我们只要对5号位进行置反操作即可。最后，接收方就可以修改成为正确的数据啦。

虽然我们觉得汉明码无论是“编码”还是“纠错”都有点小小的复杂，但是通过特定的电子技术可以设计出很快的电子元件来专门进行这些操作。

 

参考资料

---

【1】Computer Network | Hamming Code https://www.geeksforgeeks.org/computer-network-hamming-code/

作者：Harshita Pandey 翻译：刘扬俊

【2】维基百科——汉明码

 

博客文章版权声明

---