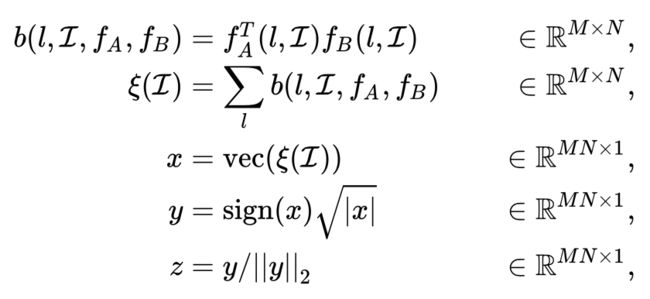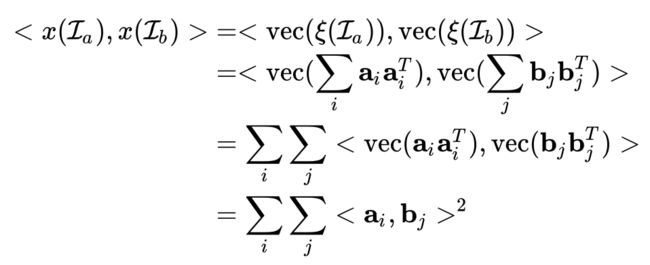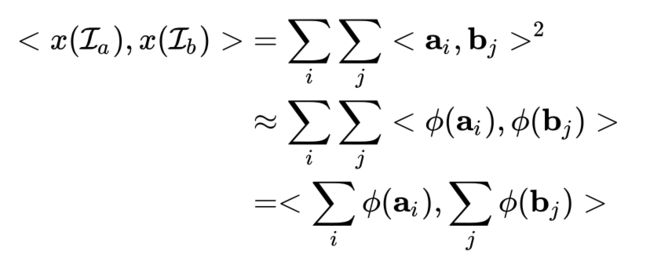【笔记】双线性池化(Bilinear Pooling)详解、改进及应用
点击上方,选择星标或置顶,每天给你送干货![]() !
!
阅读大概需要16分钟
跟随小博主,每天进步一丢丢
来自 | 知乎
作者丨林小北
来源丨https://zhuanlan.zhihu.com/p/62532887
本文仅供交流,如有侵权,请联系删除。
最近看了一系列bilinear pooling相关的文章,感觉有些文章写得比较抽象。费了不少功夫总算理顺了这些文章的关系,这里简单写个笔记记录一下~
一、简介
bilinear pooling在2015年于《Bilinear CNN Models for Fine-grained Visual Recognition》被提出来用于fine-grained分类后,又引发了一波关注。bilinear pooling主要用于特征融合,对于从同一个样本提取出来的特征x和特征y,通过bilinear pooling得到两个特征融合后的向量,进而用来分类。
如果特征x和特征y来自两个特征提取器,则被称为多模双线性池化(MBP,Multimodal Bilinear Pooling);如果特征x=特征y,则被称为同源双线性池化(HBP,Homogeneous Bilinear Pooling)或者二阶池化(Second-order Pooling)。此外,有些文章也把bilinear model称为bilinear pooling(这么做是有原因的,下文会分析)。
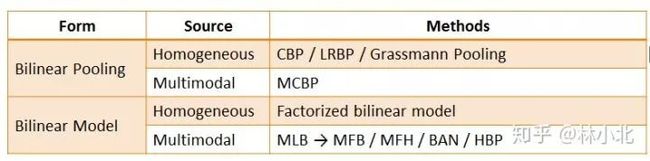
原始的Bilinear Pooling存在融合后的特征维数过高的问题,融合后的特征维数=特征x和特征y的维数之积。原作者尝试了PCA降维,但效果并不理想。基于降低bilinear pooling特征维数的思想,近年来的改进方案参见下表:
本文将包括以下内容:
对bilinear pooling进行详细介绍,便于读者理解原文;
建立bilinear pooling到bilinear model的联系,便于读者理解以MLB为核心的bilinear model相关文章。
快速介绍对bilinear pooling的各种改进形式。
二、bilinear pooling详解
这里参考《Bilinear CNN Models for Fine-grained Visual Recognition》,CVPR 2015一文,给出bilinear pooling的详细定义。
对于图像 在位置 的两个特征 和 , 进行如下操作:
直观上理解,所谓bilinear pooling,就是先把在同一位置上的两个特征双线性融合(相乘)后,得到矩阵 ,对所有位置的 进行sum pooling(也可以是max pooling,但一般采用sum pooling以方便进行矩阵运算)得到矩阵 ,最后把矩阵 张成一个向量,记为bilinear vector 。对 进行矩归一化操作和L2归一化操作后,就得到融合后的特征 。之后,就可以把特征 用于fine-grained分类了,如下图所示:
对于我们熟悉的图像特征, ,而 和 分为别特征的通道数,把两个特征分别写成向量
和 ,
有
记 ,
,
即可用矩阵操作来表示生成 ,
即
作者使用bilinear pooling对两种特征提取器进行融合,再用于fine-grained分类,取得不错的效果。bilinear pooling的形式简单,便于梯度反向传播,进而实现端到端的训练。

三、Second-order Pooling
Second-order Pooling最早出自ECCV2012的文章《Semantic segmentation with second-order pooling》,原文对Second-order Pooling的定义如下:

由于Second-order Pooling用到了特征x的二阶信息,所以在一些任务下能比一阶信息表现更为优秀。
对比bilinear pooling的定义,不难发现,当 的时候,二者是等价的。也就是说,二阶池化(Second-order Pooling)=同源双线性池化(HBP,Homogeneous Bilinear Pooling)。
下面介绍bilinear pooling的各种改进。
四、CBP: Compact Bilinear Pooling
CBP出自CVPR 2016《Compact bilinear pooling》一文,作者观察到在分类问题中,提取的特征常常采用SVM或者logistic regression,而这两种形式都可以被看作是线性核机器(linear kernel machines),具有如下的形式:
注意到
如果我们能够找到满足 的低维投影函数 ,那么有
也就是说,当 时,有 。基于这个思想,作者提出了采用了两种方法 Random Maclaurin (RM)和Tensor Sketch (TS)对bilinear pooling进行降维。具体细节如下:
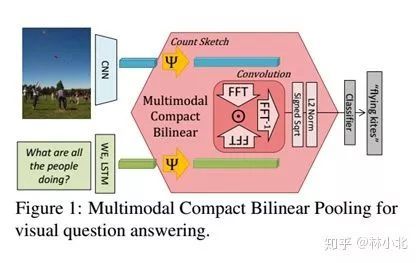
五、MCBP: Multimodal Compact Bilinear Pooling
《Multimodal compact bilinear pooling for visual question answering and visual grounding》是EMNLP2016的文章。本文在CBP的基础上提出了MCBP,并将其应用于看图答题(VQA,visual question answering)领域。
注意到CBP是针对HBP进行改进的,对CBP的TS算法稍加改动,使其适用于融合不同模态的特征,即可得到MCBP,如下图所示。
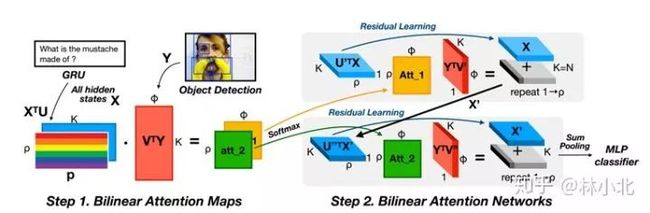
在得到MCBP模块后,作者提出用于VQA的网络结构如下:
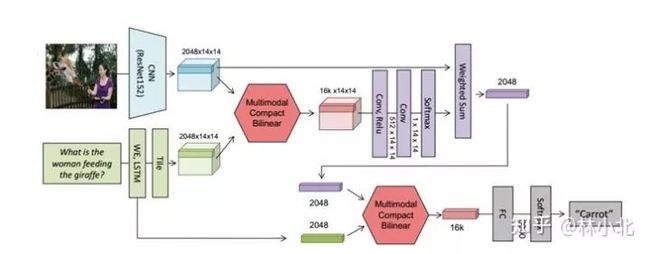
这个结构相当容易理解,就是一共用到了两次MCBP模块,第一个MCBP融合了文本和图像的特征进而用来提取图像的attention,第二个MCBP则把图像的attention特征与文本特征再一次融合,最终结果送入softmax分类器得到答案。
六、LRBP:Low-rank Bilinear Pooling
LRBP出自CVPR2017的文章《Low-rank bilinear pooling for fine-grained classification》,与CBP一样,都是假定采用的分类器是SVM来对HBP进行简化。
考虑SVM问题
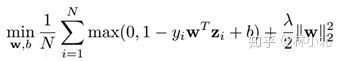
的最优解w*,以及问题
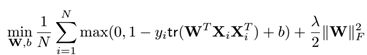
的最优解W*,作者证明了
并且W*是实对称矩阵。实对称矩阵的一大优点是可以进行特征值分解,即

如果用两个低秩矩阵U+和U_去近W*,则问题转换为:
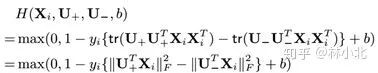
这样就避免了原始bilinear pooling里面 的计算,降低了计算量。
七、Grassmann Pooling
Grassmann Pooling出自ECCV 2018的文章《Grassmann Pooling as Compact Homogeneous Bilinear Pooling for Fine-Grained Visual Classification》,也是针对HBP的改进。
考虑形式为
的bilinear pooling,有引理如下:
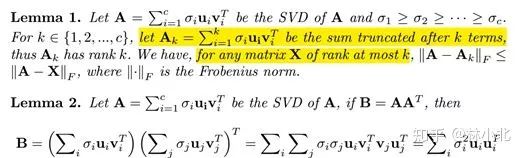
也就是说,对矩阵 进行SVD分解,前k个左奇异向量组成的矩阵 是对矩阵 的低秩最优逼近。
基于这个引理,作者提出了Grassmann pooling如下:

显然,Grassmann pooling也能够简化bilinear pooling计算量。
上面提到的三种改进形式CBP、LRBP、Grassmann Pooling都是针对HBP的改进。MCBP直接对CBP改动用于多模态特征的融合,但是考虑到CBP的出发点是核函数,MCBP的改动其实有点站不住脚的。对于MBP的改进工作,主要是以MLB为基础。MLB的核心是利用Hadamard积来简化bilinear model的操作。在介绍MLB之前,先介绍一篇承上启下的工作,把bilinear pooling和billinear model建立联系。
八、从bilinear pooling到billinear model
《Factorized bilinear models for image recognition》是ICCV2017的文章,虽然本文也是针对HBP的研究,但成功地把bilinear model与bilinear pooling联系起来。而后面的工作MLB正是从bilinear model的角度出发去改进MBP。
首先介绍bilinear model,对于特征向量x和特征向量y,bilinear model是指形如

的操作。
忽视bilinear pooling的归一化操作,记HBP的特征为 ,
在分类任务中,我们常常会把提取的特征送入全连接层再送入softmax层。作者发现,这个操作与bilinear model是等价的,即

其中 是全连接层的参数矩阵,而 是与其相对应的一个矩阵。既然 是需要通过学习得到的,那不如直接写成bilinear model的形式,对 进行学习。
也就是说,bilinear pooling与bilinear model是等价的。更令人欣喜的是,这个结论对于MBP也是适用的,所以后面MLB直接针对bilinear model进行改进。
基于这个发现,作者提出了Factorized bilinear model,把特征的一阶信息和二阶信息都利用起来,进而更好的fine-grained分类,其形式如下:
这里利用低秩矩阵 来替代 ,简化了计算量。
九、MLB:Multimodal Low-rank Bilinear Pooling
有了上篇工作的介绍,理解MLB就非常容易了,MLB出自ICLR2017的文章《 Hadamard product for low-rank bilinear pooling》。文章核心是用Hadamard积(就是按元素乘)来实现bilinear model,把
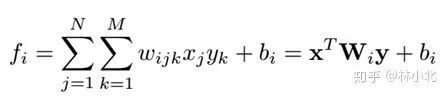
写成了
这样的好处是,利用低秩矩阵 及 来近似 ,并且简化了操作。
当希望bilinear model的输出是向量的时候,只需扩大矩阵 及 ,并采用矩阵 控制输出的长度即可,如下所示:
本文的写作相当严谨,各个矩阵的尺寸大小均有注明,有兴趣的读者自行翻阅。
十、MFB:Multi-modal factorized bilinear pooling
MFB出自ICCV2017《Multi-modal factorized bilinear pooling with co-attention learning for visual question answering》。本文的思路与MLB十分相似,不同点在于当希望bilinear model的输出是向量的时候,本文直接把U和V变成了三维张量,再通过sum pooling来进行通道融合得到最后的输出。
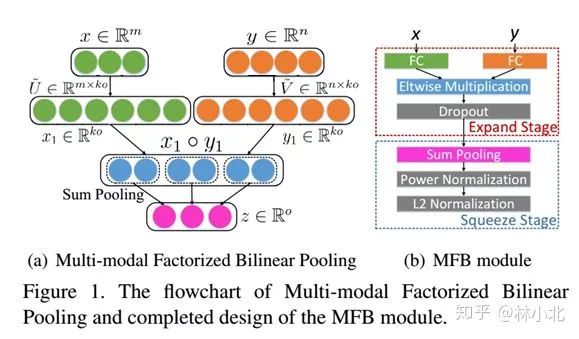
在MFB的基础上,作者于《Beyond bilinear: Generalized multimodal factorized high-order pooling for visual question answering》一文中提出了MFH(Multi-modal factorized high-order pooling )。把MFB操作分为两个阶段Expand Stage和Squeeze Stage,MFH就是把MFB堆叠起来以得到高阶信息,如下图所示

作者成功地把MFB/MFH应用于VQA,提出的网络结构如下:

这个结构与前文提到的《Multimodal compact bilinear pooling for visual question answering and visual grounding》相当类似,都是利用融合后的特征提取图像的attention特征,再进而第二次融合进而用来分类。不同之处在于,作者模拟了人类“审题”的思维模式,先建立了文本的attention特征,再去考虑与图像的特征融合。
前面介绍的工作,都是针对bilinear pooling的计算量过大而进行的改进。作为融合特征的有效方法,bilinear pooling在fine-grained分类和VQA都有不错的发挥。这里再简要介绍bilinear pooling的几篇应用。
十一、应用于VQA领域的《Bilinear attention networks》
本文是MLB的续作,发表于NIPS2018。本文借助bilinear model的思想提出了bilinear attention的思想。常规的attention map是对单个特征的attention,output=feature * attention map,而本文提出的bilinear attention map则对两个特征的attention, output=feature1 * bilinear attention map * feature2,表达式如下:
这个表达式与MLB十分相似,可以说是一脉相承。
本文提出的网络结构如下所示,左图通过MLB把图像特征和文本特征融合,进而得到bilinear attention map,右图则是把bilinear attention map用于进行图像特征和文本特征的attention融合。该网络较为复杂,有兴趣的读者自行翻阅原文。
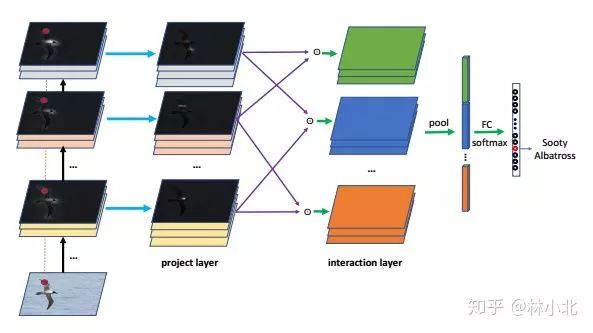
应用于分类领域的《Hierarchical Bilinear Pooling for Fine-Grained Visual Recognition》
本文出自ECCV2018,核心思想是把不同层的特征通过bilinear pooling两两融合,最后concate后进行分类。
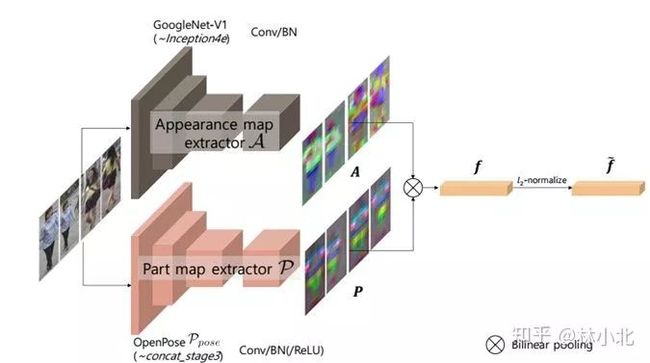
应用于ReID领域的《Part-Aligned Bilinear Representations for Person Re-Identification》
本文出自ECCV2018,核心是把行人的全局特征与局部特征(通过openpose预训练得到)通过bilinear pooling融合,再进行检索。
应用于三维物品识别领域的《Multi-View Harmonized Bilinear Network for 3D Object Recognition》
本文出自CVPR 2018,核心是利用HBP提取多视角特征。

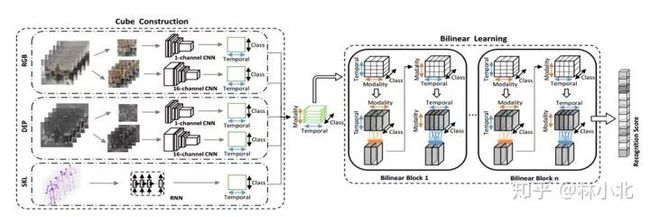
应用于动作识别领域的《Deep Bilinear Learning for RGB-D Action Recognition》
本文出自ECCV 2018,基于bilinear model提出了bilinear block,来更好地融合多模态信息。
方便交流学习,备注:昵称-学校(公司)-方向,进入DL&NLP交流群。
方向有很多:机器学习、深度学习,python,情感分析、意见挖掘、句法分析、机器翻译、人机对话、知识图谱、语音识别等。记得备注呦推荐阅读:【ACL 2019】腾讯AI Lab解读三大前沿方向及20篇入选论文【一分钟论文】IJCAI2019 | Self-attentive Biaffine Dependency Parsing
【一分钟论文】 NAACL2019-使用感知句法词表示的句法增强神经机器翻译
【一分钟论文】Semi-supervised Sequence Learning半监督序列学习
【一分钟论文】Deep Biaffine Attention for Neural Dependency Parsing
详解Transition-based Dependency parser基于转移的依存句法解析器经验 | 初入NLP领域的一些小建议
学术 | 如何写一篇合格的NLP论文
干货 | 那些高产的学者都是怎样工作的?
一个简单有效的联合模型近年来NLP在法律领域的相关研究工作让更多的人知道你“在看”