校园导航系统（数据结构C语言邻接矩阵为存储结构和迪杰斯特拉算法求最短距离）

校园导航系统（数据结构C语言实现）

开发工具：Dev-C++；
（1）设计任务
掌握图的结构特点及应用，运用所学知识解决现实问题。给出校园各主要建筑的名称信息及有线路联通的建筑之间的距离，利用校园导航系统计算出输入的起点到终点之间的最近距离及线路。
（2）设计要求
①输入各建筑信息及线路信息，构建图。本项目数据结构为有向网，采用邻接矩阵为存储结构。
②计算给定起点到终点之间最近距离的进行线路。参照迪杰斯特拉算法计算给定两点之间的最短路径。
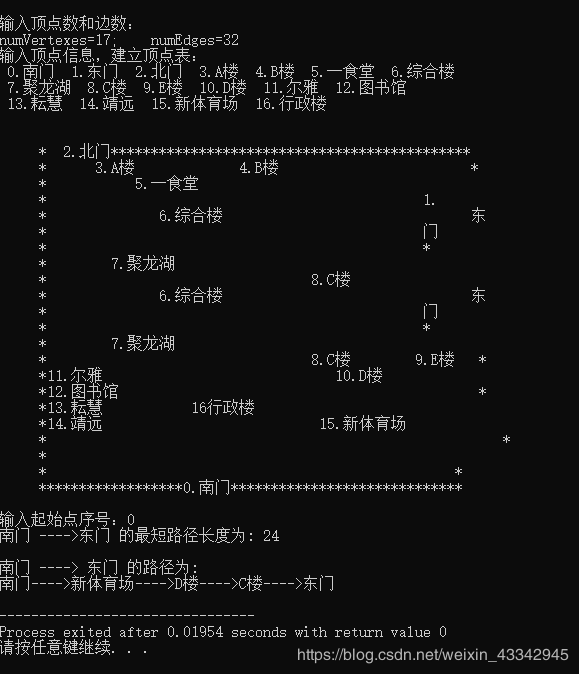
③根据输入起点和终点，输出线路及总距离。

说明：
采用邻接矩阵为存储结构和迪杰斯特拉算法求最短距离实现功能；
代码已经为输入值赋值，可以自行修改相关代码；
创建图的函数也已经为图的各个顶点和权值赋值，可以自己修改；
主函数中有输出全部结果的相关代码；

#include "stdio.h"    
#include"string.h"
#define MAXVEX 20 		  //最大顶点数     
#define INFINITY 65535    //65535代表 ∞     
#define TRUE 1    
#define FALSE 0    
#define OK 1    
#define ERROR 0

   
typedef int Status;	    			/* Status是函数的类型,其值是函数结果状态代码，如OK等 */ 
typedef char    VertexType;    //顶点类型 
typedef int EdgeType;            //边的权值类型 
typedef int    Patharc[MAXVEX];                /* 用于存储最短路径下标的数组 */ 
typedef int    ShortPathTable[MAXVEX];  /* 用于存储到各点最短路径的权值和 */
 
typedef struct 
{ 	
	 VertexType vexs[MAXVEX][MAXVEX];     //顶点表 	
	 EdgeType    arc[MAXVEX][MAXVEX];     //邻接矩阵 	
	 int numVertexes, numEdges;                   //图中当前顶点数和边数 
} MGraph;
   
void CreateMGraph(MGraph *G);//邻接矩阵创建网图 
void map();//地图 
void    ShortestPath_Dijkstra(MGraph G, int v0, Patharc *P, ShortPathTable    *D); /*---迪杰斯特拉算法---*/
       
int main() 
{ 	
    int i,j,v0,v1,a[MAXVEX]; 	MGraph G; 	Patharc P;
	ShortPathTable D; /* 求某点到其余各点的最短路径 */
   
   
    printf("\n"); 	
    CreateMGraph(&G); 	
    printf("\n");
	   
    map();//校园地图
   
   	v0=0; 	
   	printf("\n输入起始点序号：%d",v0); 	//printf("\n输入起始点序号:");
   	//scanf("%d",&v0);
   
   	ShortestPath_Dijkstra(G, v0, &P, &D);
   
   	//v0-->v1的最短距离 	v1=5; 	printf("\n输入终点点序号：%d\n",v1);
   	//printf("\n输入终点点序号:"); 	//scanf("%d",&v1);
   
   
   	printf("\n%s ---->%s 的最短路径长度为: %d \n",G.vexs[v0],G.vexs[v1],D[v1]);
   
   	j=v1; 	
   	for(i=0; P[j]!=-1; i++)  	{ 		a[i]=P[j]; 		j=P[j]; 	}
   
   	printf("\n%s ----> %s 的路径为:  \n",G.vexs[v0],G.vexs[v1]); 	
   	j=v1;
   	printf("%s---->",G.vexs[v0]); 	
   	for(i--; i>=0; i-- ) 
   		printf("%s---->",G.vexs[a[i]]);
   
   
   	printf("%s",G.vexs[v1]); 	printf("\n");
   
   
        	/* 	
		   	//算法的全部可能结果  	
		   	for(int k=0;k%s的最短路径长度: %d ",G.vexs[v0],G.vexs[i],D[i]);
		   		  printf("%s---->%s的路径: ",G.vexs[v0],G.vexs[i]);
		   		  j=i;
		   		  printf("%s",G.vexs[i]);
		   		  while(P[j]!=-1) 
		   		     { 			printf("<----%s ",G.vexs[P[j]]); 			
		   		  				j=P[j];
		   		      }
		   		   
		   		  printf("<----%s \n",G.vexs[v0]);
		   		  printf("\n");
		   	    } 	 	
		   	 } 	
   	   */
   
   	return 0; 
   	}
   
   
   
   
   
       /* 构造图 */ 
 void CreateMGraph(MGraph *G) 
 { 	
	  int i,j,k,w;
	   
	   	printf("输入顶点数和边数：\n");
	   	//scanf("%d%d",&G->numVertexes,&G->numEdges);
	    //输入顶点数和边数
	   	G->numEdges=32; 	G->numVertexes=17; 	
	   	printf("numVertexes=%d;    numEdges=%d",G->numVertexes,G->numEdges);
	   
	   	printf("\n输入顶点信息，建立顶点表：\n");
	   	
	   	/*
	   	for(i=0;inumVertexes;i++)//读入顶点信息，建立顶点表
	   		scanf("%s",&G->vexs[i]);
	   	*/
	   
	   	strcpy(G->vexs[0],"南门"); 	strcpy(G->vexs[1],"东门");
	   	strcpy(G->vexs[2],"北门"); 	strcpy(G->vexs[3],"A楼");
	   	strcpy(G->vexs[4],"B楼"); 	strcpy(G->vexs[5],"一食堂");
	   	strcpy(G->vexs[6],"综合楼"); 	strcpy(G->vexs[7],"聚龙湖");
	   	strcpy(G->vexs[8],"C楼"); 	strcpy(G->vexs[9],"E楼");
	   	strcpy(G->vexs[10],"D楼"); 	strcpy(G->vexs[11],"尔雅");
	   	strcpy(G->vexs[12],"图书馆"); 	strcpy(G->vexs[13],"耘慧");
	   	strcpy(G->vexs[14],"靖远"); 	strcpy(G->vexs[15],"新体育场");
	   	strcpy(G->vexs[16],"行政楼");
	   
	   	for(j=0; jnumVertexes; j++) 
	   	{ 		
	   		printf(" %d.%s ",j,G->vexs[j]);
	   		if(j!=0&&j%6==0) printf(" \n"); 	
	   	} 	
	   		printf(" \n\n");
	   
	   
	   	for(i=0; inumVertexes; i++) //邻接矩阵初始化 		
	   	for(j=0;    jnumVertexes; j++) 			
	   			G->arc[i][j]=INFINITY; 	
	   	
	   	/*
	   	for(k=0;knumEdges;k++) 	
	   	{ 		
	   			printf("输入边（vi，vj）上    的下标i，下标j和权w；\n"); 		
	   			scanf("%d%d%d",&i,&j,&w);//输入边和权
	   
	   		G->arc[i][j]=w; 		//printf("i=%d,j=%d,G->arc[i][j]=%d",i,j,w);
	   		G->arc[j][i]=G->arc[i][j];//无向图矩阵对称 	 
	   	} 	 
	   	*/
	   
	   	G->arc[0][14]=G->arc[14][0]=10; 	G->arc[0][16]=G->arc[16][0]=4;
	   	G->arc[0][15]=G->arc[15][0]=13;
	   
	   	G->arc[1][8]=G->arc[8][1]=8; 	G->arc[1][9]=G->arc[9][1]=7;
	   
	   	G->arc[2][3]=G->arc[3][2]=5; 	G->arc[2][11]=G->arc[11][2]=20;
	   
	   	G->arc[3][4]=G->arc[4][3]=2; 	G->arc[3][5]=G->arc[5][3]=3;
	   
	   	G->arc[4][5]=G->arc[5][4]=2; 	G->arc[4][6]=G->arc[6][4]=3;
	   
	   	G->arc[5][6]=G->arc[6][5]=1; 	G->arc[5][11]=G->arc[11][5]=10;
	   
	   	G->arc[6][11]=G->arc[11][6]=9; 	G->arc[6][7]=G->arc[7][6]=3;
	   	G->arc[6][8]=G->arc[8][6]=4;
	   
	   	G->arc[7][8]=G->arc[8][7]=5; 	G->arc[7][11]=G->arc[11][7]=4;
	   	G->arc[7][15]=G->arc[15][7]=7; 	G->arc[7][12]=G->arc[12][7]=5;
	   	G->arc[7][13]=G->arc[12][7]=6; 	G->arc[7][14]=G->arc[14][7]=7;
	   
	   	G->arc[8][9]=G->arc[9][8]=2; 	G->arc[8][10]=G->arc[10][8]=2;
	   
	   	G->arc[9][10]=G->arc[10][9]=3;
	   
	   	G->arc[10][15]=G->arc[15][10]=1;
	   
	   	G->arc[11][12]=G->arc[12][11]=1;
	   
	   	G->arc[12][13]=G->arc[13][12]=1;
	   
	   	G->arc[13][14]=G->arc[14][13]=1; 	G->arc[13][16]=G->arc[16][13]=3;
	   
	   	G->arc[14][16]=G->arc[16][14]=2;
	   
	   	G->arc[15][16]=G->arc[16][15]=10;
	   
	   
	   	for(i = 0; i < G->numVertexes; i++) 
	   	{ 		
	   			for(j = i; j <    G->numVertexes; j++) 
	   			{ 			G->arc[j][i] =G->arc[i][j]; 		} 	
	   			}
	       }


	       /*  Dijkstra算法，求有向网G的v0顶点到其余顶点v的最短路径P[v]及带权长度D[v] */ /*     P[v]的值为前驱顶点下标,D[v]表示v0到v的最短路径长度和 */ 
	       void ShortestPath_Dijkstra(MGraph    G, int v0, Patharc *P, ShortPathTable    *D) 
	       { 	
				       int v,w,k,min; 	
				       int final[MAXVEX];/* 
				       final[w]=1表示求得顶点v0至vw的最短路径 */ 	
				       for(v=0; v

代码运行结果

2019.1.12第一篇CSDN文章。
这是我自己写的，函数参考了《大话数据结构》一书；
推荐给学数据结构的你。
坚持自己的学习之路。