【文献阅读】An Empirical Study of Spatial Attention Mechanisms in Deep Networks
论文链接:https://arxiv.org/abs/1904.05873
国内镜像:https://xxx.itp.ac.cn/abs/1904.05873
注意力机制使神经网络能够更多地关注输入的相关元素,而不是不相关的部分。
在计算给定query(例如,输出句子中的目标单词)的输出时,某些key(例如,输入句子中的源单词)将根据query按优先级排序。
在确定分配给给定query的某个key的注意权重时,通常只考虑输入的几个属性:
- query 的内容。对于self-attention的情况,
query内容可以是图像中query像素处的特征,也可以是一个句子中的一个单词的特征 - key 的内容。其中
key可以是query的本地邻域中的一个像素,也可以是句子中的另一个单词 - query 和 key 的相对位置
根据这些输入属性,有四种可能的 attention factors,可以从中确定key相对于query的注意权重:
ε1:the query and key content
ε2:the query content and relative position
ε3:the key content only
ε4:the relative position only

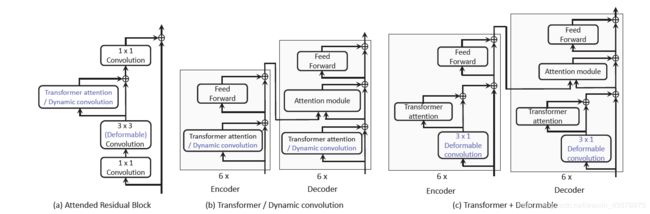
在这篇paper中,将Transformer attention、deformable convolution、dynamic convolution看作是空间注意力的各种实例化,涉及到 attention factors 的不同子集,并以不同的方式对这些因素进行解释。
广义注意力公式:
给定一个query和一组key,一个注意力函数根据衡量query-key的兼容性得到注意力权重,自适应的聚合key的内容。
y q = ∑ m = 1 M W m [ ∑ k ∈ Ω q A m ( q , k , z q , x k ) ⊙ W m ′ x k ] y_{q}=\sum_{m=1}^M W_{m} [\sum_{k \in \Omega_{q}} A_{m}(q, k, z_{q}, x_{k}) \odot W_{m}^{'} x_{k} ] yq=m=1∑MWm[k∈Ωq∑Am(q,k,zq,xk)⊙Wm′xk]
M M M是注意力头数, Ω q \Omega_{q} Ωq指定key的区域, A m ( q , k , z q , x k ) A_{m}(q, k, z_{q}, x_{k}) Am(q,k,zq,xk)是第m头的注意力权重, q q q是有内容 z q z_{q} zq的query的索引, k k k是有内容 x k x_{k} xk的key的索引, W m W_{m} Wm和 W m ′ W_{m}^{'} Wm′是可学习的权重。
归一化限制: ∑ k ∈ Ω q A m ( q , k , z q , x k ) = 1 \sum_{k \in \Omega_{q}} A_{m}(q, k, z_{q}, x_{k})=1 ∑k∈ΩqAm(q,k,zq,xk)=1
在 encoder-decoder attention 中,key和query来自两个不同的元素集。在大多数应用中,这两个元素集需要正确对齐。
在 self-attention 中,key和query来自同一组元素集。
将Transformer attention、deformable convolution、dynamic convolution看作是广义注意力公式的各种实例化
1.Transformer attention:
A m T r a n s ( q , k , z q , x k ) ∝ e x p ( ∑ j = 1 4 ϵ j ) A_{m}^{Trans}(q, k, z_{q}, x_{k}) \propto exp(\sum_{j=1}^{4}\epsilon_{j}) AmTrans(q,k,zq,xk)∝exp(j=1∑4ϵj)
ε1:
ε1衡量的是query和key内容的相似度:
ϵ 1 = ( U m z q ) T ( V m C x k ) \epsilon1=(U_{m} z_{q})^T (V_{m}^C x_{k}) ϵ1=(Umzq)T(VmCxk)
其中, U m U_{m} Um和 V m C V_m^C VmC分别是query和key内容的可学习的嵌入矩阵。
一个可能的结果是相似的query和key之间的一致性。
ε2:
ε2取决于query的内容和相对位置:
ϵ 1 = ( U m z q ) T ( V m R R k − q ) \epsilon1=(U_{m} z_{q})^T (V_{m}^R R_{k-q}) ϵ1=(Umzq)T(VmRRk−q)
其中, R k − q R_{k-q} Rk−q通过计算不同波长的正弦和余弦函数,将 k − q k−q k−q投射到高维空间中,从而对相对位置 k − q k−q k−q进行编码。
这可能有助于从图像识别的空间变换中分离出外观。
ε3:
ε3只取决于key的内容:
ϵ 3 = u m T V m C x k \epsilon3=u_{m}^T V_{m}^C x_{k} ϵ3=umTVmCxk
它捕获了任务应该关注的显著的key的内容,而与query无关。
ε4:
ε4只与相对位置有关:
ϵ 4 = v m T V m R R k − q \epsilon4=v_{m}^T V_{m}^R R_{k-q} ϵ4=vmTVmRRk−q
它捕获key和query之间的全局位置偏差。
在transformer attention中, W m W_{m} Wm和 W m ′ W_{m}^{'} Wm′都是可学习的。 W m ′ W_{m}^{'} Wm′将 x k x_{k} xk的特征映射到一个较低的维度以减少计算量; W m W_{m} Wm将聚合的特征重新映射回与 y q y_{q} yq相同的维度。
2.Regular and deformable convolution:
regular convolution和deformable convolution可以看作是空间注意力机制的特殊实例,是attention factors的子集。
regular convolution:
给定一个query,根据预先确定的相对于key的位置偏移量,对固定数量的key(例如,3×3)进行采样。
A m r e g u l a r ( q , k ) = { 1 , k = q + p m 0 , e l s e A_{m}^{regular}(q, k)= \left\{ \begin{aligned} 1, k = q+p_{m}\\ 0,else \end{aligned} \right. Amregular(q,k)={1,k=q+pm0,else
其中, p m p_{m} pm表示第 m m m个采样位置的偏移量。 W m ′ W_{m}^{'} Wm′固定为恒等式, W m W_{m} Wm是可学习的。
key的范围 Ω q \Omega_{q} Ωq被限制在一个以query位置为中心的局部窗口中,由卷积核大小决定。
在regular convolution中,attention factors仅取决于相对位置。
deformable convolution:
加入了可学习的偏移量来调整key的采样位置,从而捕获空间变换。可学习的偏移量是基于query内容进行预测的,因此对于输入是动态的。
key和query元素来自同一集合。它也可以作为self-attention的一个特殊实例。
A m d e f o r m ( q , k , x q ) = G ( k , q + p m + w m T x q ) A_{m}^{deform}(q, k, x_{q})=G(k, q+p_{m}+w_{m}^{T}x_{q}) Amdeform(q,k,xq)=G(k,q+pm+wmTxq)
其中, p m p_{m} pm是预先确定的偏移量; w m T x q w_{m}^{T}x_{q} wmTxq根据可学习的向量 w m w_{m} wm,投射query的内容 x q x_{q} xq到可变形的偏移; G ( a , b ) G(a,b) G(a,b)是 N N N维空间的双线性插值核,可以分解为 1 1 1维空间的双线性插值, G ( a , b ) = ∏ n = 1 N g ( a n , b n ) G(a,b)=\begin{matrix} \prod_{n=1}^N g(a_{n}, b_{n}) \end{matrix} G(a,b)=∏n=1Ng(an,bn), a n a_{n} an和 b n b_{n} bn指 a a a和 b b b分别的第 n n n维, g ( a n , b n ) = m a x ( 0 , 1 − ∣ a n − b n ∣ ) g(a_{n}, b_{n})=max(0, 1-|a_{n}-b_{n}|) g(an,bn)=max(0,1−∣an−bn∣)。
与regular convolution相似, W m ′ W_{m}^{'} Wm′也是恒等的。
在deformable convolution中,attention factors是query的内容和相对位置。
3.Dynamic convolution
它是建立在深度可分离的卷积与共享的动态内核权值的基础上,这些权值是基于query内容进行预测的。
在深度可分离卷积中,标准卷积被分解为深度卷积和1×1卷积,以减少计算量和模型大小。
在dynamic convolution中,根据输入特征动态预测深度卷积的核权值,然后进行Softmax归一化。
每个输入特征通道都有一个单独的注意力头:
y q = ∑ c = 1 C i n W c [ ∑ k ∈ Ω q A c d y n a m i c ( q , k , x q ) ⋅ x k , c ] y_{q}=\sum_{c=1}^{C_{in}}W_{c}[\sum_{k\in \Omega_{q}}A_{c}^{dynamic}(q, k, x_{q}) \cdot x_{k,c}] yq=c=1∑CinWc[k∈Ωq∑Acdynamic(q,k,xq)⋅xk,c]
其中, c c c是输入特征的通道, x k , c x_{k,c} xk,c是在 c c c通道上的特征值 x k x_{k} xk, W c W_{c} Wc是1x1的卷积。
A c d y n a m i c ( q , k , x q ) = { K j , c , k = q + p j 0 , e l s e A_{c}^{dynamic}(q, k, x_{q}) = \left\{ \begin{aligned} K_{j, c}, k = q+p_{j}\\ 0,else \end{aligned} \right. Acdynamic(q,k,xq)={Kj,c,k=q+pj0,else
其中, p j p_{j} pj是第 j j j个采样位置; K j , c K_{j, c} Kj,c是相应的核权值,由输入特征预测,并由同一组的通道共享。
K j , c = K j , g s h a r e ∝ e x p ( d j , g T x q ) , g = ⌈ c C i n / N g ⌉ K_{j,c}=K_{j,g}^{share} \propto exp(d_{j,g}^{T}x_{q}),g=\left \lceil \frac{c}{C_{in}/N_{g}} \right \rceil Kj,c=Kj,gshare∝exp(dj,gTxq),g=⌈Cin/Ngc⌉
输入特征被分为了 N g N_{g} Ng组( N g N_{g} Ng默认为16), K j , g s h a r e K_{j,g}^{share} Kj,gshare是第 g g g组的动态核权值, d j , g d_{j,g} dj,g是对应的可学习的权向量。
归一化: ∑ j = 1 N k K j , g s h a r e = 1 \sum_{j=1}^{N_{k}}K_{j,g}^{share}=1 ∑j=1NkKj,gshare=1, N k N_{k} Nk是动态核中的元素数量。
在dynamic convolution中,注意力分配是基于query内容和相对位置的。 Ω q \Omega_{q} Ωq是被动态核覆盖的query位置的一个局部窗口。
实验及分析:
复杂度:
在神经机器翻译中,key和query通常是一个句子中的几十个单词,因此ε1、ε2和ε4的计算开销与ε3相当。
在图像识别中,key和query由图像中的大量像素组成。因此,ε1、ε2和ε4的计算开销比ε3大得多。
与ε2相似,可变形卷积也是取决于query的内容和相对位置。但是可变形卷积仅对每个query的key的稀疏集进行采样,复杂度与query的数量成线性关系。因此,对于图像识别而言,可变形卷积的计算速度要比ε2快得多,并且在速度上与机器翻译的ε2相当。
动态卷积也是取决于query的内容和相对位置。计算开销与kernel size和query数的乘积成正比。与ε2项相比,如果kernel size比key数小得多,则计算开销可以大大降低。

表中, N s N_{s} Ns表示空间元素的数量(图像中的长x宽,文本中的字符数), C C C表示维度, N k N_{k} Nk是kernel size(默认图像中 N k N_{k} Nk= 3 x 3,文本中 N k N_{k} Nk= 3), N g N_{g} Ng表示动态卷积中特征组的数量。
实验网络设计:
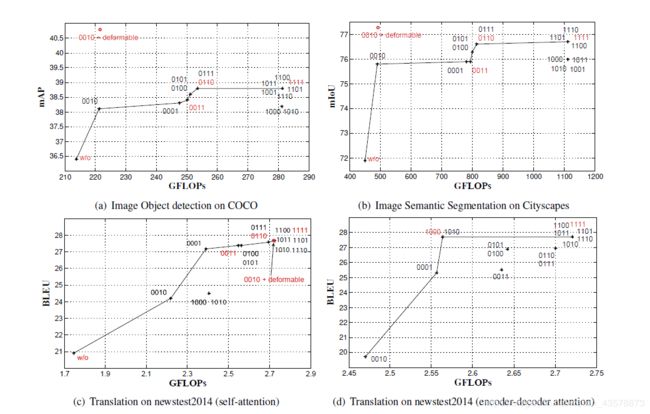
实验结果:
实验结论:
Transformer attention
- 在self-attention中,与
query无关相比,query敏感的作用较小。特别是query和key内容项对精度的影响很小,而在图像识别任务中计算量较大。删除它(从配置“1111”到“0111”)只会导致精度有微小的下降,同时大大减少了图像识别任务中的计算开销 - 在encoder-decoder attention中,
query和key内容项是至关重要的。仅使用query和key内容项(配置“1000”)能提供几乎与完整版本(配置“1111”)相同的准确性 - 在self-attention中,attention factors是①
query内容
与相对位置,②仅key内容是最重要的。相应的配置“0110”提供的精度非常接近完整版本(配置“1111”),同时在图像识别任务中节省了大量的计算开销。同样值得注意的是,只包含key内容(它捕获显著性信息)可以有效地提高性能,而不需要额外的开销
Deformable convolution vs. ε2 in Transformer attention
- 在目标检测和语义分割中,可变形卷积在精度和效率上都大大超过了ε2项。在效率方面,可变形卷积不需要遍历所有的
key。在精度方面,可变形卷积的双线性采样基于特征映射的局部线性假设。这种假设在局部图像内容逐渐变化的图像上比在文字突然变化的语言上更适用。 - 可变形卷积和
key内容项(“0010 +可变形”)的组合提供了最佳的精度和效率的权衡
Dynamic convolution vs. ε2 in Transformer attention
- 动态卷积在目标检测和语义分割方面效果不佳,其精度较低。在图像识别任务中,ε2项仍然在相同的空间范围内超过了动态卷积,并且计算量更小。