论文笔记：Understanding the Limitations of CNN-based Absolute Camera Pose Regression

摘要

Visual localization is the task of accurate camera pose estimation in a known scene. It is a key problem in computer vision and robotics, with applications including selfdriving cars, Structure-from-Motion, SLAM, and Mixed Reality. Traditionally, the localization problem has been tackled using 3D geometry. Recently, end-to-end approaches based on convolutional neural networks have become popular. These methods learn to directly regress the camera pose from an input image. However, they do not achieve the same level of pose accuracy as 3D structure-based methods. To understand this behavior, we develop a theoretical model for camera pose regression. We use our model to predict failure cases for pose regression techniques and verify our predictions through experiments. We furthermore use our model to show that pose regression is more closely related to pose approximation via image retrieval than to accurate pose estimation via 3D structure. A key result is that current approaches do not consistently outperform a handcrafted image retrieval baseline. This clearly shows that additional research is needed before pose regression algorithms are ready to compete with structure-based methods.

视觉定位是在已知场景下相机位姿准确估计任务。该任务在计算机视觉与机器人领域的关键问题，应用领域有自动驾驶、SFM和混合现实。传统方法中，3D 几何常用于解决该问题。近年来，基于CNN的端对端方法逐渐流行。这些方法从输入图像中直接回归相机的位姿。但是，这类方法很难达到与基于3D结构方法的位姿准确水平。为了理解这种现象，我们为相机位姿回归建立了一个理论模型。我们使用该模型预测了位姿归回技术失败的案例，并通过实验验证了我们的预测。我们进一步使用我们的模型展示了位姿回归更加与通过图像检索进行位姿逼近相关，而不是通过3D结构进行准确的位姿估计。一个重要的结论是**目前的方法并不是一直优胜于手工设计的图像检索的基线。**这清晰地表明了在位姿回归算法可以与基于结构的方法相竞争之前，仍然需要其他研究。

Introduction

视觉位姿定位的state-of-the-art算法遵循了基于3D结构的方法。第一步是确定了测试图像中像素与场景中3D点的对应关系。通过在RANSAC循环中使用PnP算法，这些对应关系然后用于确定相机的位姿。

这篇文章并没有提出一种新的absolute pose regression (APR)变形以缩小与基于结构方法在位姿准确度上差距，而是关注于理解APR技术与其性能。主要贡献有三：

1. 为绝对位姿估计（APR）建立了理论模型，展示了位姿回归更加与通过图像检索进行位姿逼近相关，而不是通过3D结构进行准确的位姿估计；
2. 从理论与实践上展示了APR方法不能保证具有超越训练集泛化能力，这点与基于结构的方法不同；
3. 考虑到APR与图像检索的密切联系，展示了目前的APR方法在性能上更加与手工设计的检索基线

A theory of Absolute Pose Regression

这节主要介绍了APR的理论模型。

标记

$\mathcal{I}$是一张以相机位姿${\mathbf{p}}_{\mathcal{I}}=({\mathbf{c}}_{\mathcal{I}},{\mathbf{r}}_{\mathcal{I}})$拍摄得到的图像。其中${\mathbf{c}}_{\mathcal{I}}\in {\mathbb{R}}^3$为相机，${\mathbf{r}}_{\mathcal{I}}\in {\mathbb{R}}^r$为相机旋转。相机的绝对位姿因此就表示为${\mathbb{R}}^{3+r}$空间中的一点。

绝对位姿回归

绝对位姿回归（APR）算法学习一个视觉定位函数$L(\mathcal{I})={\hat{\mathbf{p}}}_{\mathcal{I}}$，其中${\hat{\mathbf{p}}}_{\mathcal{I}}=({\hat{\mathbf{c}}}_{\mathcal{I}},{\hat{\mathbf{r}}}_{\mathcal{I}})$是对图像$\mathcal{I}$的相机位姿估计值。

APR是一个instance-level的问题。因此，对于APR，基于CNN的方法使用场景的一系列的图像，标记了它们的相对位姿，以作为训练集。训练目标是最小化损失$\mathcal{L}({\hat{\mathbf{p}}}_{\mathcal{I}},{\mathbf{p}}_{\mathcal{I}})$。

绝对位姿回归的理论

将APR分解为CNN的三个步骤：

1. 第一步表示为一个函数$F(\mathcal{I})$，从输入图像中提取特征；
2. 第二步计算特征的embedding$E(F(\mathcal{I}))$，用一个向量表示${\alpha }^{\mathcal{I}}=({\alpha }_1^{\mathcal{I}},\cdots ,{\alpha }_n^{\mathcal{I}}{)}^T\in {\mathbb{R}}^n$ 表示，这一步通常对应于位姿回归方法中的倒数第二步；
3. 最后一步将embedding 空间线性映射到相机的位姿空间，最后一步对应网络的最后一步。

将前两步视为一个单独的网络，可以得到训练得到的视觉位姿定位函数$L$：

$$\begin{array}{rl}L(\mathcal{I})& =\mathbf{b}+\mathrm{P}\cdot \mathrm{E}(\mathrm{F}(\mathcal{I}))\\ & =\mathbf{b}+\mathrm{P}\cdot ({\alpha }_1^{\mathcal{I}},\cdots ,{\alpha }_{\mathrm{n}}^{\mathcal{I}}{)}^{\mathrm{T}}\end{array}$$

其中$\mathrm{P}\in {\mathbb{R}}^{(3+\mathrm{r})\times \mathrm{n}}$ 是一个映射矩阵，$\mathbf{b}\in {\mathbb{R}}^{3+r}$为偏置项。输出项 $L(\mathcal{I})$为${\hat{\mathbf{p}}}_{\mathcal{I}}=({\hat{\mathbf{c}}}_{\mathcal{I}},{\hat{\mathbf{r}}}_{\mathcal{I}})$。
设${\mathbf{P}}_j\in {\mathbb{R}}^{3+r}$为矩阵$\mathrm{P}$ 的第$j$列。将预测的相机位姿表示为$\mathrm{P}$列的线性组合：

$$L(\mathcal{I})=\mathbf{b}+\sum _{j=1}^n{\alpha }_j^{\mathcal{I}}{\mathbf{P}}_j=({\hat{\mathbf{c}}}_{\mathcal{I}},{\hat{\mathbf{r}}}_{\mathcal{I}})$$

进一步将${\mathbf{P}}_j$分解为平移部分${\mathbf{c}}_j\in {\mathbb{R}}^3$和旋转部分 ${\mathbf{r}}_j\in {\mathbb{R}}^3$ ，因此${\mathbf{P}}_j=({\mathbf{c}}_{\mathbf{j}}^{\mathbf{T}},{\mathbf{r}}_{\mathbf{j}}^{\mathbf{T}}{)}^{\mathbf{T}}$。因此：

$$\left(\begin{array}{c}{\hat{\mathbf{c}}}_{\mathcal{I}}\\ {\hat{\mathbf{r}}}_{\mathcal{I}}\end{array}\right)=\left(\begin{array}{c}\widehat{{\mathbf{c}}_{\mathbf{b}}}+{\sum }_{j=1}^n{\alpha }_j^{\mathcal{I}}{\mathbf{c}}_j\\ \widehat{{\mathbf{r}}_{\mathbf{b}}}+{\sum }_{j=1}^n{\alpha }_j^{\mathcal{I}}{\mathbf{r}}_j\end{array}\right)$$

直观解释

基于CNN的位姿回归算法，例如PoseNet及其变种，学习得到了位姿基集合$\mathcal{B}=\{({\mathbf{c}}_{\mathbf{j}},{\mathbf{r}}_{\mathbf{j}})\}$，训练图像中所有的位姿都可以用这些位姿基的线性组合表示。基本上，网络通过学习将这些基通过embedding中的权重进行线性加权得到最终的绝对位姿。将$\{{\mathbf{c}}_{\mathbf{j}}\}$称为平移基。

与基于结构方法的比较

基于结构的方法能够成功估计相机位姿的必要条件是提供足够的正确的2D、3D匹配。基于CNN 的位姿回归方法能够学习得到由输入图像到相机位姿映射的必要条件是提供充足的训练数据。但是，收集数量巨大的图像，计算训练真值（通过sfm）并在很大的数据集上训练CNN是一个十分耗时的工作。接下来，使用理论模型预测了位姿回归方法在训练数据集有限的场景下失败的一些案例。此外，展示了基于结构的方法可以有效的处理这些案例。

实验配置

训练数据集与测试数据集中的真值都是由SfM方法得到。基于CNN的方法选择了具有代表性的PoseNet和MapNet，基于结构的方法选择了Active Search。Active Search 使用了Root-SIFT特征确定了2D-3D匹配关系，位姿估计由RANSAC循环中的P3P方法得到，再经过一个非线性的优化。

在一条直线或多个平行直线上获得的训练数据

$\mathcal{T}=\left\{(\mathcal{I},{\mathbf{p}}_{\mathcal{I}}=({\mathbf{c}}_{\mathcal{I}},{\mathbf{r}}_{\mathcal{I}}))\right\}$是一组训练图像以及对应的相机位姿。

在前一节提到，位姿回归中，相机位姿是由一组位姿基加权得到。考虑所有训练图像对应的相机位姿都在同一条直线上的场景。在该场景下，每个相机的位置${\mathbf{c}}_{\mathcal{I}}$对应与直线上的一点$\mathbf{o}+\delta \mathbf{d}$。其中，$\mathbf{o}\in {\mathbb{R}}^3$是直线上的一点，$\mathbf{d}\in {\mathbb{R}}^3$是直线的方向。训练中一个可能的解是所有的平移基${\mathbf{c}}_{\mathbf{j}}$都在一条只直线上，那么对于这个解，基于CNN的方法将无法泛化。

下图中两种实验场景说明这一点。其中训练和测试轨迹分别是红色和绿色，PoseNet、MapNet和Active Search的预测值分别为蓝色、紫色和蓝绿色。

可以看到，只有Active Search在两中场景下成功完成了预测，PoseNet、MapNet在考虑到相机抖动的情况下都没有实现泛化。

更常规的轨迹

考虑由训练图像子集${\mathcal{T}}^{\prime }=\mathcal{I}$定义的场景部分${\mathcal{P}}^{\prime }$。子集${\mathcal{B}}^{\prime }({\mathcal{P}}^{\prime })$对应位姿基$\mathcal{B}=\{({\mathbf{c}}_j,{\mathbf{r}}_j)\}$中的部分为：

$${\mathcal{B}}^{\prime }({\mathcal{P}}^{\prime })=\left\{({\mathbf{c}}_{\mathbf{j}},{\mathbf{r}}_{\mathbf{j}})|\mathbf{e}\mathbf{x}\mathbf{i}\mathbf{s}\mathbf{t}\mathbf{s}\mathcal{I}\in {\mathcal{T}}^{\prime }\mathbf{w}\mathbf{i}\mathbf{t}\mathbf{h}\Vert {\mathbf{a}}_{\mathbf{j}}^{\mathcal{I}}\Vert >0\right\}$$

泛化的一个强必要条件是每个${\mathcal{B}}^{\prime }({\mathcal{P}}^{\prime })$的线性张成包含测试图像集合${\mathcal{P}}^{\prime 3}$中对应的所有位姿。在实际实验中并不能保证这种情况。

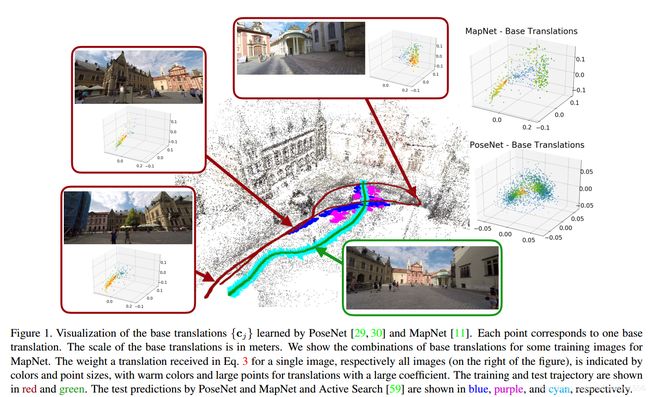
图1和图3展示了更加常规的轨迹。可以看到：

1. 所有的平移基都在一个平面上，因为训练图像的拍摄位置都在同一个平面上；
2. 当测试轨迹与训练轨迹相交时，网络泛化的很好；在其他情况下，预测的测试位姿都是更加解决具有相似外观的训练图像中的位姿。场景下，训练得到的平移基不能准确的对测试位置进行建模，这表明了需要更多的训练数据。
3. 当测试图像与训练图像有较少的视觉重合时，基于结构的Active Search方法失败或提供了不足够准确的解，由于没有足够的匹配对。

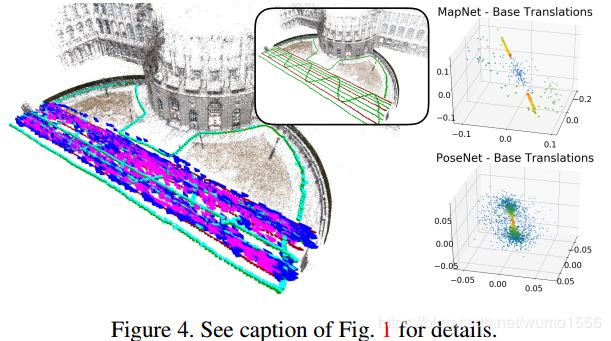
图4展示了一个更加复杂的实验，其中训练轨迹是多个平行的直线，测试轨迹包括了一些平行直线、穿插在训练轨迹间的曲线以及一些训练视场内的曲线组成。可以看到

1. 基于CNN的方法可以预测靠近训练轨迹的部分图像，但是很难对在其之间的测试位姿进行插值，没有实现泛化。
2. Active Search方法几乎解决了训练与测试图像有较大视角变化的情况，但当这种变化太大时难以提供足够的匹配以实现位姿估计。因此基于结构的方法的发展更加依赖于对大视角变化更加鲁棒的局部特征。

使用密集采样的训练数据

由于密集采样设计到大量数据，这小节的实验使用了仿真数据。验证了随着训练数据的增加，PoseNet和MapNet的性能都有所提升，但是仍然没有超过Active Search。

结论

在训练数据较少以及视角变化较大的情况下，位姿回归技术性能不佳。这限制了其在实际中的应用。尽管提供了充足的训练数据，位姿回归方法仍然没能达到与基于结构的方法相同的性能。事实上，基于结构的方法遵循了摄影几何的规律，并且强调了场景的3D结构。

与图像检索的比较

前面展示了在训练数据较少的情况下，APR技术得到的测试图像预测值往往比较与训练集相近。这点与图像检索比较相似。这不是巧合，事实上，APR与图像检索有着很强的联系。

设$\mathcal{I}$ 为一张测试图像，$\mathcal{J}$为一训练图像，两者具有同一场景的相同部分。记${\alpha }^{\mathcal{I}}={\alpha }^{\mathcal{J}}+{\Delta }^{\mathcal{I}}$。因此，$\mathcal{I}$的位姿估计值$({\hat{\mathbf{c}}}_{\mathcal{I}},{\hat{\mathbf{r}}}_{\mathcal{I}})$与$\mathcal{J}$的位姿估计值$({\hat{\mathbf{c}}}_{\mathcal{J}},{\hat{\mathbf{r}}}_{\mathcal{J}})$的关系为：

$$\left(\begin{array}{c}{\hat{\mathbf{c}}}_{\mathcal{I}}\\ {\hat{\mathbf{r}}}_{\mathcal{I}}\end{array}\right)=\left(\begin{array}{c}{\hat{\mathbf{c}}}_{\mathcal{J}}\\ {\hat{\mathbf{r}}}_{\mathcal{J}}\end{array}\right)+\left(\begin{array}{c}{\sum }_{j=1}^n{\Delta }_j^{\mathcal{I}}{\mathbf{c}}_{\mathcal{I}}\\ {\sum }_{j=1}^n{\Delta }_j^{\mathcal{I}}{\mathbf{r}}_{\mathcal{I}}\end{array}\right)=\left(\begin{array}{c}{\hat{\mathbf{c}}}_{\mathcal{J}}\\ {\hat{\mathbf{r}}}_{\mathcal{J}}\end{array}\right)+\left(\begin{array}{c}{\hat{\mathbf{c}}}_{\mathcal{I},\mathcal{J}}\\ {\hat{\mathbf{r}}}_{\mathcal{I},\mathcal{J}}\end{array}\right)$$

其中$({\hat{\mathbf{c}}}_{\mathcal{I},\mathcal{J}},{\hat{\mathbf{r}}}_{\mathcal{I},\mathcal{J}})$是$\mathcal{I}$的位姿相对于$\mathcal{J}$位姿的预测值的预测值。

标准的图像记过方法首先找到与给定测试图像$\mathcal{I}$最相似的训练图像$\mathcal{J}$，其相似度的定义有一些特征空间定义，例如词袋(Bag-of-Words)或VLDA。然后，测试图像的位姿由检索得到的图像位姿逼近得到，即$({\hat{\mathbf{c}}}_{\mathcal{I}},{\hat{\mathbf{r}}}_{\mathcal{I}})=({\hat{\mathbf{c}}}_{\mathcal{J}},{\hat{\mathbf{r}}}_{\mathcal{J}})$，没有添加便宜项。但是，检索方法可以由检索得到的前k个训练图像的位姿的仿射组合提供偏置项，即${\sum }_{j=1}^k{a}_i({\mathbf{c}}_{{\mathcal{J}}_i},{\mathbf{r}}_{{\mathcal{J}}_i}),\sum a_j=1$。设检索过程中的$\mathcal{I}$的描述子为$\mathbf{d}(\mathcal{I})$。权重$a_j$可以由最小化$\Vert \mathbf{d}(\mathcal{I})-{\sum }_{i=1}^k{a}_i\mathbf{d}({\mathcal{J}}_i)\Vert$得到。

这种插值方法与基于CNN的位姿回归方法中位姿基线性组合方法比较类似。

实验比较

进行了四组实验，分别是

1. Cambridge Landmarks 和 7 Scens 数据集，纹理较丰富，有利于SIFT，训练集与测试集位姿差异较大
2. TUM LSI 数据集，纹理较差
3. RobotCar数据集
4. 密集采样数据集，仿真生成

这四组实验都从表明了APR方法最好不会超过图像检索（在密集采样、训练数据较多时可能超过），其性能更加接近与检索的基线而不是基于结构的方法。

结论

1. 提出了APR的理论模型，并分析了APR什么能干什么不能干，分析了APR不能泛化的原因，
2. 说明了APR更加类似与逼近测试位姿的图像检索而不是较为准确的估计位姿的基于结构的方法，而且展示了没有一种位姿回归方法可以达到基于结构方法的基线。
3. 在基于CNN的回归方法可以实用之前，仍然需要大量的工作。