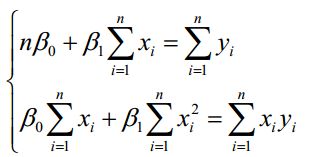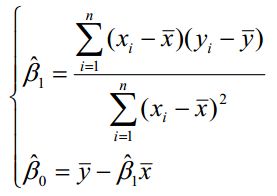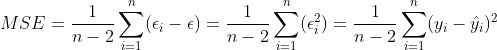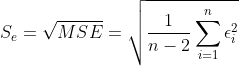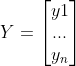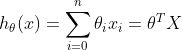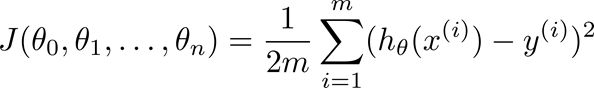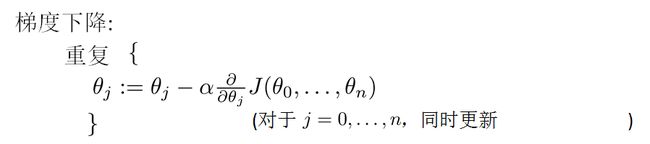SparkML之回归(一)线性回归

----------------------------目录-----------------------------------------------------------------------

线性回归理论

spark源码

Spark实验

-------------------------------------------------------一元线性回归-------------------------------------------------------------------------

模型

反应一个因变量与一个自变量之间的线性关系，一元线性回归模型如下：

                                                         （1）

其中：

、：回归系数

：自变量

：因变量

：随机误差，一般假设服从

那么可以得到结论就是：服从

若我们之前对 (,)进行了 n次观测，那么就可以得到如下，一系列的数据

  为(1,2,...n)

那么把這些数值，带入(1)公式，那么就有 n个包含、方程，大家知道当要确定n个参数的时候，满秩的情况下，只要n个方程就就可以确定了，那么如何根据历史的观测数据来选择，来选择最佳的、，只要把、确定了，那么我们随便输入一个，就可以得到一个，那么选择一个"未来"的,就可以计算一个"未来"的,那么就达到了预测效果

普通最小二乘法

那么什么才是最佳的 、，最小二乘法的思想就是把决定后的方程，代入参数使得方差最小，就是最佳的。我们把全部的方差记为:

                               

那么现在就是计算关于参数、的极小值，当关于参数、的偏导为0的时候，那么取到极值

           

对其进行整理，得到如下：

              

那么可以直接计算出：

当自变量x多的时候，就很难直接计算、、....、，那么就必须用克拉姆法则（Cramer's Rule）计算，

其中，、、、是、、....、的最小二乘估计。

拟合效果分析

1、残差的样本方差

残差: （i = 1，2，...n）

残差的样本均值：

那么残差的样本方差:

其中n-2是自由度，因为有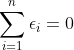和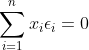约束，所以自由度减2（残差之间相互独立，残差和自变量x相互独立），如果我们的拟合方程：解释因变量越强，那么MSE是越小。你会发现：

这个MSE就是总体回归模型中方差的无偏估计量。

那么它的标准差：

2、判定系数（R）

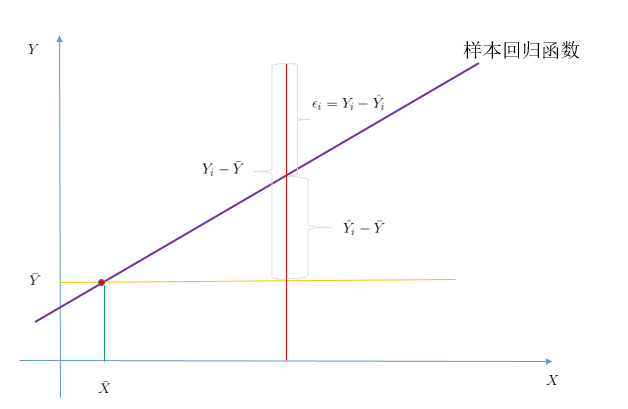
我们从新考虑我们的样本回归函数：

因为我们的解释变量的平均值,一定会经过我们的样本回归函数，下面证明：

两边进行平方之后再加总，然后除以样本容量n：

其中，，得到：

下面结合图像进行说明：

结合图像，我们可以得到下面方程：

两边平方之后，进行加总，得到：

:样本观测值和其平均值的离差平方和，自由度为n-1

:拟合直线可解释部分的平方和，自由度为1

:样本的观测值和估计值之差的平方，既残差平方和，自由度为n-2

缩写全拼（采用国外教材的缩写方式）：

Total sum of squares（SST）：总离差平方和

Residual sum of squares (SSR)：残差平方和

explained sum of squares(SSE):回归平方和（国人根据实际意义自己命名的？）

所以我们有：

那么对于我们真正解释了的部分和总体的比值（用表示）：

当时，也就是SSR = SSE,那么就是说原始数据完全可以拟合值来解释，此时SSR = 0，那么拟合非常完美

一般。

SSR很好计算，就是样本的实际观察值与估计值差的平方，所以用SSR去计算R

显著性检验

当你拟合好参数的时候，你要去评定一个這样的一个模型对于我们想要解释的问题是否显著(只有R是不够的)，

如果不显著那么就需要换其他模型方法了。对于其中检验的方法有F检验和T检验，本文重点是SparkMlib下的线性回归，本节只是一个铺垫，所以具体如何检验，就不赘述了。

-------------------------------------------------------多元线性回归----------------------------------------------------------------------------

模型

反应多个因变量与一个自变量之间的线性关系，多元线性回归模型如下：

 （2）

其中：，都是与无关的未知参数，是回归系数。

现在得到n个样本数据（）,=1,....,n,其中,那么（2）得到：

（3）

我们可以把（3）写成如下模式：

（4）

其中：

,,,

求解过程和一元线性回归一样，可以得到:

判定系数（R）还是按照一元回归那样求解，当R大于0.8才认为线性关系明显

===================================最小二乘法的缺陷============================

1、只有当X满秩的时候，才可以用最小二乘法。因为在求解的时候的条件：X是满秩的，也就是在决定多个因变量

必须是相互独立的，当如果和有关联，可以用表示，那么X就不是满秩的

此时用最小二乘法就是错误的，因为X是不可逆的

2、最小二乘的复杂度高，在处理大规模数据的时候，耗时长。

--------------------------------------------------------------------梯度下降法-------------------------------------------------------------------

由于最小二乘法在求解时，存在局限，所以在计算机领域一般采用梯度下降法，来近似求解

为了与文献2的符号一致，所以放弃前面用过的符号，采用文献2中的符号。现在直接从多元线性回归开始

线性方程：

我们让,那么方程变为：

若我们之前对 (,)进行了 m次观测，那么就可以得到如下，一系列的数据

  为(1,2,...m),按照前面的思路，我们来计算“相差”多少,既所说的cost function：

（小插曲：不知道为什么有很多人把上面的m给省略了，在andrew NG课程中和Spark源码理解中都有这个m

其实加上m更能体现问题）

也就说让最小。如果用之前的最小二乘法，那么就是，让对求偏导，让等式都等于0，建立方程，联合求解：

我们知道最小二乘法的弊端，所以采用梯度下降法来求解最优的:

其中是学习效率，而且迭代的初始值设置为n+1列的零向量，然后一直迭代，直到收敛为止。

当样本很大的时候，如果迭代次数很大，那么我们会选择一部分样本进行对的更新计算。

更多细节，请看：http://blog.csdn.net/legotime/article/details/51277141

-------------------------------------------------------------------------------------------------------------------------------------------------

Spark源码

package org.apache.spark.mllib.regression包含了两个部分：LinearRegressionModel和LinearRegressionWithSGD

1、回归的模型（class和object），class 的参数是继承GeneralizedLinearModel广义回归模型，之后形成一个完整的

线性回归模型，object上面的方法用于导出已经保存的模型进行回归

2、LinearRegressionWithSGD：随机梯度下降法，cost  function：f(weights) = 1/n ||A weights-y||^2也就是前面

记住这个还是加上m更能体现问题，（除以m表示均方误差）

LinearRegressionWithSGD是继承GeneralizedLinearAlgorithm[LinearRegressionModel]广义回归类

1、回归模型源码如下

/**
 * Regression model trained using LinearRegression.
 *
 * @param weights Weights computed for every feature.(每个特征的权重向量)
 * @param intercept Intercept computed for this model.（此模型的偏置或残差）
 *
 */
@Since("0.8.0")
class LinearRegressionModel @Since("1.1.0") (
    @Since("1.0.0") override val weights: Vector,
    @Since("0.8.0") override val intercept: Double)
  extends GeneralizedLinearModel(weights, intercept) with RegressionModel with Serializable
  with Saveable with PMMLExportable {

  //进行预测:Y = W*X+intercept
  override protected def predictPoint(
      dataMatrix: Vector,
      weightMatrix: Vector,
      intercept: Double): Double = {
    weightMatrix.toBreeze.dot(dataMatrix.toBreeze) + intercept
  }
  //模型保存包含：保存的位置，名字，权重和偏置
  @Since("1.3.0")
  override def save(sc: SparkContext, path: String): Unit = {
    GLMRegressionModel.SaveLoadV1_0.save(sc, path, this.getClass.getName, weights, intercept)
  }

  override protected def formatVersion: String = "1.0"
}
//加载上面保存和的模型，用load（sc,存储路径）
@Since("1.3.0")
object LinearRegressionModel extends Loader[LinearRegressionModel] {

  @Since("1.3.0")
  override def load(sc: SparkContext, path: String): LinearRegressionModel = {
    val (loadedClassName, version, metadata) = Loader.loadMetadata(sc, path)
    // Hard-code class name string in case it changes in the future
    val classNameV1_0 = "org.apache.spark.mllib.regression.LinearRegressionModel"
    (loadedClassName, version) match {
      case (className, "1.0") if className == classNameV1_0 =>
        val numFeatures = RegressionModel.getNumFeatures(metadata)
        val data = GLMRegressionModel.SaveLoadV1_0.loadData(sc, path, classNameV1_0, numFeatures)
        new LinearRegressionModel(data.weights, data.intercept)
      case _ => throw new Exception(
        s"LinearRegressionModel.load did not recognize model with (className, format version):" +
        s"($loadedClassName, $version).  Supported:\n" +
        s"  ($classNameV1_0, 1.0)")
    }
  }
}

2、LinearRegressionWithSGD类，该类是基于无正规化的随机梯度下降，而且是继承GeneralizedLinearAlgorithm[LinearRegressionModel]广义回归类

/**
 * Train a linear regression model with no regularization using Stochastic Gradient Descent.
 * This solves the least squares regression formulation
 *              f(weights) = 1/n ||A weights-y||^2^
 * (which is the mean squared error).
 * Here the data matrix has n rows, and the input RDD holds the set of rows of A, each with
 * its corresponding right hand side label y.
 * See also the documentation for the precise formulation.
 */
@Since("0.8.0")
class LinearRegressionWithSGD private[mllib] (
    private var stepSize: Double,//步长
    private var numIterations: Int,//迭代次数
    private var miniBatchFraction: Double)//参与迭代样本的比列
  extends GeneralizedLinearAlgorithm[LinearRegressionModel] with Serializable {

  private val gradient = new LeastSquaresGradient()  //阅读:3
  private val updater = new SimpleUpdater()  //阅读：4
  @Since("0.8.0")
  override val optimizer = new GradientDescent(gradient, updater) //阅读：5
    .setStepSize(stepSize)
    .setNumIterations(numIterations)
    .setMiniBatchFraction(miniBatchFraction)

  /**
   * Construct a LinearRegression object with default parameters: {stepSize: 1.0,
   * numIterations: 100, miniBatchFraction: 1.0}.
   */
  @Since("0.8.0")
  def this() = this(1.0, 100, 1.0) 

  override protected[mllib] def createModel(weights: Vector, intercept: Double) = {
    new LinearRegressionModel(weights, intercept)
  }
}

/**
 * Top-level methods for calling LinearRegression.
 *
 */
@Since("0.8.0")
object LinearRegressionWithSGD {

  /**
   * Train a Linear Regression model given an RDD of (label, features) pairs. We run a fixed number
   * of iterations of gradient descent using the specified step size. Each iteration uses
   * `miniBatchFraction` fraction of the data to calculate a stochastic gradient. The weights used
   * in gradient descent are initialized using the initial weights provided.
   *
   * @param input RDD of (label, array of features) pairs. Each pair describes a row of the data
   *              matrix A as well as the corresponding right hand side label y
   * @param numIterations Number of iterations of gradient descent to run.
   * @param stepSize Step size to be used for each iteration of gradient descent.
   * @param miniBatchFraction Fraction of data to be used per iteration.
   * @param initialWeights Initial set of weights to be used. Array should be equal in size to
   *        the number of features in the data.
   *
   */
  @Since("1.0.0")
  def train(
      input: RDD[LabeledPoint],
      numIterations: Int,
      stepSize: Double,
      miniBatchFraction: Double,
      initialWeights: Vector): LinearRegressionModel = {
    new LinearRegressionWithSGD(stepSize, numIterations, miniBatchFraction)
      .run(input, initialWeights)
  }

  /**
   * Train a LinearRegression model given an RDD of (label, features) pairs. We run a fixed number
   * of iterations of gradient descent using the specified step size. Each iteration uses
   * `miniBatchFraction` fraction of the data to calculate a stochastic gradient.
   *
   * @param input RDD of (label, array of features) pairs. Each pair describes a row of the data
   *              matrix A as well as the corresponding right hand side label y
   * @param numIterations Number of iterations of gradient descent to run.
   * @param stepSize Step size to be used for each iteration of gradient descent.
   * @param miniBatchFraction Fraction of data to be used per iteration.
   *
   */
  @Since("0.8.0")
  def train(
      input: RDD[LabeledPoint],
      numIterations: Int,
      stepSize: Double,
      miniBatchFraction: Double): LinearRegressionModel = {
    new LinearRegressionWithSGD(stepSize, numIterations, miniBatchFraction).run(input)
  }

  /**
   * Train a LinearRegression model given an RDD of (label, features) pairs. We run a fixed number
   * of iterations of gradient descent using the specified step size. We use the entire data set to
   * compute the true gradient in each iteration.
   *
   * @param input RDD of (label, array of features) pairs. Each pair describes a row of the data
   *              matrix A as well as the corresponding right hand side label y
   * @param stepSize Step size to be used for each iteration of Gradient Descent.
   * @param numIterations Number of iterations of gradient descent to run.
   * @return a LinearRegressionModel which has the weights and offset from training.
   *
   */
  @Since("0.8.0")
  def train(
      input: RDD[LabeledPoint],
      numIterations: Int,
      stepSize: Double): LinearRegressionModel = {
    train(input, numIterations, stepSize, 1.0)
  }

  /**
   * Train a LinearRegression model given an RDD of (label, features) pairs. We run a fixed number
   * of iterations of gradient descent using a step size of 1.0. We use the entire data set to
   * compute the true gradient in each iteration.
   *
   * @param input RDD of (label, array of features) pairs. Each pair describes a row of the data
   *              matrix A as well as the corresponding right hand side label y
   * @param numIterations Number of iterations of gradient descent to run.
   * @return a LinearRegressionModel which has the weights and offset from training.
   *
   */
  @Since("0.8.0")
  def train(
      input: RDD[LabeledPoint],
      numIterations: Int): LinearRegressionModel = {
    train(input, numIterations, 1.0, 1.0)
  }
}

3、最小平方梯度，首先联系我们的代价（损失）函数，如下：

损失函数源码标记为：L = 1/2n ||A weights-y||^2

每个样本的梯度值：

每个样本的误差值：

第一个compute返回的是 ,第二个compute返回的是

class LeastSquaresGradient extends Gradient {
  override def compute(data: Vector, label: Double, weights: Vector): (Vector, Double) = {
    val diff = dot(data, weights) - label
    val loss = diff * diff / 2.0//误差
    val gradient = data.copy
    scal(diff, gradient)////梯度值x*(y-h(x))
    (gradient, loss)
  }

  override def compute(
      data: Vector,
      label: Double,
      weights: Vector,
      cumGradient: Vector): Double = {
    val diff = dot(data, weights) - label//h(x)-y
    axpy(diff, data, cumGradient)//y = x*(h(x)-y)+cumGradient
    /**axpy用法：
      * Computes y += x * a, possibly doing less work than actually doing that operation
      *  def axpy[A, X, Y](a: A, x: X, y: Y)(implicit axpy: CanAxpy[A, X, Y]) { axpy(a,x,y) }
      */
    diff * diff / 2.0
  }
}

4、权重更新（SimpleUpdater）,更新公式如下：

返回的时候偏置项设置为0了

class SimpleUpdater extends Updater {
  override def compute(
      weightsOld: Vector,//上一次计算后的权重向量
      gradient: Vector,//本次迭代的权重向量
      stepSize: Double,//步长
      iter: Int,//当前迭代次数
      regParam: Double): (Vector, Double) = {
    val thisIterStepSize = stepSize / math.sqrt(iter)//学习速率  a
    val brzWeights: BV[Double] = weightsOld.toBreeze.toDenseVector
    brzAxpy(-thisIterStepSize, gradient.toBreeze, brzWeights)
    //brzWeights + = gradient.toBreeze-thisIterStepSize

    (Vectors.fromBreeze(brzWeights), 0)
  }
}

5权重优化

权重优化采用的是随机梯度降，但是默认的是miniBatchFraction= 1.0。

/**
 * Class used to solve an optimization problem using Gradient Descent.
 * @param gradient Gradient function to be used.
 * @param updater Updater to be used to update weights after every iteration.
 */
class GradientDescent private[spark] (private var gradient: Gradient, private var updater: Updater)
  extends Optimizer with Logging {

  private var stepSize: Double = 1.0
  private var numIterations: Int = 100
  private var regParam: Double = 0.0
  private var miniBatchFraction: Double = 1.0
  private var convergenceTol: Double = 0.001//收敛公差

  /**
   * Set the initial step size of SGD for the first step. Default 1.0.
   * In subsequent steps, the step size will decrease with stepSize/sqrt(t)
   */
  def setStepSize(step: Double): this.type = {
    this.stepSize = step
    this
  }

  /**
   * :: Experimental ::
   * Set fraction of data to be used for each SGD iteration.
   * Default 1.0 (corresponding to deterministic/classical gradient descent)
   */
  @Experimental
  def setMiniBatchFraction(fraction: Double): this.type = {
    this.miniBatchFraction = fraction
    this
  }

  /**
   * Set the number of iterations for SGD. Default 100.
   */
  def setNumIterations(iters: Int): this.type = {
    this.numIterations = iters
    this
  }

  /**
   * Set the regularization parameter. Default 0.0.
   */
  def setRegParam(regParam: Double): this.type = {
    this.regParam = regParam
    this
  }

  /**
   * Set the convergence tolerance. Default 0.001
   * convergenceTol is a condition which decides iteration termination.
   * The end of iteration is decided based on below logic.
   *
   *  - If the norm of the new solution vector is >1, the diff of solution vectors
   *    is compared to relative tolerance which means normalizing by the norm of
   *    the new solution vector.
   *  - If the norm of the new solution vector is <=1, the diff of solution vectors
   *    is compared to absolute tolerance which is not normalizing.
   *
   * Must be between 0.0 and 1.0 inclusively.
   */
  def setConvergenceTol(tolerance: Double): this.type = {
    require(0.0 <= tolerance && tolerance <= 1.0)
    this.convergenceTol = tolerance
    this
  }

  /**
   * Set the gradient function (of the loss function of one single data example)
   * to be used for SGD.
   */
  def setGradient(gradient: Gradient): this.type = {
    this.gradient = gradient
    this
  }


  /**
   * Set the updater function to actually perform a gradient step in a given direction.
   * The updater is responsible to perform the update from the regularization term as well,
   * and therefore determines what kind or regularization is used, if any.
   */
  def setUpdater(updater: Updater): this.type = {
    this.updater = updater
    this
  }

  /**
   * :: DeveloperApi ::
   * Runs gradient descent on the given training data.
   * @param data training data
   * @param initialWeights initial weights
   * @return solution vector
   */
  @DeveloperApi
  def optimize(data: RDD[(Double, Vector)], initialWeights: Vector): Vector = {
    val (weights, _) = GradientDescent.runMiniBatchSGD(
      data,
      gradient,
      updater,
      stepSize,
      numIterations,
      regParam,
      miniBatchFraction,
      initialWeights,
      convergenceTol)
    weights
  }

}

/**
 * :: DeveloperApi ::
 * Top-level method to run gradient descent.
 */
@DeveloperApi
object GradientDescent extends Logging {
  /**
   * Run stochastic gradient descent (SGD) in parallel using mini batches.
   * In each iteration, we sample a subset (fraction miniBatchFraction) of the total data
   * in order to compute a gradient estimate.
   * Sampling, and averaging the subgradients over this subset is performed using one standard
   * spark map-reduce in each iteration.
   *
   * @param data Input data for SGD. RDD of the set of data examples, each of
   *             the form (label, [feature values]).
   * @param gradient Gradient object (used to compute the gradient of the loss function of
   *                 one single data example)
   * @param updater Updater function to actually perform a gradient step in a given direction.
   * @param stepSize initial step size for the first step
   * @param numIterations number of iterations that SGD should be run.
   * @param regParam regularization parameter
   * @param miniBatchFraction fraction of the input data set that should be used for
   *                          one iteration of SGD. Default value 1.0.
   * @param convergenceTol Minibatch iteration will end before numIterations if the relative
   *                       difference between the current weight and the previous weight is less
   *                       than this value. In measuring convergence, L2 norm is calculated.
   *                       Default value 0.001. Must be between 0.0 and 1.0 inclusively.
   * @return A tuple containing two elements. The first element is a column matrix containing
   *         weights for every feature, and the second element is an array containing the
   *         stochastic loss computed for every iteration.
   */
  def runMiniBatchSGD(
      data: RDD[(Double, Vector)],
      gradient: Gradient,
      updater: Updater,
      stepSize: Double,
      numIterations: Int,
      regParam: Double,
      miniBatchFraction: Double,
      initialWeights: Vector,
      convergenceTol: Double): (Vector, Array[Double]) = {

    // convergenceTol should be set with non minibatch settings
    if (miniBatchFraction < 1.0 && convergenceTol > 0.0) {
      logWarning("Testing against a convergenceTol when using miniBatchFraction " +
        "< 1.0 can be unstable because of the stochasticity in sampling.")
    }
    //把历史的权重放在一个数组中
    val stochasticLossHistory = new ArrayBuffer[Double](numIterations)
    // Record previous weight and current one to calculate solution vector difference
    //初始化权重
    var previousWeights: Option[Vector] = None
    var currentWeights: Option[Vector] = None
    //训练的样本数
    val numExamples = data.count()

    // if no data, return initial weights to avoid NaNs
    if (numExamples == 0) {
      logWarning("GradientDescent.runMiniBatchSGD returning initial weights, no data found")
      return (initialWeights, stochasticLossHistory.toArray)
    }

    if (numExamples * miniBatchFraction < 1) {
      logWarning("The miniBatchFraction is too small")
    }

    // Initialize weights as a column vector
    var weights = Vectors.dense(initialWeights.toArray)
    val n = weights.size

    /**
     * For the first iteration, the regVal will be initialized as sum of weight squares
     * if it's L2 updater; for L1 updater, the same logic is followed.
     */
    var regVal = updater.compute(
      weights, Vectors.zeros(weights.size), 0, 1, regParam)._2

    var converged = false // indicates whether converged based on convergenceTol判断是否收敛
    var i = 1
    while (!converged && i <= numIterations) {
      //广播weights
      val bcWeights = data.context.broadcast(weights)

      // Sample a subset (fraction miniBatchFraction) of the total data
      // compute and sum up the subgradients on this subset (this is one map-reduce)
      val (gradientSum, lossSum, miniBatchSize) = data.sample(false, miniBatchFraction, 42 + i)
        .treeAggregate((BDV.zeros[Double](n), 0.0, 0L))(
          seqOp = (c, v) => {
            // c: (grad, loss, count), v: (label, features)
            val l = gradient.compute(v._2, v._1, bcWeights.value, Vectors.fromBreeze(c._1))
            (c._1, c._2 + l, c._3 + 1)
          },
          combOp = (c1, c2) => {
            // c: (grad, loss, count)
            (c1._1 += c2._1, c1._2 + c2._2, c1._3 + c2._3)
          })

      if (miniBatchSize > 0) {
        /**
         * lossSum is computed using the weights from the previous iteration
         * and regVal is the regularization value computed in the previous iteration as well.
         */
        //保存误差，更新权重
        stochasticLossHistory.append(lossSum / miniBatchSize + regVal)
        val update = updater.compute(
          weights, Vectors.fromBreeze(gradientSum / miniBatchSize.toDouble),
          stepSize, i, regParam)
        weights = update._1
        regVal = update._2

        previousWeights = currentWeights
        currentWeights = Some(weights)
        if (previousWeights != None && currentWeights != None) {
          converged = isConverged(previousWeights.get,
            currentWeights.get, convergenceTol)
        }
      } else {
        logWarning(s"Iteration ($i/$numIterations). The size of sampled batch is zero")
      }
      i += 1
    }

    logInfo("GradientDescent.runMiniBatchSGD finished. Last 10 stochastic losses %s".format(
      stochasticLossHistory.takeRight(10).mkString(", ")))
    //返回权重和历史误差数组
    (weights, stochasticLossHistory.toArray)

  }

SparkML实验：

package Regression

import org.apache.spark.mllib.linalg.Vectors
import org.apache.spark.mllib.regression.{LabeledPoint, LinearRegressionModel, LinearRegressionWithSGD}
import org.apache.spark.{SparkConf, SparkContext}


object RegressionWithSGD {
  def main(args: Array[String]) {
   val conf = new SparkConf().setAppName("LinearRegressionWithSGDExample").setMaster("local")
    val sc = new SparkContext(conf)

    // Load and parse the data
    val data = sc.textFile("E:\\SparkCore2\\data\\mllib\\ridge-data\\lpsa.data")
    val parsedData = data.map { line =>
      val parts = line.split(',')
      LabeledPoint(parts(0).toDouble, Vectors.dense(parts(1).split(' ').map(_.toDouble)))
    }
    /**parsedData形式：
      * (-0.4307829,[-1.63735562648104,-2.00621178480549,-1.86242597251066,-1.02470580167082,-0.522940888712441,
      * -0.863171185425945,-1.04215728919298,-0.864466507337306])
      */

    // Building the model
    val numIterations = 100//迭代次数
    val stepSize = 0.00000001//步长
    val model = LinearRegressionWithSGD.train(parsedData, numIterations, stepSize)//训练模型

    // Evaluate model on training examples and compute training error
    val valuesAndPreds = parsedData.map { point =>
      val prediction = model.predict(point.features)
      (point.label, prediction)
    }
    val numCount = valuesAndPreds.count()
    println("The sample count"+numCount)

    val MSE = valuesAndPreds.map{ case(v, p) => math.pow((v - p), 2) }.mean()//残差的样本方差
    println("training Mean Squared Error = " + MSE)
    println("模型的权重"+model.weights)
    println("模型的残差"+model.intercept)

    // Save and load model
    model.save(sc, "E:\\SparkCore2\\data\\mllib\\ridge-data\\scalaLinearRegressionWithSGDModel")
    val sameModel = LinearRegressionModel.load(sc, "E:\\SparkCore2\\data\\mllib\\ridge-data\\scalaLinearRegressionWithSGDModel")

    sc.stop()

    /**
      * The sample count：67
      * training Mean Squared Error = 7.4510328101026
      *模型的权重[1.440209460949548E-8,1.0686674736254139E-8,9.608973495307957E-9,4.553409983798095E-9,1.2221496560765207E-8,8.910773406981891E-9,5.5962085583952E-9,1.2255699128757168E-8]
      *模型的残差0.0
      */

  }
}

参考文献：

1andrew NG线性回归课件：链接：http://pan.baidu.com/s/1bTgHgq 密码：7mbt