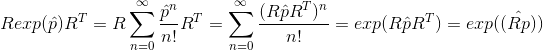- 高级编程--XML+socket练习题
masa010
java开发语言
1.北京华北2114.8万人上海华东2,500万人广州华南1292.68万人成都华西1417万人(1)使用dom4j将信息存入xml中(2)读取信息,并打印控制台(3)添加一个city节点与子节点(4)使用socketTCP协议编写服务端与客户端,客户端输入城市ID,服务器响应相应城市信息(5)使用socketTCP协议编写服务端与客户端,客户端要求用户输入city对象,服务端接收并使用dom4j
- C语言---程序设计练习题目及学习方法1
Wanyu677
C语言c语言学习方法算法
学习方法要多练习在这些题目中的代码和题目自己动手去敲练习也是在熟悉语法,写代码第一步就是熟悉语法练习是在锻炼编程思维,把实际问题转换为代码的能力学会画图画图去理解内存,理解指针这些比较难懂的知识画图可以更好的理清思路辅助理解,强化理解学会调试借助调试,更好的理解代码和感知代码找出代码中的bug和程序逻辑(1)自增自减运算符inta=5,b,c,i=10;b=a++;c=++b;printf("a=
- 创造价值很难?你只要帮别人节省时间!
破晓文库联盟
创造价值很难?你只要帮别人节省时间!我做教培行业的任课老师,已经有3年经验。我前一年都是在打磨自己的教学能力和演讲水平,脑袋里想的都是怎么让学生更容易理解这个知识点,更快地用习题巩固它。我用几个小时或者几节课帮学生节省了一周甚至一个月甚至半学期落下的知识点,我创造了价值,是因为我有总结归纳启发的能力。我用几节课帮家长节省了每天晚上每个周末对孩子的疯狂唠叨。你怎么还不去写作业?你作业写完了吗?为什么
- 三对角线型行列式的求法
Mr-Apple
笔记线性代数矩阵算法
三对角线型行列式摘要典型例题练习题参考答案摘要笔者在复习高等代数行列式这章时,发现三对角行列式问题是行列式计算中经常出现的一类行列式,部分考研院校也曾直接出过三对角行列式的计算,亦或是三对角行列式的变体问题.本文主要介绍了一种通常情况下三对角行列式的解法,即采用特征根法来求解行列式的通项公式.例1:计算nnn阶行列式(ac≠0)(ac\neq0)(ac=0)Dn=∣bc0…000abc…0000
- educoder实训平台python顺序结构答案_Educoder Python顺序结构习题
weixin_39710660
1.正方形与等腰三角形组成的多边形的面积square_length=4triangle_h=2.6area_square=4*4area_triangle=(2.6*4)/2area_total=area_square+area_triangleprint(area_total)2.平抛小球与抛出点的距离G=9.8v0=5t=2s=v0*th=(G*t**2)/2d=(s**2+h**2)**0.
- 笔记:Python顺序结构 练习题
辞言i
笔记python
文章目录前言一、什么是顺序结构?二、练习题1.题目2.填空题3.简答题4.编程题总结前言本次笔记旨在帮助读者加深对Python编程语言中顺序结构和选择题的理解。在学习Python编程过程中,掌握程序的基本结构以及条件语句的使用至关重要。通过本次练习题,读者将有机会测试自己对这些概念的掌握程度,并通过实际应用进一步巩固所学知识。本次练习题将涵盖Python中的顺序结构的练习题,旨在帮助读者提高解决问
- GPT-4-Turbo 和 Claude-3.5-Sonnet 图片识别出答题的是否正确 进行比较
光影3415
模型比较
1、比较的图片:====================使用GPT-4-Turbo输入的=============================提问:识别图片中的印刷字和手写字,如果写错的给一个正确答案+图片回复:在图片中,印刷字显示的是一系列的英语填空练习题,而手写字则是填入空白处的答案。以下是题目、选项、填入的答案,以及正确答案(如果填写错误)的列表:###印刷字内容与答案1.**Weput
- 信号与线性系统分析第4版吴大正课后习题答案
zgw100xuexi
考试信号与线性系统分析课后答案
完整版:http://zgw.100xuexi.com/SubItem/IndexInfoDetail.aspx?id=1d9ef631-a09d-4893-bb2f-597c745f5803第1章信号与系统1.1复习笔记本章是信号分析与系统分析的基础,详细介绍了信号与系统的概念与分类方法以及常用的连续信号与离散信号,讨论了冲激函数和冲激偶函数的重要性质,介绍了线性时不变(LTI)系统的特性,简要
- 可爱的学生
秋秋历史苑
上午,上完两节课后,本想在办公室休息一下,正遇上另一位老师临时有急事,她的一个学生交给我帮她管一下,很简单,也就是督促孩子记下词语,多音字以及练习题批改。二年级的一个小男孩,挺腼腆的。自己默默地在本子上记着七八个词语,过了一会儿,告诉我可以听写了。我接过孩子的书就开始了报词语。刚刚记忆了片刻,而且还抄写了几遍,居然合书即忘。其实大人也一样,一个生字,刚学会了它的读音及写法,呆会儿听写估计也得望。我
- 念旧人(一)
虫乐二
“我睡觉了,晚安,勿回。”“恩,晚安,勿回。”他将手机重新放在床头柜的抽屉里,每晚的信息聊天给沉闷压抑的高三增添了一丝不一样的色彩,她应该睡了吧,今天的作业那么多。“啊~~~”揉了揉惺忪的眼皮,伸了个懒腰舒服地打了个哈欠,他慢慢地走向了自己的床铺,往上一躺很快就进入了梦乡。高三的节奏是紧张而又充实的,永远都有需要巩固的知识点,永远都有需要背诵的重点,最重要的是永远都有做不完的习题。两人是怎么认识的
- java unix网络编程_《UNIX网络编程 卷2:进程间通信(第2版)》PDF 下载
weixin_39688019
javaunix网络编程
图书目录:第一部分简介第1章简介1.1概述1.2进程、线程与信息共享1.3IPC对象的持续性1.4名字空间1.5fork、exec和exit对IPC对象的影响1.6出错处理:包裹函数1.7Unix标准1.8书中IPC例子索引表1.9小结习题第2章PosixIPC2.1概述2.2IPC名字2.3创建与打开IPC通道2.4IPC权限2.5小结习题第3章SystemVIPC3.1概述3.2key_t键和
- Java语言程序设计与数据结构(基础篇)课后练习题 第十一章 (一)
2401_85111725
java数据结构python
publicStringtoString(){return"Triangle:side1="+s1+"side2="+s2+"side3="+s3;}}11.2=================================================================packagedishiyizhang;publicclassdishiyizhang{publicstati
- 【SWUST Online Judge】C语言《程序设计基础》作业一(1283、1284题)
保证安全,保证寿终正寝
科技c语言开发语言学习算法
〇、前言学姐纯粹是为爱发电,整理不易。所以小可爱们动动小手,点个免费的赞吧~以防找不到本文,收藏本文也完全不吃亏哟~一、题目列表链接指路:1.1283:输出语句练习2.1284:温度转换计算二、题目与题解(一)1283:输出语句练习题目描述在屏幕上输出以下信息:*******************欢迎使用小新通讯录[1]显示全部联系人[2]新增联系人[3]查找联系人[4]删除联系人[5]退出**
- C 习题
吃柠檬的鸮
练习1-12编写一个程序,以每行一个单词的形式打印其输出。/*ex12.c*/#include#defineIN1#defineOUT0intmain(){intc;intinword=OUT;while((c=getchar())!=EOF){if(c==''||c=='\n'||c=='\t'){if(inword){putchar('\n');inword=OUT;}}else{putcha
- 100道Python经典练习题.pdf(附答案)
IT娜娜
python开发语言后端程序人生数据分析
Python新手在谋求一份Python编程工作前,必须熟知Python的基础知识。编程网站DataFlair的技术团队分享了一份最常见Python面试题合集,既有基本的Python面试题,也有高阶版试题来指导你准备面试,试题均附有答案。面试题内容包括编码、数据结构、脚本撰写等话题。1:Python有哪些特点和优点?答:作为一门编程入门语言,Python主要有以下特点和优点:可解释具有动态特性面向对
- 第一章习题
2401_87136665
前端html5
1.网页标题为”网页学习“,在浏览器窗口中显示“欢迎大家一起开始学习网页制作”。代码及完成效果如下图所示。其中网页所以文字的颜色为blue,背景颜色为#99ffff;水平分割线粗细为5,颜色为#ff3333。网页学习body{background-color:#99ffff;color:blue;}hr{height:5px;background-color:#ff3333;border:none
- python入门学习
Krystal_kk
python学习记录python
最近开始学习python语言,看了一些视频,选择了《python编程:从入门到实践》这本书。看书跟着学,书前文推荐是每天看一章,但实际做下来,没课的时候一天可以看四章,上课的时候基本一上上半天,所以一天看两章问题不大。本来打算配合小甲鱼的python视频一起学习,但由于实在没时间所以放弃了。现在学到书的第七章,感觉还不错。分享一些我的学习笔记和这本书的一些课后习题答案给大家。为自己的学习生活也做一
- Unity基础之C#基础篇笔记5:变长参数和参数默认值,函数重载
四月的白羊座
unity基础之c#基础笔记
Unity基础之C#基础篇笔记5:变长参数和参数默认值,函数重载变长参数和参数默认值1.函数语法复习2.变长参数关键字3.参数默认值4.总结5.练习题函数重载1.基本概念2.实例3.总结4.习题变长参数和参数默认值1.函数语法复习1234static返回类型函数名(参数类型参数名1,参数类型参数名2,.......){函数的代码逻辑;函数的代码逻辑;函数的代码逻辑;.........;5retur
- 算法练习题24——查找杨辉三角中的组合数
mikey棒棒棒
算法数据结构java二分递推杨辉三角
题目描述杨辉三角中的每个元素是一个组合数。第(i)行的第(j)个元素表示组合数(C(i,j)),即从(i)个元素中选(j)个元素的组合方式。已知一个正整数(N),要求在杨辉三角中找到这个数,并输出它在杨辉三角中的具体位置。位置可以以第几行第几个元素的形式给出,或者将整个杨辉三角按顺序展开,输出(N)是展开后的第几个数。输入:一个整数(N)输出:输出整数(N)在杨辉三角中对应的位置,形式为:第几行的
- Java语言程序设计基础篇_编程练习题18.24 (将十六进制数转换为十进制数)
2301_78998594
第十八章-Java基础篇习题java开发语言学习
题目:18.24(将十六进制数转换为十进制数)编写一个递归方法,将一个字符串形式的十六进制数转换为一个十进制数。方法头如下:publicstaticinthex2Dec(StringhexString)编写一个测试程序,提示用户输入一个十六进制字符串,然后显示等价的十进制数。代码示例编程练习题18_24ConvertHexadecimalToDecimal.javapackagechapter_1
- 突破自己的枷锁
人生如梦001
过往的经历正在将我们固化,包括我们的长相、穿着、性格、行为、能力等等,在别人的眼中都成为一个特定的样子。从而,我们应该说什么话做什么事都有了别人眼中特定的模式。比如某人是老师和同学眼中的标准好学生,生性沉稳,学习努力,成绩优秀,从不参与跟学习无关的事情。那么跟学习相关的事情竞赛啊讲解习题啊,大家肯定都会去找他,但是嬉笑打闹等娱乐活动想必不是他应该干的事情。再比如公司的一个优秀员工,他工作勤勤恳恳,
- 算法设计与分析期末复习题汇总
wisdom_zhe
Java题库算法
文章目录1、选择题1.1选择题11.2选择题22、判断题2.1判断题12.2判断题23、填空题3.1算法填空3.2填空题24、简答题1、选择题1.1选择题11、下列不是动态规划算法基本步骤的是(A)。A、找出最优解的解空间B、构造最优解C、算出最优解D、定义最优解2、最大效益优先是(A)的一搜索方式。A、分支界限法B、动态规划法C、贪心法D、回溯法3、最长公共子序列算法利用的算法是(B)。A、分支
- 第六周工作总结
西凉燕衔妮
一、教学方面这周按计划上完了第四模块,三个班的进度还是不一样的,四年级的学生对于讲过的句型理解能力强,做起练习来也是很轻松的。现在主要是锻炼他们自主开口说话的能力,不管是读课文,还是讲题,他们都给人一种“不想说话”的感觉。所以在讲练习题的时候,我会让他们分析这道题,说出为什么是这个答案,目前看来,效果不错。五年级的整体学习氛围不错,但是有个不好的习惯就是上课老爱做小动作、说悄悄话。五年级本来女生就
- python核心编程课后习题答案--第一章
NewForMe
正则表达式1-1[bh][aiu]t;1-2\w+\w+;1-3\w+,\s\w+;1-4[A-Za-z_]+[\w_]+python有效标识符的定义:1.python中的标识符是区分大小写的。2.标示符以字母或下划线开头,可包括字母,下划线和数字。3.以下划线开头的标识符是有特殊意义的。1-5\d+(\s\w+)+1-6(1)^w{3}://.+com/?$(2)^\w+://.+?\.\w{3
- matlab simulink 过程控制,过程控制工程及仿真--基于MATLABSimulink.ppt
weixin_39721924
matlabsimulink过程控制
过程控制工程及仿真--基于MATLABSimulink《过程控制工程及仿真--基于MATLAB/Simulink》电子工业出版社出版2009.4作者:郭阳宽王正林联系邮箱:
[email protected]第5章PID控制5.1PID控制概述5.2PID控制算法5.3PID控制器参数整定5.4本章小结习题与思考内容提要本章描述PID控制的基本概念,介绍PID控制算法以及PID参数整定等基础知识,并通过
- 蒋辉【利他组】精进打卡2018.02.28
xiaohuihui620
蒋辉~咨询主管~利他组【日精进打卡第66天】【知~学习】《六项精进》2遍共134遍《大学》2遍共140遍【经典名句分享】一元复始万象更新【行~实践】一、修身:(对自己个人)1、做些小运动,锻炼身体。修身:(对帮扶对像)1、点饭。修身:(利他:给身边的同事做的善事)1、倒垃圾,一起吃饭二、齐家:(对家庭和家人)1、给弟弟买习题册。三、建功:(对工作)1、做咨询绩效表。{积善}:发愿从2017年12月
- 30道Python基础练习题
程序媛学姐
Pythonpython服务器开发语言
大家好,我是程序媛学姐,今天为大家梳理了30道Python基础练习题,方便大家学习参考。1.编写一个程序,输出"Hello,World!"这个程序的目标是简单地输出一条消息,即"Hello,World!"。在Python中,可以使用print语句来实现这个功能。示例代码:#输出"Hello,World!"print("Hello,World!")在上面的示例代码中,print("Hello,Wor
- 100 个 Python练习题[附代码]
宇宙大豹发
python算法java
需要更多python项目源码打包版本,领取方式在文末实例001:数字组合题目:有四个数字:1、2、3、4,能组成多少个互不相同且无重复数字的三位数?各是多少?程序分析:遍历全部可能,把有重复的剃掉。简便方法:用itertools中的permutations即可。importitertoolssum2=0a=[1,2,3,4]foriinitertools.permutations(a,3):pri
- 【操作系统原理】第六章课后习题
hiddenSharp429
计算机核心基础课程操作系统原理
前言课本:操作系统原理(第五版)[费翔林,骆斌编著]习题:主要习题内容是第一章到第六章,具体内容如下表章节内容链接第一章思考题1,3,7、应用题7,12(1)~(4)https://blog.csdn.net/Zchengjisihan/article/details/136493304?spm=1001.2014.3001.5501第二章思考题1,3,10,20,26,32,38,68、应用题7
- 计算机网络安装与调试题,计算机三级《网络技术》练习题及答案:无线局域网设备安装与调试...
曲陌柘凝
计算机网络安装与调试题
计算机三级《网络技术》练习题及答案:无线局域网设备安装与调试1[单选题]一个APRN覆盖的区域答为一个小区,一个小区的室内与室外覆盖范围分别是()A.30,150B.30,50C.30.500D.50.150参考答案:A2[单选题]某家庭需要通过无线局域网将分布在不同房间的三台计算机接入Internet,并且ISP只给其分配一个IP地址。在这种情况下,应该选用的设备是()A.APB.无线路由器C.
- ztree异步加载
3213213333332132
JavaScriptAjaxjsonWebztree
相信新手用ztree的时候,对异步加载会有些困惑,我开始的时候也是看了API花了些时间才搞定了异步加载,在这里分享给大家。
我后台代码生成的是json格式的数据,数据大家按各自的需求生成,这里只给出前端的代码。
设置setting,这里只关注async属性的配置
var setting = {
//异步加载配置
- thirft rpc 具体调用流程
BlueSkator
中间件rpcthrift
Thrift调用过程中,Thrift客户端和服务器之间主要用到传输层类、协议层类和处理类三个主要的核心类,这三个类的相互协作共同完成rpc的整个调用过程。在调用过程中将按照以下顺序进行协同工作:
(1) 将客户端程序调用的函数名和参数传递给协议层(TProtocol),协议
- 异或运算推导, 交换数据
dcj3sjt126com
PHP异或^
/*
* 5 0101
* 9 1010
*
* 5 ^ 5
* 0101
* 0101
* -----
* 0000
* 得出第一个规律: 相同的数进行异或, 结果是0
*
* 9 ^ 5 ^ 6
* 1010
* 0101
* ----
* 1111
*
* 1111
* 0110
* ----
* 1001
- 事件源对象
周华华
JavaScript
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/1999/xhtml&q
- MySql配置及相关命令
g21121
mysql
MySQL安装完毕后我们需要对它进行一些设置及性能优化,主要包括字符集设置,启动设置,连接优化,表优化,分区优化等等。
一 修改MySQL密码及用户
- [简单]poi删除excel 2007超链接
53873039oycg
Excel
采用解析sheet.xml方式删除超链接,缺点是要打开文件2次,代码如下:
public void removeExcel2007AllHyperLink(String filePath) throws Exception {
OPCPackage ocPkg = OPCPac
- Struts2添加 open flash chart
云端月影
准备以下开源项目:
1. Struts 2.1.6
2. Open Flash Chart 2 Version 2 Lug Wyrm Charmer (28th, July 2009)
3. jofc2,这东西不知道是没做好还是什么意思,好像和ofc2不怎么匹配,最好下源码,有什么问题直接改。
4. log4j
用eclipse新建动态网站,取名OFC2Demo,将Struts2 l
- spring包详解
aijuans
spring
下载的spring包中文件及各种包众多,在项目中往往只有部分是我们必须的,如果不清楚什么时候需要什么包的话,看看下面就知道了。 aspectj目录下是在Spring框架下使用aspectj的源代码和测试程序文件。Aspectj是java最早的提供AOP的应用框架。 dist 目录下是Spring 的发布包,关于发布包下面会详细进行说明。 docs&nb
- 网站推广之seo概念
antonyup_2006
算法Web应用服务器搜索引擎Google
持续开发一年多的b2c网站终于在08年10月23日上线了。作为开发人员的我在修改bug的同时,准备了解下网站的推广分析策略。
所谓网站推广,目的在于让尽可能多的潜在用户了解并访问网站,通过网站获得有关产品和服务等信息,为最终形成购买决策提供支持。
网站推广策略有很多,seo,email,adv
- 单例模式,sql注入,序列
百合不是茶
单例模式序列sql注入预编译
序列在前面写过有关的博客,也有过总结,但是今天在做一个JDBC操作数据库的相关内容时 需要使用序列创建一个自增长的字段 居然不会了,所以将序列写在本篇的前面
1,序列是一个保存数据连续的增长的一种方式;
序列的创建;
CREATE SEQUENCE seq_pro
2 INCREMENT BY 1 -- 每次加几个
3
- Mockito单元测试实例
bijian1013
单元测试mockito
Mockito单元测试实例:
public class SettingServiceTest {
private List<PersonDTO> personList = new ArrayList<PersonDTO>();
@InjectMocks
private SettingPojoService settin
- 精通Oracle10编程SQL(9)使用游标
bijian1013
oracle数据库plsql
/*
*使用游标
*/
--显示游标
--在显式游标中使用FETCH...INTO语句
DECLARE
CURSOR emp_cursor is
select ename,sal from emp where deptno=1;
v_ename emp.ename%TYPE;
v_sal emp.sal%TYPE;
begin
ope
- 【Java语言】动态代理
bit1129
java语言
JDK接口动态代理
JDK自带的动态代理通过动态的根据接口生成字节码(实现接口的一个具体类)的方式,为接口的实现类提供代理。被代理的对象和代理对象通过InvocationHandler建立关联
package com.tom;
import com.tom.model.User;
import com.tom.service.IUserService;
- Java通信之URL通信基础
白糖_
javajdkwebservice网络协议ITeye
java对网络通信以及提供了比较全面的jdk支持,java.net包能让程序员直接在程序中实现网络通信。
在技术日新月异的现在,我们能通过很多方式实现数据通信,比如webservice、url通信、socket通信等等,今天简单介绍下URL通信。
学习准备:建议首先学习java的IO基础知识
URL是统一资源定位器的简写,URL可以访问Internet和www,可以通过url
- 博弈Java讲义 - Java线程同步 (1)
boyitech
java多线程同步锁
在并发编程中经常会碰到多个执行线程共享资源的问题。例如多个线程同时读写文件,共用数据库连接,全局的计数器等。如果不处理好多线程之间的同步问题很容易引起状态不一致或者其他的错误。
同步不仅可以阻止一个线程看到对象处于不一致的状态,它还可以保证进入同步方法或者块的每个线程,都看到由同一锁保护的之前所有的修改结果。处理同步的关键就是要正确的识别临界条件(cri
- java-给定字符串,删除开始和结尾处的空格,并将中间的多个连续的空格合并成一个。
bylijinnan
java
public class DeleteExtraSpace {
/**
* 题目:给定字符串,删除开始和结尾处的空格,并将中间的多个连续的空格合并成一个。
* 方法1.用已有的String类的trim和replaceAll方法
* 方法2.全部用正则表达式,这个我不熟
* 方法3.“重新发明轮子”,从头遍历一次
*/
public static v
- An error has occurred.See the log file错误解决!
Kai_Ge
MyEclipse
今天早上打开MyEclipse时,自动关闭!弹出An error has occurred.See the log file错误提示!
很郁闷昨天启动和关闭还好着!!!打开几次依然报此错误,确定不是眼花了!
打开日志文件!找到当日错误文件内容:
--------------------------------------------------------------------------
- [矿业与工业]修建一个空间矿床开采站要多少钱?
comsci
地球上的钛金属矿藏已经接近枯竭...........
我们在冥王星的一颗卫星上面发现一些具有开采价值的矿床.....
那么,现在要编制一个预算,提交给财政部门..
- 解析Google Map Routes
dai_lm
google api
为了获得从A点到B点的路劲,经常会使用Google提供的API,例如
[url]
http://maps.googleapis.com/maps/api/directions/json?origin=40.7144,-74.0060&destination=47.6063,-122.3204&sensor=false
[/url]
从返回的结果上,大致可以了解应该怎么走,但
- SQL还有多少“理所应当”?
datamachine
sql
转贴存档,原帖地址:http://blog.chinaunix.net/uid-29242841-id-3968998.html、http://blog.chinaunix.net/uid-29242841-id-3971046.html!
------------------------------------华丽的分割线--------------------------------
- Yii使用Ajax验证时,如何设置某些字段不需要验证
dcj3sjt126com
Ajaxyii
经常像你注册页面,你可能非常希望只需要Ajax去验证用户名和Email,而不需要使用Ajax再去验证密码,默认如果你使用Yii 内置的ajax验证Form,例如:
$form=$this->beginWidget('CActiveForm', array( 'id'=>'usuario-form',&
- 使用git同步网站代码
dcj3sjt126com
crontabgit
转自:http://ued.ctrip.com/blog/?p=3646?tn=gongxinjun.com
管理一网站,最开始使用的虚拟空间,采用提供商支持的ftp上传网站文件,后换用vps,vps可以自己搭建ftp的,但是懒得搞,直接使用scp传输文件到服务器,现在需要更新文件到服务器,使用scp真的很烦。发现本人就职的公司,采用的git+rsync的方式来管理、同步代码,遂
- sql基本操作
蕃薯耀
sqlsql基本操作sql常用操作
sql基本操作
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
蕃薯耀 2015年6月1日 17:30:33 星期一
&
- Spring4+Hibernate4+Atomikos3.3多数据源事务管理
hanqunfeng
Hibernate4
Spring3+后不再对JTOM提供支持,所以可以改用Atomikos管理多数据源事务。Spring2.5+Hibernate3+JTOM参考:http://hanqunfeng.iteye.com/blog/1554251Atomikos官网网站:http://www.atomikos.com/ 一.pom.xml
<dependency>
<
- jquery中两个值得注意的方法one()和trigger()方法
jackyrong
trigger
在jquery中,有两个值得注意但容易忽视的方法,分别是one()方法和trigger()方法,这是从国内作者<<jquery权威指南》一书中看到不错的介绍
1) one方法
one方法的功能是让所选定的元素绑定一个仅触发一次的处理函数,格式为
one(type,${data},fn)
&nb
- 拿工资不仅仅是让你写代码的
lampcy
工作面试咨询
这是我对团队每个新进员工说的第一件事情。这句话的意思是,我并不关心你是如何快速完成任务的,哪怕代码很差,只要它像救生艇通气门一样管用就行。这句话也是我最喜欢的座右铭之一。
这个说法其实很合理:我们的工作是思考客户提出的问题,然后制定解决方案。思考第一,代码第二,公司请我们的最终目的不是写代码,而是想出解决方案。
话粗理不粗。
付你薪水不是让你来思考的,也不是让你来写代码的,你的目的是交付产品
- 架构师之对象操作----------对象的效率复制和判断是否全为空
nannan408
架构师
1.前言。
如题。
2.代码。
(1)对象的复制,比spring的beanCopier在大并发下效率要高,利用net.sf.cglib.beans.BeanCopier
Src src=new Src();
BeanCopier beanCopier = BeanCopier.create(Src.class, Des.class, false);
- ajax 被缓存的解决方案
Rainbow702
JavaScriptjqueryAjaxcache缓存
使用jquery的ajax来发送请求进行局部刷新画面,各位可能都做过。
今天碰到一个奇怪的现象,就是,同一个ajax请求,在chrome中,不论发送多少次,都可以发送至服务器端,而不会被缓存。但是,换成在IE下的时候,发现,同一个ajax请求,会发生被缓存的情况,只有第一次才会被发送至服务器端,之后的不会再被发送。郁闷。
解决方法如下:
① 直接使用 JQuery提供的 “cache”参数,
- 修改date.toLocaleString()的警告
tntxia
String
我们在写程序的时候,经常要查看时间,所以我们经常会用到date.toLocaleString(),但是date.toLocaleString()是一个过时 的API,代替的方法如下:
package com.tntxia.htmlmaker.util;
import java.text.SimpleDateFormat;
import java.util.
- 项目完成后的小总结
xiaomiya
js总结项目
项目完成了,突然想做个总结但是有点无从下手了。
做之前对于客户端给的接口很模式。然而定义好了格式要求就如此的愉快了。
先说说项目主要实现的功能吧
1,按键精灵
2,获取行情数据
3,各种input输入条件判断
4,发送数据(有json格式和string格式)
5,获取预警条件列表和预警结果列表,
6,排序,
7,预警结果分页获取
8,导出文件(excel,text等)
9,修
![]() ;
;![]() ,要证明这两个李群的积也还是李群,需要满足李群的两个条件:1.自反性:
,要证明这两个李群的积也还是李群,需要满足李群的两个条件:1.自反性:![]() ,2.行列式为1。实际上我们知道这就是在说正交矩阵中的旋转矩阵。但是这里还是再做一下证明。
,2.行列式为1。实际上我们知道这就是在说正交矩阵中的旋转矩阵。但是这里还是再做一下证明。![]()
![]() ,则同样:
,则同样:![]() ,从矩阵乘法维度我们知道
,从矩阵乘法维度我们知道![]() ,所以SE(3)乘法成群。
,所以SE(3)乘法成群。![]() ,
,,
![]() 构成李代数
构成李代数![]() 表示外积。我们可以假设任意
表示外积。我们可以假设任意![]() ,则要证明李代数需要证明其封闭性、双线性、自反性以及雅克比等价性。以下将会一一证明:
,则要证明李代数需要证明其封闭性、双线性、自反性以及雅克比等价性。以下将会一一证明:![]() ,
,![]() 。则:
。则:![]()
![]() 和
和![]() 满足李代数要求的性质。
满足李代数要求的性质。![]() ,按李括号运算为:
,按李括号运算为:![]()
![]() ,
,![]() 则根据双线性公式定义:
则根据双线性公式定义:![]() 。
。![]()
![]()
![]() ,
,![]() 。
。![]() ,则:
,则:![]()
,而
,
![]() 是一个单位向量,所以
是一个单位向量,所以![]() ,即
,即![]() 。
。![]() 展开:
展开:![]()
![]() 左乘一个旋转矩阵又右乘这个旋转矩阵的逆(旋转矩阵的逆等于矩阵的转置),右边是这个旋转矩阵乘以这个李代数,然后得到的三维向量取反对称矩阵。我们意识到,这两边最后的运算值是个矩阵。比较两个矩阵恒等有多中办法,比如比较矩阵中各个元素相等等等。矩阵表达的是一种投影关系,
左乘一个旋转矩阵又右乘这个旋转矩阵的逆(旋转矩阵的逆等于矩阵的转置),右边是这个旋转矩阵乘以这个李代数,然后得到的三维向量取反对称矩阵。我们意识到,这两边最后的运算值是个矩阵。比较两个矩阵恒等有多中办法,比如比较矩阵中各个元素相等等等。矩阵表达的是一种投影关系,![]() 中提取出来,明显没这种运算而且这种运算也是明显错误的也当做已知条件进行了证明。目前本人也没有特别好的证明方法,就用一种朴素(硬推)的方法验证我们之前的观察。
中提取出来,明显没这种运算而且这种运算也是明显错误的也当做已知条件进行了证明。目前本人也没有特别好的证明方法,就用一种朴素(硬推)的方法验证我们之前的观察。![]() ,则等式变为证明:
,则等式变为证明:![]()
![]() 提取出来,接下来的化简中我们将会用到旋转矩阵三向量正交的性质将式子再进一步化简。
提取出来,接下来的化简中我们将会用到旋转矩阵三向量正交的性质将式子再进一步化简。![]()
![]()
![]() 8.cmake的find_package指令是如何运作的?它有哪些可选参数?为了让cmake找到某个库,需要哪些先决条件?
8.cmake的find_package指令是如何运作的?它有哪些可选参数?为了让cmake找到某个库,需要哪些先决条件?
![\hat{\vec{a}}=\left [\begin{matrix} 0 & -a_{3} & a_{2}\\ a_{3} & 0 & -a_{1}\\ -a_{2} & a_{1} & 0 \end{matrix} \right ]](http://img.e-com-net.com/image/info8/0a47b4030d15426c894fcecb4b30210b.gif)
![R=\left [ \begin{matrix} \vec{r1} & \vec{r2} & \vec{r3} \end{matrix} \right ] \in \mathbb{R}^{3\times3},p=\left [ \begin{matrix} p_{1}\\ p_{2}\\ p_{3} \end{matrix} \right ]\in \mathbb{R}^{3}](http://img.e-com-net.com/image/info8/8840ecc8ed1243b1a5f39723d59d0136.gif)