决策树Decision Tree 和随机森林RandomForest基本概念（一）

一、决策树介绍

1.1 什么是决策树

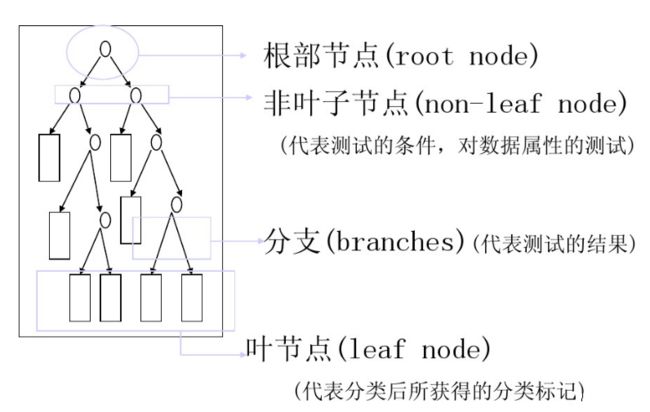
  类决策树模型是一种描述对实例进行分类的树形结构. 决策树由结点和有向边组成. 结点有两种类型: 内部结点和叶节点. 内部节点表示一个特征或属性, 叶节点表示一个类.
  决策树(Decision Tree),又称为判定树, 是一种以树结构(包括二叉树和多叉树)形式表达的预测分析模型.

• 通过把实例从根节点排列到某个叶子节点来分类实例
• 叶子节点为实例所属的分类
• 树上每个节点说明了对实例的某个属性的测试, 节点的每个后继分支对应于该属性的一个可能值

1.2 决策树种类

• 分类树–对离散变量做决策树
• 回归树–对连续变量做决策树

1.3 决策树学习过程

• 特征选择
• 决策树生成: 递归结构, 对应于模型的局部最优
• 决策树剪枝: 缩小树结构规模, 缓解过拟合, 对应于模型的全局选择

1.4 Entropy(熵)

  给定包含关于某个目标概念的正反样例的样例集S, 那么S相对这个布尔型分类的熵为:

  在信息论里面，信息熵衡量信息量的大小，也就是对随机变量不确定度的一个衡量。熵越大，不确定性越大；

1.5 information gain（信息增益）

  假设随机变量(X,Y), 其联合分布概率为P(X=xi,Y=yi)=Pij, i=1,2,…,n;j=1,2,…,m
  则条件熵H(Y|X)表示在已知随机变量X的条件下随机变量Y的不确定性, 其定义为X在给定条件下Y的条件概率分布的熵对X的数学期望

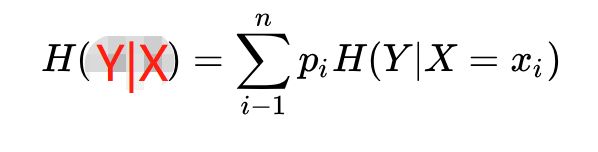
1.6 信息论

  若一事假有k种结果, 对应概率为P_i, 则此事件发生后所得到的信息量I为:

1.8 Gini系数

  Gini系数：

1.9 bagging method 和 random forests

  bagging method 和random forests 一般都是应用在决策树中。

• bagging method 的思想： 假设一个数据集L，通过Boostrap(自助抽样)有放回的抽样n次，那么产生了n个样本数据集，记为n个train集。
  1） 第一步：我们将这n个train集进行训练，因此产生了n个基分类器，也可以说是n个决策树
  2） 第二步：利用这n个基分类器对测试集进行预测，因此会得到n个结果。
  3） 第三步：采取多数投票（majorty vote）:将n个预测的结果出现频率最高的类作为总体预测。
• random forests 我们称为随机森林，其实随机森林是对装袋法的一种改进，随机森林也需要对自助抽样训练集建立一系列的决策树，这和决策树类似。
    随机森林在建立树的时候，不和装袋法一样，装袋法建树的时候是将所有预测变量都考虑进去，而随机森林则是考虑每一个分裂点时，都是从所有的预测变量p中随机选取m个预测变量，分裂点所用的预测变量只能从这m个变量中选择。在每个分裂点处都重新进行抽样，选出m个预测变量，通常m≈√p，对每一个分裂点来说，这个算法将大部分可用预测变量排除在外，虽然听起来crazy,但是这个原理是很巧妙的。
    其实当随机森林中的m=p时，随机森林和装袋法是一样的。随机森林考虑每个分裂点的子集相对来说比装袋法少很多。这样得到的树的平均值有更小的方差，因而树的可信度相对来说比较高。

1.10 剪枝算法

  决策树算法很容易过拟合（overfitting），剪枝算法就是用来防止决策树过拟合，提高泛华性能的方法。

  剪枝分为预剪枝与后剪枝

• 预剪枝是指在决策树的生成过程中，对每个节点在划分前先进行评估，若当前的划分不能带来泛化性能的提升，则停止划分，并将当前节点标记为叶节点。
• 后剪枝是指先从训练集生成一颗完整的决策树，然后自底向上对非叶节点进行考察，若将该节点对应的子树替换为叶节点，能带来泛化性能的提升，则将该子树替换为叶节点。

  那么怎么来判断是否带来泛化性能的提升那？

• 最简单的就是留出法，即预留一部分数据作为验证集来进行性能评估。

1.11 每个节点的位置如何确定？

  特征的选择：每次选入的特征作为分裂的标准，都是使得决策树在这个节点的根据你自己选择的标准（信息熵最小、信息增益最大、gini系数最小）.

1.12 每个节点在哪个值上做划分，确定分支结构呢？

  遍历划分的节点的分界值操作来解决这个问题

1.13 信息增益 vs 信息增益比

  之所以引入了信息增益比，是由于信息增益的一个缺点。那就是：信息增益总是偏向于选择取值较多的属性。信息增益比在此基础上增加了一个罚项，解决了这个问题。

1.13 Gini 指数 vs 熵

  既然这两个都可以表示数据的不确定性，不纯度。那么这两个有什么区别那？

• Gini 指数的计算不需要对数运算，更加高效；
• Gini 指数更偏向于连续属性，熵更偏向于离散属性。

二、决策树算法

  决策树学习的算法通常是一个递归地选择最优特征, 并根据该特征对训练数据进行分割, 使得各个子数据集有一个最好的分类的过程。

  在决策树算法中,ID3基于信息增益作为属性选择的度量, C4.5基于信息增益作为属性选择的度量, C5.0 是决策树C4.5的商用算法，在内存管理等方面，给出了改进。比如在商用软件SPSS中，就有该算法，CART基于基尼指数作为属性选择的度量。

2.0 决策树算法Hunt

  在Hunt算法中, 通过递归的方式建立决策树.

• 如果数据集D种所有的数据都属于一个类, 那么将该节点标记为节点。
• 如果数据集D中包含属于多个类的训练数据, 那么选择一个属性将训练数据划分为较小的子集, 对于测试条件的每个输出, 创建一个子节点, 并根据测试结果将D种的记录分布到子节点中, 然后对每一个子节点重复1,2过程, 对子节点的子节点依然是递归地调用该算法, 直至最后停止.

2.1 ID3

  ID3基于信息增益作为属性选择的度量，属性只能是枚举型的（离散的）,当然属性值可以是连续的数值型，但是需要对这些数据进行预处理，变为离散型的。

  熵表示的是数据中包含的信息量大小。熵越小，数据的纯度越高，也就是说数据越趋于一致，这是我们希望的划分之后每个子节点的样子。

  信息增益 = 划分前熵 - 划分后熵。信息增益越大，则意味着使用属性 a 来进行划分所获得的 “纯度提升” 越大 。也就是说，用属性 a 来划分训练集，得到的结果中纯度比较高。

  ID3 仅仅适用于二分类问题。ID3 仅仅能够处理离散属性。

ID3算法不足

• 使用ID3算法构建决策树时, 若出现各属性值取值数分布偏差大的情况, 分类精度会大打折扣
• ID3算法本身并未给出处理连续数据的方法
• ID3算法不能处理带有缺失值的数据集, 故在算法挖掘之前需要对数据集中的缺失值进行预处理
• ID3算法只有树的生成, 所以该算法生成的树容易产生过拟合

2.2 C4.5

  C4.5基于信息增益作为属性选择的度量，能够处理属性是连续型的。而且，在C4.5算法中，又提出了两个新的概念：

• 分离信息（Split Information）
• 信息增益率（Information gain ratio）

  C4.5 克服了 ID3 仅仅能够处理离散属性的问题，以及信息增益偏向选择取值较多特征的问题，使用信息增益比来选择特征。信息增益比 = 信息增益 / 划分前熵 ,选择信息增益比最大的作为最优特征。

  C4.5 处理连续特征是先将特征取值排序，以连续两个值中间值作为划分标准。尝试每一种划分，并计算修正后的信息增益，选择信息增益最大的分裂点作为该属性的分裂点。

2.2 C5.0

  C5.0 是决策树C4.5的商用算法，在内存管理等方面，给出了改进。比如在商用软件SPSS中，就有该算法。

2.3 CART

  注意: 上述三个算法只能做分类，不能做回归，下一篇博文CART类似于C4.5，但可以做回归。

  CART 的全称是分类与回归树。从这个名字中就应该知道，CART 既可以用于分类问题，也可以用于回归问题。

  CART基于基尼指数作为属性选择的度量.
  CART 与 ID3，C4.5 不同之处在于 CART 生成的树必须是二叉树。也就是说，无论是回归还是分类问题，无论特征是离散的还是连续的，无论属性取值有多个还是两个，内部节点只能根据属性值进行二分。

2.4 CART与ID3和C4.5的区别

• CART树是二叉树，而ID3和C4.5可以是多叉树
• CART在生成子树时，选择一个特征一个取值作为切分点，生成两个子树
• 选择特征和切分点的依据是Gini指数，选择Gini指数最小的特征及切分点生成子树

2.5 决策树与这些算法框架进行结合所得到的新的算法：

  Bagging + 决策树=随机森林
  Boosting + 决策树=提升树
  Gradient Boosting+决策树=GBDT总结

2.6 ID3,C4.5决策树的生成

  输入：训练集D，特征集A，阈值eps 输出：决策树

  若D中所有样本属于同一类Ck，则T为单节点树，将类Ck作为该节点的类标记，返回T

  若A为空集，即没有特征作为划分依据，则T为单节点树，并将D中实例数最大的类Ck作为该节点的类标记，返回T

  否则，计算A中各特征对D的信息增益（ID3）/信息增益比（C4.5）,选择信息增益最大的特征Ag

  若Ag的信息增益（比）小于阈值eps，则置T为单节点树，并将D中实例数最大的类Ck作为该节点的类标记，返回T

  否则，依照特征Ag将D划分为若干非空子集Di，将Di中实例数最大的类作为标记，构建子节点，由节点及其子节点构成树T，返回T

  对第i个子节点，以Di为训练集，以A-{Ag}为特征集，递归地调用1~5，得到子树Ti，返回Ti

三、决策树优缺点

3.1 优点

(1) 速度快: 计算量相对较小, 且容易转化成分类规则. 只要沿着树根向下一直走到叶, 沿途的分裂条件就能够唯一确定一条分类的谓词.
(2) 准确性高: 挖掘出来的分类规则准确性高, 便于理解, 决策树可以清晰的显示哪些字段比较重要, 即可以生成可以理解的规则.
(3) 可以处理连续和种类字段
(4) 不需要任何领域知识和参数假设
(5) 适合高维数据

3.2 缺点

(1) 对于各类别样本数量不一致的数据, 信息增益偏向于那些更多数值的特征
(2) 容易过拟合
(3) 忽略属性之间的相关性

四 随机森林基础概念

  

4.1 随机森林介绍

  随机森林就是通过集成学习的思想将多棵树集成的一种算法，它的基本单元是决策树，而它的本质属于机器学习的一大分支–集成学习（Ensemble Learning）方法。

  从直观角度来解释，每棵树都是一个分类器（假设现在为分类问题），那么对于一个输入样本，N棵树会有N个分类结果。而随机森林集成了所有的分类投票结果，将投票次数最多的类别指定为最终的输出，这就是一种最简单的Bagging思想。

4.2 随机森林的生成过程

• 从原始训练集中使用Bootstraping方法随机有放回采用选出m个样本，共进行n_tree次采样，生成n_tree个训练集
• 对于n_tree个训练集，分别训练n_tree个决策树模型
• 对于单个决策树模型，假设训练样本特征的个数为n，那么每次分裂时根据信息增益/信息增益比/Gini指数选择最好的特征进行分裂
• 每棵树都一直这样分裂下去，直到该节点的所有训练样例都属于同一类。在决策树的分裂过程中不需要剪枝
• 将生成的多棵决策树组成随机森林。对于分类问题，按多棵树分类器投票决定最终分类结果；对于回归问题，由多棵树预测的均值决定最终预测结果。

4.3 随机森林的评价指标–袋外误差（oob error）

  随机森林的关键问题是如何选择最优的m（特征个数），要解决这个问题主要依据袋外误差率oob error（out-of-bag error）

  随机森林一个重要的优点是，没有必要进行交叉验证或者用一个独立的测试集来获得误差的一个无偏估计。它可以在内部进行评估，也就是说在生成的过程中就可以对误差建立一个无偏估计。

  在构建每棵树时，对训练集使用了不同的bootstrap sample（随机有放回的抽取）。所以对每棵树而言（假设对第K棵树），大约有1/3的训练实例没有参与第K棵树的生成，它们成为第K棵树的oob样本。

oob估计的计算方法如下：

• 对每个样本，计算它作为oob样本的树对它的分类情况（约1/3的树）
• 然后以简单多数投票作为该样本的分类结果
• 最后用误分个数占样本总数的比率作为随机森林的oob误分率。

注意：oob误分率是随机森林泛化误差的一个无偏估计，它的结构近似于需要大量计算的k折交叉验证。

4.4 随机森林的特点

优点

• 在当前所有算法中，具有极高的准确率
• 随机性的引入，使得随机森林不容易过拟合
• 随机性的引入，使得随机森林有很好的抗噪声能力
• 能够有效的运行在大数据集上
  -能够评估各个特征在分类问题上的重要性
• 能够处理具有高维特征的输入样本，而不需要降维，并且不用做特征选择
• 既能处理离散型数据，也能处理连续型数据，数据集无需规范化
• 训练速度快，可以得到变量重要性排序
• 容易实现并行化
• 在生成过程中，能够获取到内部生成误差的一种无偏估计
• 对于缺省值问题也能够获得很好的结果

缺点

• 当随机森林中的决策树个数很多时，训练需要的空间和时间会较大
• 随机森林模型有许多不好解释的地方，算个黑盒模型

五、Bagging和Boosting的概念与区别

  随机森林属于集成学习（Ensemble Learning）中的bagging算法。在集成学习中，主要分为bagging算法和boosting算法。

5.1 Bagging算法（套袋法）：

Bagging的算法过程如下：

  从原始样本集中使用Bootstrap方法随机抽取n个训练样本，共进行k轮抽取，得到k个训练集。（k个训练集之间相互独立，元素可以有重复）
  对于k个训练集，我们训练k个模型（这个k个模型可以选择决策树，knn等）
  对于分类问题：由投票表决产生分类结构；对于回归问题：有k个模型预测结果的均值作为最后预测结构（所有模型的重要性相同）

5.2 Boosting（提升法）

boosting的算法过程如下：

  对于训练集的每个样本建立权值wi，增大被误分类的样本的权值
  进行迭代的过程中，每一步迭代都是一个弱分类器，需要用某种策略将其组合，作为最终模型。（例如AdaBoost给每个弱分类器一个权值，将其线性组合为最终分类器。误差越小的弱分类器，权值越大）

5.3 Bagging，Boosting的主要区别

• 样本选择上：Bagging采用的是Bootstrap随机有放回抽样；而Boosting每一轮的训练集是不变的，改变的只是每一个样本的权重。
• 样本权重：Bagging使用的是均匀取样，每个样本权重相等；Boosting根据错误率调整样本权重，错误率越大的样本权重越大。
• 预测函数：Bagging所有的预测函数的权重相等；Boosting中误差越小的预测函数（分类器）权重越大
• 并行计算：Bagging各个预测函数可以并行生成；Boosting各个预测函数（分类器）必须按照顺序迭代生成，就是不能并行计算

'''
【干货来了|小麦苗IT资料分享】
★小麦苗DB职场干货：https://mp.weixin.qq.com/s/Vm5PqNcDcITkOr9cQg6T7w
★小麦苗数据库健康检查：https://share.weiyun.com/5lb2U2M
★小麦苗微店：https://weidian.com/s/793741433?wfr=c&ifr=shopdetail
★各种操作系统下的数据库安装文件（Linux、Windows、AIX等）：链接：https://pan.baidu.com/s/19yJdUQhGz2hTgozb9ATdAw  提取码：4xpv
★小麦苗分享的资料：https://share.weiyun.com/57HUxNi
★小麦苗课堂资料：https://share.weiyun.com/5fAdN5m
★小麦苗课堂试听资料：https://share.weiyun.com/5HnQEuL
★小麦苗出版的相关书籍：https://share.weiyun.com/5sQBQpY
★小麦苗博客文章：https://share.weiyun.com/5ufi4Dx
★数据库系列（Oracle、MySQL、NoSQL）：https://share.weiyun.com/5n1u8gv
★公开课录像文件：https://share.weiyun.com/5yd7ukG
★其它常用软件分享：https://share.weiyun.com/53BlaHX
★其它IT资料（OS、网络、存储等）：https://share.weiyun.com/5Mn6ESi
★Python资料：https://share.weiyun.com/5iuQ2Fn
★已安装配置好的虚拟机：https://share.weiyun.com/5E8pxvT
★小麦苗腾讯课堂：https://lhr.ke.qq.com/
★小麦苗博客：http://blog.itpub.net/26736162/
'''

'''
有趣的事，Python永远不会缺席
欢迎关注小婷儿的博客

    文章内容来源于小婷儿的学习笔记，部分整理自网络，若有侵权或不当之处还请谅解

    如需转发，请注明出处：小婷儿的博客python    https://blog.csdn.net/u010986753

博客园 https://www.cnblogs.com/xxtalhr/

CSDN https://blog.csdn.net/u010986753

有问题请在博客下留言或加作者：
     微信：tinghai87605025 联系我加微信群
     QQ ：87605025
     python QQ交流群：py_data 483766429


培训说明
OCP培训说明连接 https://mp.weixin.qq.com/s/2cymJ4xiBPtTaHu16HkiuA

OCM培训说明连接 https://mp.weixin.qq.com/s/7-R6Cz8RcJKduVv6YlAxJA

     小婷儿的python正在成长中，其中还有很多不足之处，随着学习和工作的深入，会对以往的博客内容逐步改进和完善哒。重要的事多说几遍。。。。。。
'''

有趣的事，Python永远不会缺席

欢迎关注小婷儿的博客

  文章内容来源于小婷儿的学习笔记，部分整理自网络，若有侵权或不当之处还请谅解!!!

  如需转发，请注明出处：小婷儿的博客python    https://blog.csdn.net/u010986753

  CSDN https://blog.csdn.net/u010986753

  博客园 https://www.cnblogs.com/xxtalhr/

有问题请在博客下留言或加作者：
  微信：tinghai87605025 联系我加微信群
  QQ ：87605025
  QQ交流群：py_data 483766429
  公众号：DB宝

证书说明

  OCP证书说明连接 https://mp.weixin.qq.com/s/2cymJ4xiBPtTaHu16HkiuA

  OCM证书说明连接 https://mp.weixin.qq.com/s/7-R6Cz8RcJKduVv6YlAxJA

   小婷儿的python正在成长中，其中还有很多不足之处，随着学习和工作的深入，会对以往的博客内容逐步改进和完善哒。重要的事多说几遍。。。。。。