【算法笔记】图文结合彻底搞懂后缀数组

目录

1.后缀数组sa[]的求法O(nlogn)

2.rank数组的求法O(n)

3.height数组的求法O(n+)

---

可以先看文章末的参考博客！！

字符串：aabaaaab，读入时下标从0开始  

三个基本数组：

（1）sa[i]=j：第i名的后缀是[j,n)（i从1开始，j从0开始）

（2）rankk[i]=j：[i,n)的后缀排第j名（i从0开始，j从1开始）

（3）height[i]：排第i名的后缀和排第i-1名的后缀的最长公共前缀长度

1.后缀数组sa[]的求法O(nlogn)

---

倍增算法（基数排序） （还有一种比倍增算法更优的DC3算法，暂时不学）

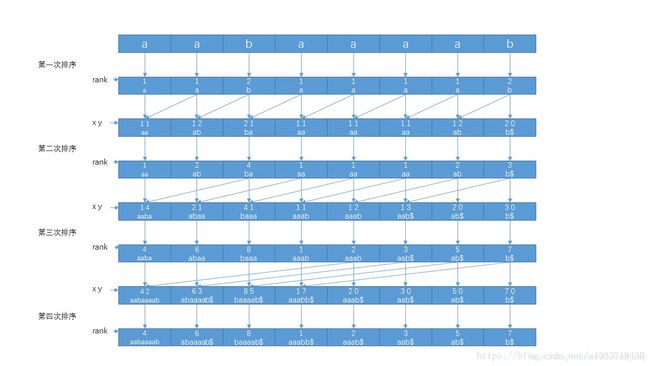
数组说明：

y[i] = j: 相当于第二关键字的sa数组，表示从下标j开始选取的第二关键字排第i名，同时y[i]也记录了字符串的开始下标，注意每次都把上一次排序处理的多个字符看成一个整体

x[i] =j :相当于第一关键字的rankk，表示从下标i开始的第一关键字排名为j

wv[i] = j：排名为i的第二关键字对应的第一关键字排名为j

（求前缀和的）wss[i] = j: 统计排名[0,i]区间所有排名出现的次数，处理的时候倒序处理

sa[i] = j: 表示从下标j开始选定的制定长度的字符字典序排名为i

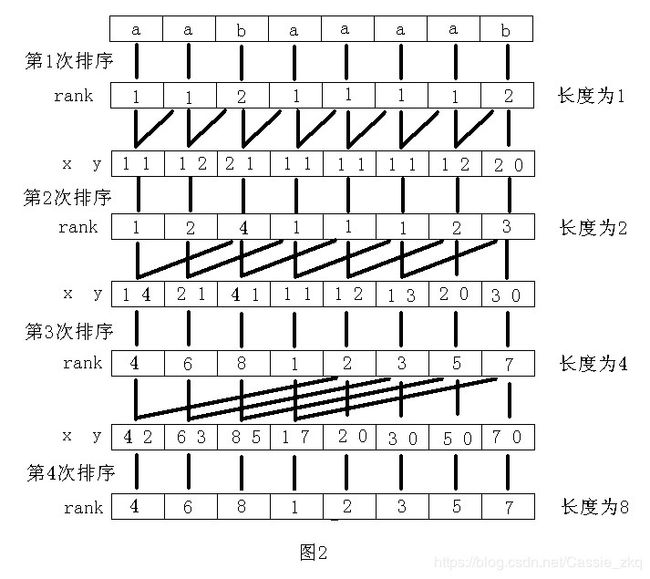
倍增算法求sa数组：

bool cmp(int *r, int a, int b, int l)
{
    return r[a] == r[b] && r[a + l] == r[b + l];
}
void get_sa(int *r, int *sa, int n, int m)
{
    int *x=wa, *y=wb;
    int p =0, i, j;
    for(i = 0; i < m; i++) wss[i] = 0;
    for(i = 0; i < n; i++) wss[ x[i]=r[i] ]++;
    for(i = 1; i <= m; i++) wss[i] += wss[i - 1];
    for(i = n - 1; i >= 0; i--) sa[--wss[x[i]]] = i;
    for(j = 1, p = 1; p < n; j *= 2, m = p)
    {
        //对第二关键字排序
        for(p = 0, i = n - j; i < n; i++) // [n-j,n)没有内容
            y[p++] = i;
        for(i = 0; i < n; i++)
            if(sa[i] >= j) y[p++] = sa[i] - j;
        //对字符串排序
        for(i = 0; i < n; i++) wv[i] = x[y[i]];
        for(i = 0; i < m; i++) wss[i] = 0;
        for(i = 0; i < n; i++) wss[wv[i]]++;
        for(i = 1; i <= m; i++) wss[i] += wss[i - 1];
        for(i = n - 1; i >= 0; i--) sa[--wss[wv[i]]] = y[i];
        //相同的字符串排名相同
        swap(x,y);
        for(i = 1, p = 1, x[sa[0]] = 0; i < n; i++)
            x[sa[i]] = cmp(y, sa[i-1], sa[i], j) ? p - 1 : p++;
    }
}

dc3算法求sa数组：（存个板子）O(n)，但是常数较大，又是也会超时 

const int max = 3*1e6+5
#define F(x) ((x)/3+((x)%3==1?0:tb))
#define G(x) ((x)=0;i--) b[--ws[wv[i]]]=a[i];
    return;
}
void dc3(int *r,int *sa,int n,int m)
{
    int i,j,*rn=r+n,*san=sa+n,ta=0,tb=(n+1)/3,tbc=0,p;
    r[n]=r[n+1]=0;
    for(i=0;i

模拟一遍倍增算法的程序基本上就懂个大概了。

---

对于字符串aabaaaab，长度是8，但是传入的参数n应该是8+1=9，把字符换成对应的int值，下面的代码执行的结果是：

    for(i = 0; i < m; i++) wss[i] = 0;
    for(i = 0; i < n; i++) wss[ x[i]=r[i] ]++;

i	0	1	2	3	4	5	6	7	8
r[i]	97	97	98	97	97	97	97	98	0
x[i]	97	97	98	97	97	97	97	98	0

i	0	1	.	.	96	97	98	99	.	.	.	255
wss[i]	1	0	0	0	0	6	2	0	0	0	0	0

---

 

    for(i = 1; i <= m; i++) wss[i] += wss[i - 1];

执行结果：求前缀和

 

i	0	1	2	.	.	96	97	98	99	.	.	255
wss[i]	1	1	1	1	1	1	7	9	9	9	9	9

---

 

    for(i = n - 1; i >= 0; i--) sa[--wss[x[i]]] = i;

执行结果：对单个字符进行初步排序，此时，对于相同的字符，先出现的排名高

i	0	1	2	3	4	5	6	7	8
下标为i的字符的排名	1	2	7	3	4	5	6	8	0

i	0	1	2	3	4	5	6	7	8
sa[i]	8	0	1	3	4	5	6	2	7

---

for循环内，执行倍增算法，先对第二关键字排序，所谓的第二关键字：当前字符（之后会是字符串，参考第一张图）后面j个字符。第一次j=1，那就是每个字符串后面1个字符就是第二关键字。对于aabaaaab的第二次排序的第二关键就是a、b、a、a、a、a、b、0（没有第二关键字后面补0⃣️)

        for(p = 0, i = n - j; i < n; i++) // [n-j,n)没有内容
            y[p++] = i;
        for(i = 0; i < n; i++)
            if(sa[i] >= j) y[p++] = sa[i] - j;

执行结果：这里的y数组是利用了上一次求出的sa[]，来获得第二关键字的大小关系，因为上一轮的字符串（已排好序）是这一轮的第一关键字，第一关键字已经有序，按照基数排序的思想，高位已经有序了，再考虑低位，优先排 排名高的高位对应的低位，所以i从0开始遍历，从排序高的第一关键字开始考虑它的第二关键字

i	0	1	2	3	4	5	6	7	8
y[i]	8	7	0	2	3	4	5	1	6

参考第二关键字验证正确性：

i	0	1	2	3	4	5	6	7	8	9
r[i]	97	97	98	97	97	97	97	98	0	0

---

 接下来对整个字符串排序：

for(i = 0; i < n; i++) wv[i] = x[y[i]];

执行结果：

i	0	1	2	3	4	5	6	7	8
wv[i]	0	98	97	98	97	97	97	97	97

---

        for(i = 0; i < m; i++) wss[i] = 0;
        for(i = 0; i < n; i++) wss[wv[i]]++;
        for(i = 1; i <= m; i++) wss[i] += wss[i - 1];

执行结果：

i	0	1	2	.	.	96	97	98	99	.	.	255
wss[i]	1	1	1	1	1	1	7	9	9	9	9	9

---

        for(i = n - 1; i >= 0; i--) sa[--wss[wv[i]]] = y[i];

 执行结果：参照字符串严重正确性，现在比较的是（每个后缀字符串的前两个字符）

i	0	1	2	3	4	5	6	7	8
sa[i]	8	0	3	4	5	1	6	7	2

---

x和y数组交换，此时因为可能有的字符串相同但是在对第一关键字排序后排名不同，要让相同的字符串的排名相同，用下面的代码实现：

        
bool cmp(int *r, int a, int b, int l)
{
    return r[a] == r[b] && r[a + l] == r[b + l];
}
swap(x,y);
for(i = 1, p = 1, x[sa[0]] = 0; i < n; i++)
    x[sa[i]] = cmp(y, sa[i-1], sa[i], j) ? p - 1 : p++;

执行结果：对比字符串可验证正确性，x[i]=j此时存的是：从下标j开始的前两个字符排名第i名，相当于rankk数组

i	0	1	2	3	4	5	6	7	8
x[i]	1	2	4	1	1	1	2	3	0

---

j=1*2，m=5

 //对第二关键字排序
        for(p = 0, i = n - j; i < n; i++) // [n-j,n)没有内容
            y[p++] = i;
        for(i = 0; i < n; i++)
            if(sa[i] >= j) y[p++] = sa[i] - j;

 执行结果：

i	0	1	2	3	4	5	6	7	8
y[i]	7	8	6	1	2	3	4	5	0

举例说明此时y[]的作用（手绘图），在原字符串的基础上：注意在上一轮排完序后已经把每个后缀的前两个字符看成了一个整体

y[2] =6表示在下标6+j-1后面（跳过下标6和下标7，从下标8开始）选择j个字符，这j个字符在这一轮的第二关键字中排第2名 

所以y数组相当于第二关键字的sa[]数组

 

---

通过rankk[sa[i]]=i得到排名第i的第二关键字对应的第一关键字的排名，wv[i]=m表示第二关键字排第i名，它的第一关键字排第m名

//排名为i的第二关键字对应的第一关键字的排名，x此时相当于rankk，y相当于第二关键字的sa
        for(i = 0; i < n; i++) wv[i] = x[y[i]]; 

执行结果：

i	0	1	2	3	4	5	6	7	8
wv[i]	3	0	2	2	4	1	1	1	1

---

        for(i = 0; i < m; i++) wss[i] = 0;
        for(i = 0; i < n; i++) wss[wv[i]]++;

执行结果：

i	0	1	2	3	4	5	...
wss[i]	1	4	2	1	1	0	0

---

        for(i = 1; i <= m; i++) wss[i] += wss[i - 1];

求前缀和： m = 5

i	1	2	3	4	5
wss[i]	5	7	8	9	9

---

y[i]相当于第二关键字的sa[i],第二关键字排第i名，它的第一关键字排第wv[i]名，y[i]记录了这四个字符的开始下标

        for(i = n - 1; i >= 0; i--) sa[--wss[wv[i]]] = y[i];

执行结果：

i	0	1	2	3	4	5	6	7	8
sa[i]	8	3	4	5	0	6	1	7	2

---

再让相同的字符排序相同 

        swap(x,y);
        for(i = 1, p = 1, x[sa[0]] = 0; i < n; i++)
            x[sa[i]] = cmp(y, sa[i-1], sa[i], j) ? p - 1 : p++;

至此，p=9 >8，说明给定的aabaaaab的8个后缀字符串已经排好序了，结束循环，最终求得sa数组，x数组相当于rankk数组 

总结：搞懂下面这几个数组很重要！！我没有在网上找到有具体讲解下面的数组的博客！(◎_◎;)

r[]:存输出的字符串对应的int值

y[i] = j: 相当于第二关键字的sa数组，表示从下标j开始选取的第二关键字排第i名，同时y[i]也记录了字符串的开始下标，注意每次都把上一次排序处理的多个字符看成一个整体

x[i] =j :相当于第一关键字的rankk，表示从下标i开始的第一关键字排名为j

wv[i] = j：排名为i的第二关键字对应的第一关键字排名为j

（求前缀和的）wss[i] = j: 统计排名[0,i]区间所有排名出现的次数，处理的时候倒序处理

sa[i] = j: 表示从下标j开始选定的制定长度的字符字典序排名为i

在每一轮求得sa数组之后，x记录此轮的rankk值，并让相同的字符串排名相同，最终处理到排名值超过字符串长度结束。

最终求得的排名从1开始才有意义，字符串下标仍是从0开始的。

 

2.rank数组的求法O(n)

---

性质：rankk[sa[i]]=i, sa[rankk[i]]=i

    for(int i = 1; i <= n; i++) rankk[sa[i]] = i;

 

3.height数组的求法O(n+)

---

(文字来源https://blog.csdn.net/wangushang2/article/details/7827873)

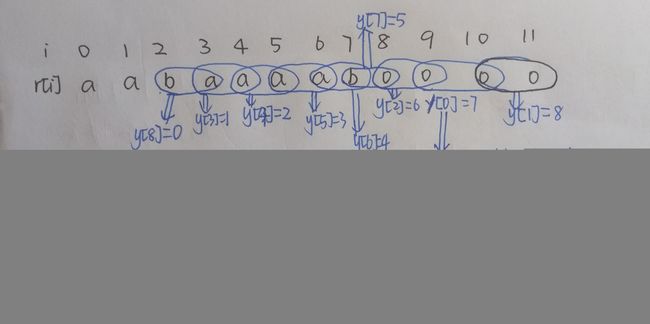
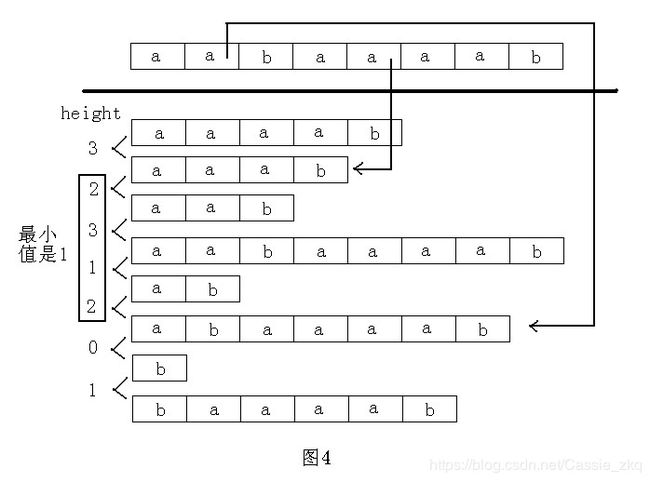
height数组：定义height[i]=suffix(sa[i-1])和suffix(sa[i])的最长公共前缀，也就是排名相邻的两个后缀的最长公共前缀。那么对于j和k，不妨设rank[j]

suffix(j)和suffix(k)的最长公共前缀为height[rank[j]+1]，height[rank[j]+2]，height[rank[j]+3]，……，height[rank[k]]中的最小值。

例如，字符串为“aabaaaab”，求后缀“abaaaab”和后缀“aaab”的最长公共前缀，如图4所示：

 

 

那么应该如何高效的求出height值呢？

如果按height[2]，height[3]，……，height[n]的顺序计算，最坏情况下时间复杂度为O(n2)。这样做并没有利用字符串的性质。定义h[i]=height[rank[i]]，也就是suffix(i)和在它前一名的后缀的最长公共前缀。

h数组有以下性质：

h[i]≥h[i-1]-1

证明：

设suffix(k)是排在suffix(i-1)前一名的后缀，则它们的最长公共前缀是h[i-1]。那么suffix(k+1)将排在suffix(i)的前面（这里要求h[i-1]>1，如果h[i-1]≤1，原式显然成立）并且suffix(k+1)和suffix(i)的最长公共前缀是h[i-1]-1，所以suffix(i)和在它前一名的后缀的最长公共前缀至少是h[i-1]-1。按照h[1]，h[2]，……，h[n]的顺序计算，并利用h数组的性质，时间复杂度可以降为O(n)。

实现代码：

注意for中i的下标是从0开始的，以为字符串的下标是从0开始的，所以定存在rankk[0]，否则就错了

小心后缀数组里的for循环左右边界！

void get_height(int n)
{
    int k = 0;
    for(int i = 0; i < n; i++)
    {
        k ? k-- : 0;//根据性质height[rank[i]] ≥ (height[rank[i-1]] -1)
        int j = sa[rankk[i] - 1];//上一名的开始下标
        while(r[i + k] == r[j + k]) k++;
        height[rankk[i]] = k;
    }
}

【参考博客】：

https://www.cnblogs.com/shanchuan04/p/5324009.html

https://blog.csdn.net/wangushang2/article/details/7827873

https://blog.csdn.net/a1035719430/article/details/80217267