图解概率论基础概念(条件概率、全概率公式、贝叶斯公式)
利用一个例子来讲解以下概率论的基础概念:
- 条件概率
- 联合概率
- 全概率公式
- 贝叶斯公式
小英是一名跑步爱好者,下面统计了小英100天的跑步情况,这100天有不同的天气情况,小英也不是每天都跑步。下面结合例子开始介绍概率论的基础概念。
概率
概率表示某事件发生的可能性
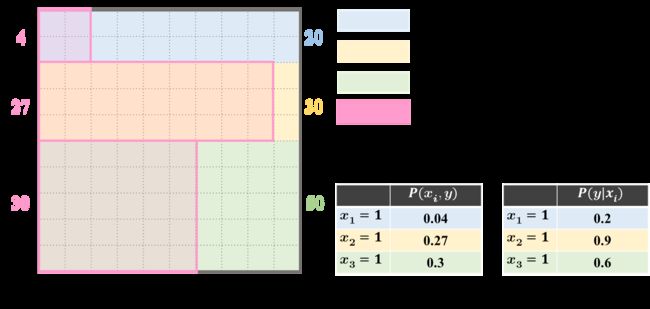
图1一共有100个格子,格子里的颜色表示一天的天气状况,共有100天。其中有20天下雨(蓝色),30天刮风(黄色),50天晴天(绿色)。那么数格子很容易可以算出某天天气是下雨或刮风或晴天的概率:
- P ( x 1 = 1 ) = 20 / 100 = 0.2 P(x_1=1)=20/100=0.2 P(x1=1)=20/100=0.2,表示某天是小雨的概率,简写为 P ( x 1 ) = 0.2 P(x_1)=0.2 P(x1)=0.2
- P ( x 2 ) = 0.3 P(x_2)=0.3 P(x2)=0.3
- P ( x 3 ) = 0.5 P(x_3)=0.5 P(x3)=0.5
由此得到表1。
联合概率
联合概率表示多事件同时发生的概率
先来看图2,粉色格子表示在这天小英跑步了,从图中可以数出:小雨时小英有4天在跑步;刮风时小英跑了27天;晴天小英有30天在跑步。很容易数出,小英在下雨天且跑步的概率就是 P ( x 1 = 1 , y = 1 ) = 4 / 100 = 0.04 P(x_1=1,y=1)=4/100=0.04 P(x1=1,y=1)=4/100=0.04简写为 P ( x 1 , y ) P(x_1,y) P(x1,y),用逗号隔开表示两件事同时发生的概率。
- P ( x 1 , y ) = 0.04 P(x_1,y)=0.04 P(x1,y)=0.04
- P ( x 2 , y ) = 0.27 P(x_2,y)=0.27 P(x2,y)=0.27
- P ( x 3 , y ) = 0.3 P(x_3,y)=0.3 P(x3,y)=0.3
由此得到表2
条件概率
条件概率表示,在某事发生的前提之下,另一件事发生的概率。
比如计算:下雨时,小英跑步的概率。一共有20个蓝色格子,表示下了20天雨,其中有4个是被粉色格子覆盖的。则下雨天,小英跑步的概率就是 P ( y = 1 ∣ x 1 = 1 ) = 4 / 20 = 0.2 P(y=1|x_1=1)=4/20=0.2 P(y=1∣x1=1)=4/20=0.2,简写为 P ( y ∣ x 1 ) = 0.2 P(y|x_1)=0.2 P(y∣x1)=0.2,则:
- P ( y ∣ x 1 ) = 0.2 P(y|x_1)=0.2 P(y∣x1)=0.2
- P ( y ∣ x 2 ) = 0.9 P(y|x_2)=0.9 P(y∣x2)=0.9
- P ( y ∣ x 3 ) = 0.6 P(y|x_3)=0.6 P(y∣x3)=0.6
由此得到表3。
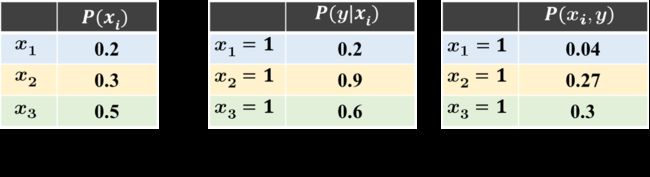
把表1、2、3摆在一起可以看出(注意换了位置),表2其实就是表1和表3对应元素相乘。
这就引出了联合概率公式:
P ( x i , y ) = P ( x i ) P ( y ∣ x i ) (1) P(x_i,y)=P(x_i)P(y|x_i) \tag{1} P(xi,y)=P(xi)P(y∣xi)(1)
变换一下次序就是条件概率公式:
P ( y ∣ x i ) = P ( x i , y ) P ( x i ) (2) P(y|x_i)=\frac{P(x_i,y)}{P(x_i)} \tag{2} P(y∣xi)=P(xi)P(xi,y)(2)
注:更一般化的公式应该是联合概率 P ( A , B ) = P ( A ) P ( B ∣ A ) P(A,B)=P(A)P(B|A) P(A,B)=P(A)P(B∣A)和条件概率 P ( B ∣ A ) = P ( A , B ) / P ( A ) P(B|A)=P(A,B)/P(A) P(B∣A)=P(A,B)/P(A),其实就是符号的区别。这里边A和B填任何符号都行。
全概率公式
根据表1,表2,表3怎么计算小英在某天跑步的概率?
如果看着图数粉色格子的话,很容易得出 P ( y = 1 ) = ( 4 + 27 + 30 ) / 100 = 0.61 P(y=1)=(4+27+30)/100=0.61 P(y=1)=(4+27+30)/100=0.61。简写为 P ( y ) = 0.61 P(y)=0.61 P(y)=0.61。
把这个公式拆解一下可以得到下面这样的计算式:
P ( y ) = 4 100 + 27 100 + 30 100 = 20 100 4 20 + 30 100 27 30 + 50 100 30 50 = 0.2 ⋅ 0.2 + 0.3 ⋅ 0.9 + 0.5 ⋅ 0.6 \begin{aligned} P(y)&=\frac{4}{100}+\frac{27}{100}+\frac{30}{100}\\ &=\frac{20}{100}\frac{4}{20}+\frac{30}{100}\frac{27}{30}+\frac{50}{100}\frac{30}{50}\\ &=0.2 \cdot0.2+0.3\cdot0.9+0.5\cdot0.6 \end{aligned} P(y)=1004+10027+10030=10020204+100303027+100505030=0.2⋅0.2+0.3⋅0.9+0.5⋅0.6
可以看到公式的最后一行实际上就是表1和表3对应元素相乘再相加。
把这个过程写成公式就是:
P ( y ) = P ( x 1 ) P ( y ∣ x 1 ) + P ( x 2 ) P ( y ∣ x 2 ) + P ( x 3 ) P ( y ∣ x 3 ) = ∑ i = 1 n P ( x i ) P ( y ∣ x i ) \begin{aligned} P(y)&=P(x_1)P(y|x_1) + P(x_2)P(y|x_2) + P(x_3)P(y|x_3)\\ &=\sum_{i=1}^{n}P(x_i)P(y|x_i) \end{aligned} P(y)=P(x1)P(y∣x1)+P(x2)P(y∣x2)+P(x3)P(y∣x3)=i=1∑nP(xi)P(y∣xi)
这个例子里 n = 3 n=3 n=3。
全概率公式为:
P ( y ) = ∑ i = 1 n P ( x i ) P ( y ∣ x i ) (3) P(y)=\sum_{i=1}^{n}P(x_i)P(y|x_i) \tag{3} P(y)=i=1∑nP(xi)P(y∣xi)(3)
为何不直接用表2和公式 P ( x i , y ) P(x_i,y) P(xi,y)?
很多时候我们从题目得不到联合概率 P ( x i , y ) P(x_i,y) P(xi,y)的信息,一般都能得到某变量发生的概率 P ( x i ) P(x_i) P(xi)或条件概率 P ( y ∣ x i ) P(y|x_i) P(y∣xi),反正 P ( x i ) P ( y ∣ x i ) P(x_i)P(y|x_i) P(xi)P(y∣xi)也能表示 P ( x i , y ) P(x_i,y) P(xi,y),那不如用适用性更广的公式。
结合图2和图3来看,全概率公式其实就是一个分而治之的思想,每种天气状态都会对应不同的小英跑步的概率,而天气状态的概率又各不相同。这两个概率相乘再相加就得到了小英跑步的概率。
贝叶斯公式
之前我们都是在100天的范围之下讨论小英跑步的问题的
现在把讨论范围缩小:在小英跑步的日子中,下雨的天数是多少?
把表示跑步的粉色部分从图2扣下来就形成了图4。
这个问题的答案数一下便知 P ( x 1 ∣ y ) = 4 / ( 4 + 27 + 30 ) = 4 / 61 P(x_1|y)=4/(4+27+30)=4/61 P(x1∣y)=4/(4+27+30)=4/61
稍微推导一下,根据之前得到的条件概率公式(2)可得
P ( x i ∣ y ) = P ( x i , y ) P ( y ) P(x_i|y)=\frac{P(x_i,y)}{P(y)} P(xi∣y)=P(y)P(xi,y)
再根据联合概率公式(1)和全概率公式(3)可得贝叶斯公式:
P ( x i ∣ y ) = P ( x i ) P ( y ∣ x i ) ∑ j = 1 n P ( x j ) P ( y ∣ x j ) (4) P(x_i|y)=\frac{P(x_i)P(y|x_i)}{\sum_{j=1}^nP(x_j)P(y|x_j)} \tag{4} P(xi∣y)=∑j=1nP(xj)P(y∣xj)P(xi)P(y∣xi)(4)
把 x 1 x_1 x1带入贝叶斯公式(4)就有:
P ( x 1 ∣ y ) = P ( x 1 ) P ( y ∣ x 1 ) ∑ j = 1 n P ( x j ) P ( y ∣ x j ) = P ( x 1 ) P ( y ∣ x 1 ) P ( x 1 ) P ( y ∣ x 1 ) + P ( x 2 ) P ( y ∣ x 2 ) + P ( x 3 ) P ( y ∣ x 3 ) = 0.2 ⋅ 0.2 0.2 ⋅ 0.2 + 0.3 ⋅ 0.9 + 0.6 ⋅ 0.5 = 0.04 0.61 = 4 61 \begin{aligned} P(x_1|y)&=\frac{P(x_1)P(y|x_1)}{\sum_{j=1}^nP(x_j)P(y|x_j)}\\ &=\frac{P(x_1)P(y|x_1)}{P(x_1)P(y|x_1)+P(x_2)P(y|x_2)+P(x_3)P(y|x_3)}\\ &=\frac{0.2\cdot0.2}{0.2\cdot0.2+0.3\cdot0.9+0.6\cdot0.5}\\ &=\frac{0.04}{0.61}\\ &=\frac{4}{61} \end{aligned} P(x1∣y)=∑j=1nP(xj)P(y∣xj)P(x1)P(y∣x1)=P(x1)P(y∣x1)+P(x2)P(y∣x2)+P(x3)P(y∣x3)P(x1)P(y∣x1)=0.2⋅0.2+0.3⋅0.9+0.6⋅0.50.2⋅0.2=0.610.04=614
其实核心思想就是把条件概率公式拆分得更细了,理论是很简单的。推导过程可能看起来有点复杂,结合图4看就很清晰了。 P ( x 1 ∣ y ) P(x_1|y) P(x1∣y)的分子就是一个联合概率公式,下部分就是全概率公式。只要式(1)(2)(3)都掌握好了,贝叶斯公式就很简单。
P ( x 1 ∣ y ) = 联 合 概 率 全 概 率 P(x_1|y)=\frac{联合概率}{全概率} P(x1∣y)=全概率联合概率
- P ( x 1 ∣ y ) = 4 / 61 P(x_1|y)=4/61 P(x1∣y)=4/61
- P ( x 2 ∣ y ) = 27 / 61 P(x_2|y)=27/61 P(x2∣y)=27/61
- P ( x 3 ∣ y ) = 30 / 61 P(x_3|y)=30/61 P(x3∣y)=30/61
可以把贝叶斯概率公式理解为范围缩小了的概率问题。