算法设计与分析- Stable Matching-Gale_Shapley

一. 算法引导

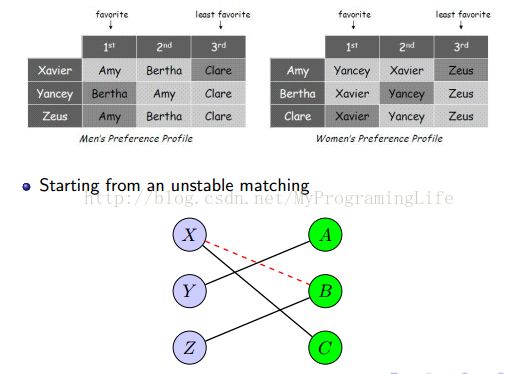
稳定匹配算法， 在平常相亲活动中，有 n 男, n 女， 这时进行相亲活动，就要根据喜好进行优先顺序的排列，每个人都有自己的喜好，因此，这就有最终的匹配是否稳定那，两个人稳定的匹配结婚才会有结果。

举个栗子：

对于这样的结果那，X 喜欢 B 胜于喜欢 C， 同时 B 喜欢 X 胜于喜欢 Z ， 这样就会出现不稳定的情况， 应该考虑 X-B 的匹配情况。

二. 算法实现

描述： 有 1 到 M 个 Man, 和 1 到 W 个Woman, 然后这时每个男孩和女孩对对方都有一个排序， 我们找出没有匹配的男性，对其进行讨论， 他的排序表中，从高到低进行匹配，如果 挑选的这个 W且还没匹配过，其巧好没有匹配，则他俩 匹配， 若匹配了，则看W 匹配的 M‘ 的 高低顺序 与 M 的高低顺序（这里的高低顺序是在W 眼中的高低顺序）， 如果M高，则替换掉M’, 使其恢复单身， 否则， 就在此中再任意找一个没匹配的男性。

这里有个ppt， 描述的很详细，过程完全是一看即懂！每个人都有自己的喜好吗，哈哈。 http://download.csdn.net/detail/myprograminglife/8349497

编程实现：

首先获得一个每个人的排序表男女排序文件：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

using namespace std;

vector gen_boys(int number)
{
    vector result;
    for(int i = 0; i < number; i++){
        string boy = "B";
        string s;
        stringstream ss;
        ss << i;
        ss >> s;
        boy.append(s);
        result.push_back(boy);
    }
    return result;
}

vector gen_girls(int number)
{
    vector result;
    for(int i = 0; i < number; i++){
        string boy = "G";
        string s;
        stringstream ss;
        ss << i;
        ss >> s;
        boy.append(s);
        result.push_back(boy);
    }
    return result;
}

vector gen_ranking(vector candidate)
{
    random_shuffle(candidate.begin(), candidate.end());
    return candidate;
}

void write_rankings(vector people, vector > rankings, string out_file)
{
    ofstream ofs(out_file.c_str());
    if(ofs.fail()){
        cerr << "Error: " << out_file << endl;
        return;
    }
    for(int i = 0; i < people.size(); i++){
        ofs << people[i] << ":";
        for(int j = 0; j < rankings[i].size(); j++){
            ofs << " " << rankings.at(i).at(j);
        }
        ofs << endl;
    }
    ofs.close();
}

int main(int argc, char ** argv)
{
    srand(time(NULL));
    int n = 200;
    vector boys = gen_boys(n);
    vector girls = gen_girls(n);
    vector > boys_rankings;
    vector > girls_rankings;
    for(int i = 0; i < n; i++){
        boys_rankings.push_back(gen_ranking(girls));
        girls_rankings.push_back(gen_ranking(boys));
    }
    write_rankings(boys, boys_rankings, "boys_rankings.txt");
    write_rankings(girls, girls_rankings, "girls_rankings.txt");
    return 1;
}

然后实现上述伪代码;

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

using namespace std;

// 该头文件，用来将string数据 转化为int 这样进行匹配。
//boys 是矩阵  girls 是矩阵
vector GaleShapley(vector > boys, vector > girls, int number)
{
	vector boy_partner(number);
	vector girl_partner(number);
	vector boy_partner_bool(number);    //标记看看是否为单身状态0-单身， 1-有伴
	vector girl_partner_bool(number);
	vector boy_index_account(number);   //用于检索boy 已经向几个女生求过婚了
	
	bool loop = true;
	int count_dead = 0;
	int new_boy_index;
	int in_boy_count_index;
	int new_girl_index;
	int old_boy_position = 0;

		for (int iter_index = 0; iter_index < number; ++iter_index)
	{
		boy_partner_bool[iter_index] = 0;
		girl_partner_bool[iter_index] = 0;
		boy_index_account[iter_index] = 0;
	}
	while (loop)
	{
		// 如果全部boyPartnerbool[m] = 1，退出循环。
		for (new_boy_index = 0; new_boy_index < number; new_boy_index++)
		{
			if (boy_partner_bool[new_boy_index] == 0)				 //单身男孩
			{
				in_boy_count_index = boy_index_account[new_boy_index];         //单身男孩求婚的对象
				boy_index_account[new_boy_index] += 1;						 //单身男孩求婚对象的更新
				new_girl_index = boys[new_boy_index][in_boy_count_index];  //单身男孩向此女孩求婚
				if (girl_partner_bool[new_girl_index] == 0)          //if - 被求婚女孩也单身        
				{
					boy_partner[new_boy_index] = new_girl_index;      //两个成为对象
					girl_partner[new_girl_index] = new_boy_index; 
					
					boy_partner_bool[new_boy_index] = 1;             //两人告别单身
					girl_partner_bool[new_girl_index] = 1;
					count_dead += 1; 
				}  //end girl 单身
				else                                             //else - 别求婚女孩有对象
				{	
					for (int find_girl_old_position = 0; find_girl_old_position < number; find_girl_old_position++)
						if (girls[new_girl_index][find_girl_old_position] == girl_partner[new_girl_index])
							old_boy_position = find_girl_old_position;
					//vector::const_iterator oldBoyPosition = find(girls[newGirlIndex].begin() , girls[newGirlIndex].end() , girlPartner[newGirlIndex]);
					//for (vector::const_iterator iterNewGirlPrefer = girls[newGirlIndex].begin(); iterNewGirlPrefer != oldBoyPosition; ++iterNewGirlPrefer)
					for (int is_new_boy_prefer = 0; is_new_boy_prefer < old_boy_position; is_new_boy_prefer++)
					{ 

						if (girls[new_girl_index][is_new_boy_prefer] == new_boy_index)       // 被求婚女孩有对象，更喜欢新男孩
						{
							int oldGirlPartner = girl_partner[new_girl_index];
							boy_partner_bool[oldGirlPartner] = 0;       //旧男孩又恢复单身状态
							
							boy_partner[new_boy_index] = new_girl_index;      //两个成为对象
					        girl_partner[new_girl_index] = new_boy_index; 

							boy_partner_bool[new_boy_index] = 1;          //新男孩厉害找到对象
						}
					} // end
				}  //end else女孩有对象
				break;
			}   //end if 有单身
			else if (count_dead == number)             //结束的标志,没有男孩单身
			{
				loop = false;
				break;
			} //end else 
		} //end for newBoyIndex
	} //end while
	return boy_partner;
}

void ObtainRinkings(vector > &rankings, string in_file, int row_number)
{
	
	vector ranking;
	vector peoples;
	string each_rangking;
	string people;
	ifstream ifs;

	ifs.open(in_file);
	if (!ifs.is_open())
	{
		cout << "Could not open the file" << in_file << endl;
		exit(EXIT_FAILURE);
	}
	
	for(int row = 0; row < row_number; row++)
	{
		ifs >> people;
		peoples.push_back(people);
		while(ifs.get() != '\n')
		{
			ifs>>each_rangking;
			ranking.push_back(each_rangking);
		}
		rankings.push_back(ranking);
		ranking.clear();
	}
	ifs.close();
}

void NumberRanking(vector > &rangkings, vector > &number_rankings)
{
	vector one_body;
	int rank;
	int ranking_number_count;

	for (int row = 0; row < rangkings.size(); row++)
	{
		for (int col = 0; col < rangkings.size(); col++)
		{

			stringstream ss;
			ranking_number_count = rangkings[row][col].size();
			ss << rangkings[row][col].substr(1,ranking_number_count-1);

			ss >> rank;
			one_body.push_back(rank);
		}
		number_rankings.push_back(one_body);
		one_body.clear();
	}

}


int main()
{
    int n = 200;

	vector > boysrankings;
	vector > girlsrankings;
	vector > boys_for_girls;
	vector > girls_for_boys;
	vector result;

	ObtainRinkings(boysrankings, "boys_rankings.txt", n);
	NumberRanking(boysrankings, boys_for_girls);
	ObtainRinkings(girlsrankings, "girls_rankings.txt", n);
	NumberRanking(girlsrankings, girls_for_boys);

	result = GaleShapley(boys_for_girls, girls_for_boys, n);

	cout << "配对结果为：";
	for (int i = 0; i < result.size(); i++)
	{
		if(i%5 == 0)
			cout << endl;
		cout.width(4); 
		cout << 'B' << i << "-" << 'G' << result[i] <<"	 ";
	}

	system("pause");
	return 0;
}

三. 算法分析

这个算法有排序的，且女的一旦匹配上，就不会被甩了，男的可能被甩掉，且每个人都是全排序的（指一个男的对所有女的一个排序），会有好的稳定结果。 如果出现不稳定的，即 M 一定是喜欢 w' 胜过w。 

时间复杂度 是O（n^2), 每个男的女的都进行 的话 才最大 了O（n^2）。

四. 算法扩展：

这个算法在高校录取志愿分配上， 医生的工作单位需求匹配上， 以及肾脏匹配 上有很大的应用。

五. 参考文献：

CS711008Z Algorithm Design and Analysis. Lecture 1. Introduction and some representative problems