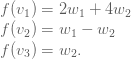线性代数: 什么是矩阵，以及矩阵的线性代数意义

  多数高中生学习矩阵和矩阵乘法，但是他们往往不知道为什么矩阵乘法是这样工作的。

  添加矩阵很简单: 只需添加相应的条目。 然而，矩阵乘法并不是这样工作的，对于一个不理解矩阵背后理论的人来说，这种矩阵相乘的方法可能看起来非常不自然和奇怪。

  为了真正理解矩阵，我们把它们看作是更大图景的一部分。 矩阵表示空间之间的函数，称为向量空间，也不是任何函数，而是线性函数。 这实际上就是线性代数关注矩阵的原因。

  关于矩阵的两个基本事实是: 每个矩阵表示一个线性函数，每个线性函数表示一个矩阵。

  因此，实际上在矩阵和线性函数之间存在双射。 我们将说明，乘法矩阵对应于对它们所表示的函数进行合成。接下来，我们将研究矩阵有什么好处，以及为什么线性代数首先兴起。

  最有可能的是，如果你在高中学过代数，你会看到下面这些东西:

你的高中代数老师可能告诉你这是一个“矩阵” 然后你学习了如何用矩阵做事情。 例如，你可以相加两个矩阵，操作相当直观:

你也可以减去矩阵，它的工作原理类似。 你可以用一个数字乘以一个矩阵:

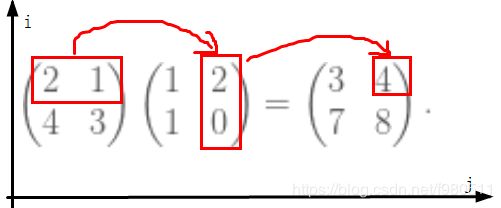
然后，当你学习如何乘法矩阵时，一切似乎都错了:

  也就是说，要找到乘积的第  i 行, j 列中的条目，你看第一个矩阵的第i行，第二个矩阵的第 j列，你把它们的相应数字相乘，然后你把结果加起来，得到那个位置的条目。

  在上面的例子中，第一行和第二列的条目结果是 4，因为第一个矩阵的第一行是，第二个矩阵的第二列是。 此外，这意味着矩阵乘法甚至不是交换的！ 如果我们按照上面的乘法顺序计算，那我们可以计算如下另外一个矩阵相乘进行学习，例如

 

为什么矩阵乘法不像加法和减法那样工作？ 如果乘法是这样运算的，那么除法到底是怎么运算的呢？ 这篇文章的目的就是回答这些问题。

为理解矩阵乘法为什么是这样工作的，有必要理解矩阵实际上是什么。 但是在我们开始之前，让我们简单的看一下为什么我们首先关心矩阵。

矩阵最基本的应用是求解线性方程组。

一个线性方程是所有变量单独出现而没有幂的方程; 它们不会相乘或相乘，也没有有趣的函数。 线性方程组的一个例子是

  这个系统的解是。 这样的方程式看似简单，但在生活中却很容易出现。

  例如，假设有两个朋友 舒克 和 贝塔 去买糖果。 舒克 买了2块巧克力和1袋彩虹糖，花了3块钱; 而 贝塔 买了4块巧克力和3袋彩虹糖，花了7块钱。 如果我们想知道巧克力棒和彩虹糖的价格，我们可以设定一块巧克力棒的价格 x，设定一包彩虹糖的价格 y，变量满足上述线性方程组。 因此我们可以很简单的推断出，一块巧克力和一包彩虹糖都要1块钱。 这个系统特别容易解决，因为人们可以猜测和检查的解决方案，但一般来说，用变量和方程式代来解决类似问题，会更困难些。 这就是矩阵的用武之地！ 请注意，到了矩阵乘法，上面的线性方程组可以改写为

如果我们能找到一个矩阵 A，它是矩阵的逆矩阵，那么如果我们将 A 同时乘在方程的两边，将左边的 约掉，右边增一个 A，我们就能得到

  矩阵的应用远远超出了这个简单的问题，但是现在我们将把它作为我们的动机。 让我们回到理解矩阵是什么。 为了理解矩阵，我们必须知道向量是什么。 向量空间是一个具有特定的集合，而向量是向量空间的元素。 现在，为了技术上的简单性，我们将只使用实数上的向量空间，也称为实向量空间（real vector space）。 一个真正的向量空间，基本上就是你想构成的空间。 例如线是一维实向量空间，x-y 平面是二维实向量空间，三维空间是三维实向量空间，等等。

  如果你在学校学过矢量，那么你可能很熟悉把它们想象成箭头，你可以把它们加在一起，乘以一个实数，等等，但是把矢量加在一起的结果是不同的。 这听起来熟悉吗？ 应该是的。 这就是矩阵的工作原理，这不是巧合。

关于空间向量最重要的事实是它们总是有基的。 向量空间的基础是一组向量，这样空间中的任何向量都可以写成这些向量的线性组合。 如果是你的基础向量（即每个维度上的一段单位向量），那么是一个线性组合，如果是实数，将也可以表示在这个向量空间中的任何一个向量。 一个具体的例子如下: x-y 平面的是基础向量。 那么任何向量的形式都可以写成

所以我们确实有一个基础！ 这不是唯一可能的基础。 事实上，在我们的基础上的向量，甚至不必是垂直的！ 例如，矢量构成了基础，因为我们可以写

.

现在，线性映射只是两个向量空间之间的一个函数，碰巧是线性的。 线性是一个非常好的性质。

如果下列两个属性成立，那么函数就是线性的:

  例如，该函数在实线限定上不是线性的，因为而。现在，我们将迄今为止所讨论的所有想法联系在一起：矩阵，基础和线性变换。即矩阵是线性变换的表示，你可以通过查看矩阵基础的作用来弄清楚如何写下矩阵。要理解第一个陈述，我们需要了解为什么第二个陈述是正确的。这个想法是任何向量都是基向量的线性组合，因此您只需要知道线性变换如何影响每个基向量。这是因为，由于函数是线性的，如果我们有一个可以写成线性组合的任意向量，那么

请注意，值完全由值决定，因此我们需要完全定义线性变换所需的所有信息。矩阵在哪里？那么，一旦我们选择线性变换的域和目标的基础，矩阵的列将表示函数下的基矢量的图像。例如，假设我们有一个映射到的线性变换，意味着它采用三维向量并吐出二维向量。现在只是一些抽象的功能，我们无法在纸上写下来。让我们为我们的域（3空间）和目标（2空间或平面）选择基础。一个不错的选择是前者和对于后者。我们需要知道的是如何影响，目标的基础是具体地写下价值观。我们函数的矩阵将是一个2乘3的矩阵，其中3列被索引，2行被索引。我们需要记下的就是价值观。具体来说，让我们说吧

然后相应的矩阵将是

这样做的原因是矩阵乘法的设计使得如果将矩阵乘以向量乘以除-th条目中的1之外的全零，则结果只是矩阵的第-列。你可以自己检查一下。因此我们知道矩阵在应用于（相乘）基矢量时可以正常工作。而且矩阵满足相同的性质的线性变换，即和，其中的载体和为实数。因此适用于所有向量，因此它是正确的表示。请注意，如果我们为基向量选择了不同的向量，则矩阵看起来会有所不同。因此，矩阵不是自然的，因为它们取决于我们选择的基础。

现在，最后回答一开始提出的问题。为什么矩阵乘法按照它的方式工作？让我们来看看我们在开始时使用的两个矩阵：和。我们知道，它们分别对应于线性函数在飞机上，让我们称他们和分别。乘法矩阵对应于组成  它们的函数。因此，做与任何向量相同。为了确定矩阵应该是什么样子，我们可以看到它如何影响基矢量。我们有

所以第一列应该是，和

所以第二列应该是。实际上，这与我们在开始时通过矩阵乘法得到的答案一致！虽然这根本不是一个严格的证明，因为它只是一个例子，它捕捉了矩阵乘法就是这样的原因。

现在我们已经了解矩阵乘法如何以及为什么按照它的方式工作，矩阵划分如何工作？您可能熟悉功能反转。 函数的逆是一个函数，使得所有函数。由于矩阵的乘法对应于函数的组合，所以只有矩阵的乘法逆是相应函数的组合逆才有意义。这就是为什么不是所有矩阵都有乘法逆。有些函数没有组合反转！例如，线性函数映射到定义由不具有逆，因为许多矢量被映射到相同的值（什么会是？？？）。这对应于1×2矩阵没有乘法逆的事实。因此，如果存在，则除以矩阵只是乘以。有用于计算矩阵求逆的算法，但我们会将其保存为另一篇文章