字符串匹配的三个算法（KMP+字典树+AC自动机）

字符串匹配的意思是给一个字符串集合，和另一个字符串集合，看这两个集合交集是多少。

（1）若是都只有一个字符串，那么就看其中一个是否包含另外一个（一对一，KMP）

https://blog.csdn.net/fkyyly/article/details/48007965

（2）若是父串集合（比较长的，被当做模板）的有多个，子串（拿去匹配的）只有一个，就是问这个子串是否存在于父串之中（字典树则是一对多的时候匹配常用算法，或者把字典里面的元素hash作为key但是这种方法存储空间比较大所以可以用字典树）

（3）若是子串父串集合都有多个，那么就是问交集了（AC自动机就是多对多的匹配或者用HashMap）

如给定5个单词：say she shr he her，然后给定一个字符串yasherhs。问一共有多少单词在这个字符串中出现过

1. 一对一KMP

2. 一对多Trie树

Trie中文名又叫做字典树，前缀树等，因为其结构独有的特点，经常被用来统计，排序，和保存大量的字符串，经常见于搜索提示，输入法文字关联等，当输入一个值，可以自动搜索出可能的选择。当没有完全匹配的结果时，可以返回前缀最为相似的可能。

基本性质：

1.根节点不含有字符，其余各节点有且只有一个字符。

2.根节点到某一节点中经过的节点存储的值连接起来就是对应的字符串。

3.每一个节点所有的子节点的值都不应该相同。

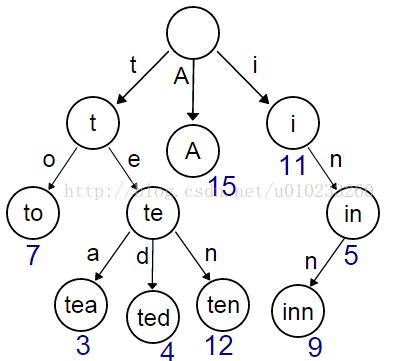
借用一下维基百科上的一张图片：

//定义前缀树数据结构
class TrieNode {
    TrieNode[] son;// TrieNode[26] in this case 存储直接的孩子节点
    boolean isEnd;// end of a string.
    char val;// No this field mostly.

    TrieNode() {
        son = new TrieNode[26];//26 letters.CaseInsensitive.只是给了26这个长度，但是里面具体有多少个元素表示有多少个son
        isEnd = false;
    }
}

public class One2Many {

    /**
     字典树的Java实现。实现了插入、查询
     */
    TrieNode root = new TrieNode();

    public void insert(String str) {
        if (str == null || str.length() == 0) {
            return ;
        }
        TrieNode node = root;
        char[] letters=str.toCharArray();
        for (int i = 0, len = str.length(); i < len; i++) {
            int pos = letters[i] - 'a';
            if (node.son[pos] == null) {
                node.son[pos] = new TrieNode();
                node.son[pos].val = letters[i];
            }
            node = node.son[pos];
        }
        node.isEnd = true;//每个单词的结束isEnd才为true，中间默认为flase
    }

    // search a word in the tree.Complete matching.
    public boolean has(String str) {
        if (str == null || str.length() == 0) {
            return false;
        }
        TrieNode node = root;
        char[] letters=str.toCharArray();
        for (int i = 0, len = str.length(); i < len; i++) {
            int pos = letters[i] - 'a';
            if (node.son[pos] != null) {
                node = node.son[pos];
            } else {
                return false;
            }
        }
        return node.isEnd;//只有走到末尾才返回true，如果是前缀也是false
    }

    //Trie树的根节点用特殊字符（这样下面就可以26个分支了）
    public static void main(String[] args) {
        One2Many tree = new One2Many();
        //用strs构建Trie树
        String[] strs={
                "banana",
                "band",
                "bee",
                "absolute",
                "acm",
        };
        for(String str:strs){
            tree.insert(str);
        }
        //判断一个元素在不在tire中也就是一个元素在不在另外一个集合中
        System.out.println(tree.has("band"));
    }
}

https://blog.csdn.net/u010233260/article/details/45752777

http://bylijinnan.iteye.com/blog/1525203

3. 多对多AC自动机或者Map

给一个字典，再给一个m长的文本（m长的文本里面包含很多的词），问这个文本里出现了字典里的哪些字。

3.1 方法一：使用HashMap复杂度是O(maxLengh(word)*length(str))这样和字典的大小没有关系

import java.util.ArrayList;
import java.util.HashMap;

/**
 * 一对多，把多的那个存入hashmap中
 * 应用场景最大正向匹配分词
 */

public class Many2Many {
    public void matchFun(String str){
        String[] dic = {"请", "播放", "一首", "黎明", "的", "太阳", "黎明的太阳"};
        HashMap dicMap = new HashMap<>();
        int maxLength = 0;
        for (int i = 0; i < dic.length; i++) {
            dicMap.put(dic[i], "1");
            maxLength = dic[i].length();
        }
        String temp = "";
        for (int length = maxLength; length > 0 ; length --) {
            for (int i = 0; i < str.length() && i+length < str.length()+1; i++) {
                temp = str.substring(i, i+length);
                if (dicMap.get(temp) != null){
                    System.out.println(temp);
                }
            }
        }
    }

    public static void main(String[] args) {
        One2Many many2Many = new Many2Many();
        Many2Many.matchFun("你好，请播放黎明的太阳");
    }
}

3.2 方法二：AC自动机

如果用AC自动机来解决的话，效率将为线性O(length(str))时间复杂度。

AC自动机也运用了一点KMP算法的思想。简述为字典树+KMP也未为不可。其实就是在trie树上做KMP。AC自动机增加了失败转移，转移到已经输入成功的文本的后缀，来实现。

首先讲一下acnode的结构：

与字典树相比，就多了个*fail对吧，这个就相当于KMP算法里的next数组。只不过它存的是失配后跳转的位置，而不是跳转之后再向前跳了多少罢了。

3.2.1.多模式匹配

　　多模式匹配就是有多个模式串P1,P2,P3...，Pm，求出所有这些模式串在连续文本T1....n中的所有可能出现的位置。

　　例如：求出模式集合{"nihao","hao","hs","hsr"}在给定文本"sdmfhsgnshejfgnihaofhsrnihao"中所有可能出现的位置。

3.2.2.Aho-Corasick算法　　

　　使用Aho-Corasick算法需要三步：

　　1.建立模式的Trie

　　2.给Trie添加失败路径

       其实就是后缀，如图中的sh的后缀是h（sh的fail指针指向h）

　　3.根据AC自动机，搜索待处理的文本

　　下面说明这三步：

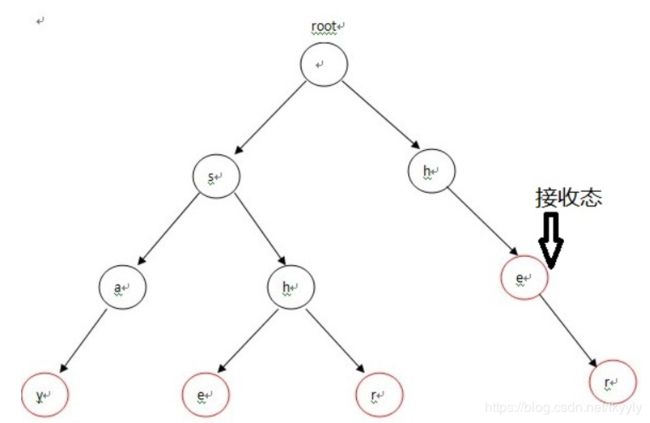
建立多模式集合的Trie树

　　Trie树也是一种自动机。对于多模式集合{"say","she","shr","he","her"}，对应的Trie树如下，其中红色标记的圈是表示为接收态：

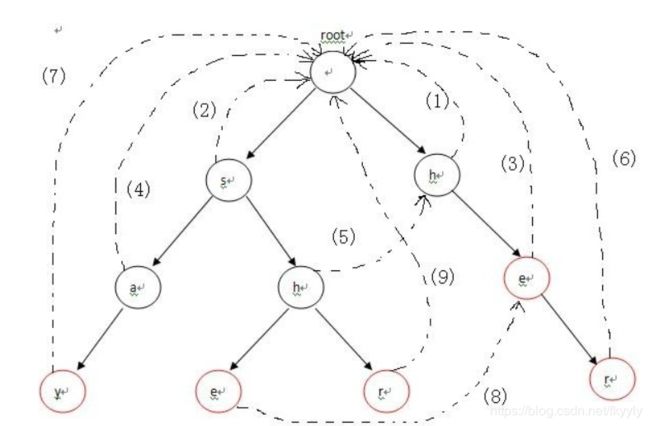
为多模式集合的Trie树添加失败路径，建立AC自动机

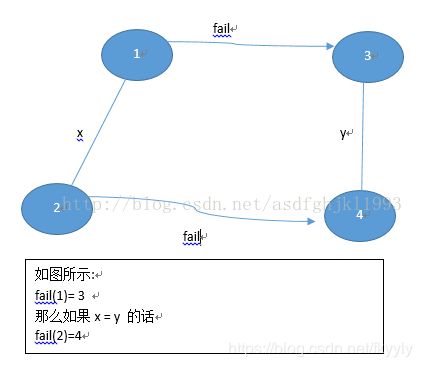
AC自动机里面比较难理解的应该是它的失配指针的计算过程。这个计算过程从本质上讲就是进行一遍广搜，于此同时维护fail指针，每一步的维护过程可用下图表示。

构造失败指针的过程概括起来就一句话：设这个节点上的字母为C，沿着他父亲的失败指针走，直到走到一个节点，他的儿子中也有字母为C的节点。然后把当前节点的失败指针指向那个字母也为C的儿子。如果一直走到了root都没找到，那就把失败指针指向root。

　　使用广度优先搜索BFS，层次遍历节点来处理，每一个节点的失败路径。　　

　　特殊处理：第二层要特殊处理，将这层中的节点的失败路径直接指向父节点(也就是根节点)。

 

时间复杂度

　　时间复杂度分为建立AC自动机的时间复杂度和匹配的时间复杂度。

　　设所有模式的长度和为n，文本长度为m。

建立前缀树的时间复杂度为O(n)，而建立fail指针的时间复杂度分析类似于KMP算法中建立跳转表的时间复杂度。我们可以定义每个结点x的fail指针指向的y结点的深度为x的“子深”，记作x.cd。很容易发现x.cd<=x.father.cd+1，而我们每次从x.father出发沿着fail指针移动，x的子深也在不断递减但不会低于0，在为某个模式上的结点建立fail时，每次后移最多提供1个子深，因此在创建模式pi时我们最多沿着fail指针移动了|pi|次，故创建所有模式总共沿着fail指针最多移动O(n)次，到此说明了建立fail指针的时间复杂度为O(n)。

　　对模式匹配，每当我们读入一个字符c时，trace或者向下移动（即有c号孩子）并结束或者沿着fail移动到某个自己的后缀上去。显然向下移动最多发生O(m)次，而沿着fail移动，就如同我所说的每次都必定会降低子深，而每次向下移动可以提供最多1子深，因此可以保证沿着fail移动的次数最多为O(m)次。故总的时间复杂度为O(m)。

　　时间复杂度的总和为O(n+m)，空间复杂度为O(Cn)，其中C为使用的字符集的大小（用于建立前缀树）

https://blog.csdn.net/asdfghjkl1993/article/details/43371951

http://www.cnblogs.com/xudong-bupt/p/3433506.html

https://blog.csdn.net/qq_30346729/article/details/7883504