收藏
707
-
迪杰斯特拉算法
编辑
迪杰斯特拉算法是由荷兰计算机科学家 狄克斯特拉于1959 年提出的,因此又叫 狄克斯特拉算法。是从一个顶点到其余各顶点的 最短路径算法,解决的是有向图中最短路径问题。迪杰斯特拉算法主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。
[1]
- 迪克斯特拉算法
- Dijkstra's Algorithm
- 计算机算法
- 单源最短路径问题
目录
Dijkstra算法是典型的 算法。 Dijkstra算法是很有代表性的 算法。Dijkstra一般的表述通常有两种方式,一种用永久和临时标号方式,一种是用 OPEN, CLOSE表的方式,这里均采用永久和临时标号的方式。注意该算法要求图中不存在负权边。
[2]
1.首先,引入一个辅助向量D,它的每个分量 D
 表示当前所找到的
从起始点
表示当前所找到的
从起始点
 (即源点
(即源点
 )到其它每个顶点
)到其它每个顶点
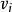 的长度。
的长度。
例如,D[3] = 2表示从起始点到顶点3的路径相对最小长度为2。这里强调相对就是说在算法执行过程中D的值是在不断逼近最终结果但在过程中不一定就等于长度。
[1]
2.D的初始状态为:若从
 到
到
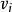 有弧(即从
有弧(即从
 到
到
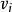 存在连接边),则D
存在连接边),则D
 为弧上的权值(即为从
为弧上的权值(即为从
 到
到
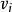 的边的权值);否则置D
的边的权值);否则置D
 为∞。
为∞。
显然,长度为 D
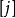 = Min{ D |
= Min{ D |
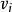 ∈V } 的路径就是从
∈V } 的路径就是从
 出发到顶点
出发到顶点
 的长度最短的一条路径,此路径为(
的长度最短的一条路径,此路径为(
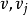 )。
)。
3.那么,下一条长度次短的是哪一条呢?也就是找到从源点
 到下一个顶点的最短路径长度所对应的顶点,且这条最短路径长度仅次于从源点
到下一个顶点的最短路径长度所对应的顶点,且这条最短路径长度仅次于从源点
 到顶点
到顶点
 的最短路径长度。
的最短路径长度。
假设该次短路径的终点是
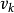 ,则可想而知,这条路径要么是(
,则可想而知,这条路径要么是(
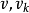 ),或者是(
),或者是(
 )。它的长度或者是从
)。它的长度或者是从
 到
到
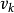 的弧上的权值,或者是D
的弧上的权值,或者是D
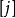 加上从
加上从
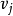 到
到
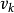 的弧上的权值。
的弧上的权值。
4.一般情况下,假设S为已求得的从源点
 出发的最短路径长度的顶点的集合,则可证明:下一条次最短路径(设其终点为
出发的最短路径长度的顶点的集合,则可证明:下一条次最短路径(设其终点为
 )要么是弧(
)要么是弧(
 ),或者是从源点
),或者是从源点
 出发的中间只经过S中的顶点而最后到达顶点
出发的中间只经过S中的顶点而最后到达顶点
 的路径。
的路径。
因此,下一条长度次短的的最短路径长度必是D
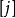 = Min{ D
= Min{ D
 |
|
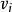 ∈V-S },其中D
∈V-S },其中D
 要么是弧(
要么是弧(
 )上的权值,或者是D
)上的权值,或者是D
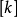 (
(
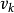 ∈S)和弧(
∈S)和弧(
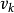 ,
,
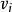 )上的权值之和。
)上的权值之和。
算法描述如下:
1)令arcs表示弧上的权值。若弧不存在,则置arcs为∞(在本程序中为MAXCOST)。S为已找到的从
 出发的的终点的集合,初始状态为空集。那么,从
出发的的终点的集合,初始状态为空集。那么,从
 出发到图上其余各顶点
出发到图上其余各顶点
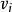 可能达到的长度的初值为D=arcs[Locate Vex(G,
可能达到的长度的初值为D=arcs[Locate Vex(G,
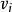 )],
)],
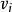 ∈V;
∈V;
2)选择
 ,使得D
,使得D
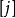 =Min{ D |
=Min{ D |
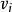 ∈V-S } ;
∈V-S } ;
3)修改从
 出发的到集合V-S中任一顶点
出发的到集合V-S中任一顶点
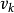 的最短路径长度。
[1]
的最短路径长度。
[1]
在 无向图 G=(V,E) 中,假设每条边 E[i] 的长度为 w[i],找到由顶点 V0 到其余各点的最短值。
[2]
按路径长度 递增次序产生算法:
把顶点集合V分成两组:
(1)S:已求出的顶点的集合(初始时只含有源点V0)
(2)V-S=T:尚未确定的顶点集合
将T中顶点按递增的次序加入到S中,保证:
(1)从源点V0到S中其他各顶点的长度都不大于从V0到T中任何顶点的最短路径长度
(2)每个顶点对应一个距离值
S中顶点:从V0到此顶点的长度
T中顶点:从V0到此顶点的只包括S中顶点作中间顶点的最短路径长度
依据:可以证明V0到T中顶点Vk的,或是从V0到Vk的直接路径的权值;或是从V0经S中顶点到Vk的路径权值之和
( 反证法可证)
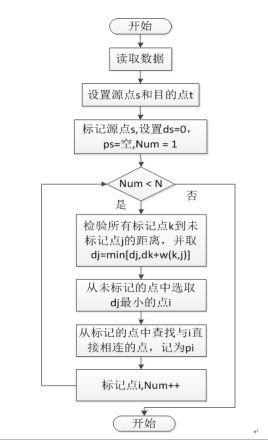
求最短路径步骤
算法步骤如下:
G={V,E}
1. 初始时令 S={V0},T=V-S={其余顶点},T中顶点对应的距离值
若存在,d(V0,Vi)为弧上的权值
若不存在,d(V0,Vi)为∞
2. 从T中选取一个与S中顶点有关联边且权值最小的顶点W,加入到S中
3. 对其余T中顶点的距离值进行修改:若加进W作中间顶点,从V0到Vi的距离值缩短,则修改此距离值
重复上述步骤2、3,直到S中包含所有顶点,即W=Vi为止
pascal语言
下面是该算法的Pascal程序
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
|
type
bool=
array
[
1..10
]ofboolean;
arr=
array
[
0..10
]ofinteger;
var
a:
array
[
1..10
,
1..10
]ofinteger;
//存储图的邻接数组,无边为10000
c,d,e:arr;
//c为最短路径数值,d为各点前趋,
t:bool;
//e:路径,t为辅助数组
i,j,n,m:
integer
;
inf,outf:text;
procedureinit;
//不同题目邻接数组建立方式不一样
begin
assign(inf,inputfile);
assign(outf,outputfile);
reset(inf);
rewrite(outf);
read(inf,n);
fori:=1tondo
begin
forj:=1tondo
begin
read(inf,a[i,j]);
ifa[i,j]=0then
a[i,j]:=
10000
;
end
;
end
;
end
;
proceduredijkstra(qi:
integer
;t:bool;varc
{,d}
:arr);
//qi起点,{}中为求路径部分,不需求路径时可以不要
var
i,j,k,min:
integer
;
begin
t[qi]:=
true
;
//t数组一般在调用前初始,除起点外所有节点都化成false,也可将部分点初始化成true以回避这些点
fori:=1tondo
d[i]:=qi;
d[qi]:=
0
;
fori:=1tondo
c[i]:=a[qi,i];
fori:=1ton-1do
begin
min:=maxint;
//改为最大值
forj:=1tondo
if
(c[j]begin
k:=j;
min:=c[j];
end
;
t[k]:=
true
;
forj:=1tondo
if
(c[k]+a[k,j]begin
c[j]:=c[k]+a[k,j];
d[j]:=k;
end
;
end
;
end
;
proceduremake(zh:
integer
;d:arr;vare:arr);
//生成路径,e[0]保存路径
var
i,j,k:
integer
;
//上的节点个数
begin
i:=
0
;
whiled[zh]<>0do
begin
inc(i);
e[i]:=zh;
zh:=d[zh];
end
;
inc(i);
e[i]:=qi;
e[
0
]:=i;
end
;
|
主程序调用:求长度:初始化t,然后dijkstra(qi,t,c,d)
求路径:make(m,d,e) ,m是终点
java语言
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
//初始化路径,都为最大值。
intpath[][]=newint[n+
1
][n+
1
];
for
(inti=
1
;ifor
(intj=
1
;jpath[i][j]=Integer.MAX_VALUE;
}
//这里需要输入path[i][j]的具体内容,如果有重复数据的话,需要更新路径为最小值。
intminLen[]=newint[n+
1
];
//visit初始为0,防止回溯
intvisit[]=newint[n+
1
];
//初始化1到其他点的距离。
for
(inti=
1
;iminLen[i]=path[
1
][i];
}
voidDijkstra(){
minLen[
1
]=
0
;
visit[
1
]=
1
;
intminj=
1
;
for
(inti=
1
;iintmin=Integer.MAX_VALUE;
for
(intj=
1
;jif
(visit[j]==
0
&&minLen[j]min=minLen[j];
minj=j;
}
}
visit[minj]=
1
;
for
(intj=
1
;jif
(visit[j]==
0
&&minLen[minj]!=Integer.MAX_VALUE&&path[minj][j]!=
Integer.MAX_VALUE&&minLen[j]>(minLen[minj]+path[minj][j])){
minLen[j]=minLen[minj]+path[minj][j];
}
}
}
}
|
C语言
下面是该算法的C语言实现
[1]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
#include
#include
#define max 11000000000
inta[1000][1000];
intd[1000];
//d表示某特定边距离
intp[1000];
//p表示永久边距离
inti,j,k;
intm;
//m代表边数
intn;
//n代表点数
intmain()
{
scanf
(
"%d%d"
,&n,&m);
intmin1;
intx,y,z;
for
(i=1;i<=m;i++)
{
scanf
(
"%d%d%d"
,&x,&y,&z);
a[x][y]=z;
a[y][x]=z;
}
for
(i=1;i<=n;i++)
d[i]=max1;
d[1]=0;
for
(i=1;i<=n;i++)
{
min1=max1;
for
(j=1;j<=n;j++)
if
(!p[j]&&d[j]{
min1=d[j];
k=j;
}
p[k]=j;
for
(j=1;j<=n;j++)
if
(a[k][j]!=0&&!p[j]&&d[j]>d[k]+a[k][j])
d[j]=d[k]+a[k][j];
}
for
(i=1;iprintf
(
"%d->"
,p[i]);
printf
(
"%d\n"
,p[n]);
return0;
}
|
大学经典教材<<数据结构>>(C语言版 严蔚敏 吴为民 编著) 中该算法的实现
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
|
/*
测试数据 教科书 P189 G6 的邻接矩阵 其中 数字 1000000 代表无穷大
6
1000000 1000000 10 100000 30 100
1000000 1000000 5 1000000 1000000 1000000
1000000 1000000 1000000 50 1000000 1000000
1000000 1000000 1000000 1000000 1000000 10
1000000 1000000 1000000 20 1000000 60
1000000 1000000 1000000 1000000 1000000 1000000
结果:
D[0] D[1] D[2] D[3] D[4] D[5]
0 1000000 10 50 30 60
*/
#include
#include
#define MAX 1000000
using
namespace
std;
int
arcs[10][10];
//邻接矩阵
int
D[10];
//保存最短路径长度
int
p[10][10];
//路径
int
final[10];
//若final[i] = 1则说明 顶点vi已在集合S中
int
n = 0;
//顶点个数
int
v0 = 0;
//源点
int
v,w;
void
ShortestPath_DIJ()
{
for
(v = 0; v < n; v++)
//循环 初始化
{
final[v] = 0; D[v] = arcs[v0][v];
for
(w = 0; w < n; w++) p[v][w] = 0;
//设空路径
if
(D[v] < MAX) {p[v][v0] = 1; p[v][v] = 1;}
}
D[v0] = 0; final[v0]=0;
//初始化 v0顶点属于集合S
//开始主循环 每次求得v0到某个顶点v的最短路径 并加v到集合S中
for
(
int
i = 1; i < n; i++)
{
int
min = MAX;
for
(w = 0; w < n; w++)
{
//我认为的核心过程--选点
if
(!final[w])
//如果w顶点在V-S中
{
//这个过程最终选出的点 应该是选出当前V-S中与S有关联边
//且权值最小的顶点 书上描述为 当前离V0最近的点
if
(D[w] < min) {v = w; min = D[w];}
}
}
final[v] = 1;
//选出该点后加入到合集S中
for
(w = 0; w < n; w++)
//更新当前最短路径和距离
{
/*在此循环中 v为当前刚选入集合S中的点
则以点V为中间点 考察 d0v+dvw 是否小于 D[w] 如果小于 则更新
比如加进点 3 则若要考察 D[5] 是否要更新 就 判断 d(v0-v3) + d(v3-v5) 的和是否小于D[5]
*/
if
(!final[w] && (min+arcs[v][w]
{
D[w] = min + arcs[v][w];
// p[w] = p[v];
p[w][w] = 1;
//p[w] = p[v] + [w]
}
}
}
}
int
main()
{
cin >> n;
for
(
int
i = 0; i < n; i++)
{
for
(
int
j = 0; j < n; j++)
{
cin >> arcs[i][j];
}
}
ShortestPath_DIJ();
for
(
int
i = 0; i < n; i++)
printf
(
"D[%d] = %d\n"
,i,D[i]);
return
0;
}
|
思考
该 算法复杂度为n^2,我们可以发现,如果边数远小于n^2,对此可以考虑用 堆这种 数据结构进行优化,取出最短路径的复杂度降为O(1);每次调整的复杂度降为O(elogn);e为该点的边数,所以复杂度降为
O((
m+
n)log
n)。
实现
1. 将与源点相连的点加入 堆,并调整堆。
2. 选出堆顶元素u(即代价最小的元素),从堆中删除,并对堆进行调整。
3. 处理与u相邻的,未被访问过的,满足三角不等式的顶点
1):若该点在堆里,更新距离,并调整该元素在堆中的位置。
2):若该点不在堆里,加入堆,更新堆。
4. 若取到的u为终点,结束算法;否则重复步骤2、3。
代码
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
|
procedureDijkstra;
var
u,v,e,i:
longint
;
begin
fillchar(dis,sizeof(dis),
$7e
);
//距离
fillchar(Inh,sizeof(Inh),
false
);
//是否在堆中
fillchar(visit,sizeof(visit),
false
);
//是否访问过
size:=
0
;
e:=last[s];
whilee<>0do
//步骤1
begin
u:=other[e];
ifnot(Inh[u])
then
//不在堆里
begin
inc(size);
heap[size]:=u;
dis[u]:=cost[e];
Loc[u]:=size;
//Loc数组记录元素在堆中的位置
Inh[u]:=
true
;
Shift_up(Loc[u]);
//上浮
end
else
ifcost[e]begin
dis[u]:=cost[e];
Shift_up(Loc[u]);
Shift_down(Loc[u]);
end
;
e:=pre[e];
end
;
visit[s]:=
true
;
whiletruedo
begin
u:=heap[
1
];
//步骤2
ifu=tthenbreak;
//步骤4
visit[u]:=
true
;
heap[
1
]:=heap[size];
dec(size);
Shift_down(
1
);
e:=last[u];
whilee<>0do
//步骤3
begin
v:=other[e];
ifNot(visit[v])
and
(dis[u]+cost[e]ifInh[v]
then
//在堆中
begin
dis[v]:=dis[u]+cost[e];
Shift_up(Loc[v]);
Shift_Down(Loc[v]);
end
else
//不再堆中
begin
inc(size);
heap[size]:=v;
dis[v]:=dis[u]+cost[e];
Loc[v]:=size;
Inh[v]:=
true
;
Shift_up(Loc[v]);
end
;
e:=pre[e];
end
;
end
;
writeln
(dis[t]);
end
;
|
- 参考资料
词条标签: