gmoj 1914. 【2011集训队出题】最短路

题目描述

Description

给一个N个点M条边的连通无向图，满足每条边最多属于一个环，有Q组询问，每次询问两点之间的最短路径。

Input

输入的第一行包含三个整数，分别表示N和M和Q
下接M行，每行三个整数v，u，w表示一条无向边v-u，长度为w
最后Q行，每行两个整数v，u表示一组询问

Output

输出Q行，每行一个整数表示询问的答案

Sample Input

9 10 2
1 2 1
1 4 1
3 4 1
2 3 1
3 7 1
7 8 2
7 9 2
1 5 3
1 6 4
5 6 1
1 9
5 7

Sample Output

5
6

Data Constraint

对于5%的数据，N<=100
对于20%的数据，N<=1000
对于100%的数据，N<=10000，Q<=10000

---

题解

Solution 1

圆方树裸题（然而我不会）

Solution 2

这应该是这题最水的解法了吧（好像是题解做法）！
发现这个仙人掌十分难搞，如果它是一棵树就容易处理了！
因此我们考虑怎么把仙人掌变成一棵树。
由于一条边最多只属于一个环，因此只用在每个环删除一条边，就可以变成一棵树了。
我们不妨以1号点为源点，跑一遍spfa，只保留那些更新到最短路的边，这就变成了一棵树。
这棵树有一个十分优良的性质：u,v两个点向上跳时，途经的所有环中，走树边是最优的（lca的那个环除外）
那么lca那个环怎么办呢？发现一个环只有2种走法，因此我们记录一下每一个环的边权和，用终点环的大小减去走树边的和，得出走非树边的路径长度。
可能上面的讲法有点晕，那么上一个图吧！

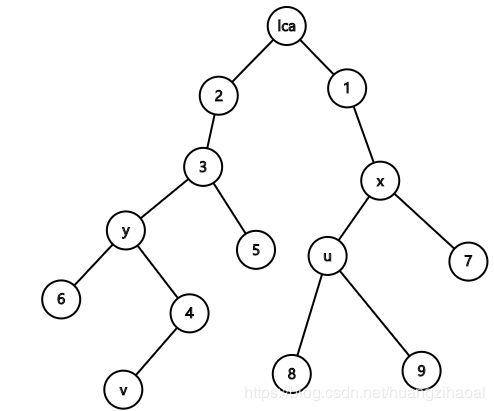
假设u和v是起点，lca,x,y在同一个环上，x和y是从u和v出发最先进入这个环的点，即u和v的祖先中最先在环上的2个点。
答案就是$di{s}_{u->x}+di{s}_{v->y}+\min (di{s}_{x->lca}+di{s}_{y->lca},SumOfCircle-di{s}_{x->lca}-di{s}_{y->lca})$
怎么求dis呢？这个很简单，我们不是已经求了最短路了吗？其实可以发现这个东西是相当于树上差分的，因此距离可以直接算出来。
那x和y呢？我们可以再维护一个倍增数组 ，表示编号为 i 的点往上跳 步，经过的最后一条边的编号。于是我们求lca时就可以得出u和v分别经过的最后一条边所在的环设为xx和yy，然后再分别从u和v出发往上倍增向lca靠拢，要求经过的最后一条边所在的环不能是xx（从v向上跳的话就是yy），就可以得出x和y了。

---

CODE

#include
using namespace std;
#define M 40005
#define N 10005
int dis[N],fir[N],nex[M],len[M],to[M],f[N][15],e[N][15],id[M],tot[M],data[M],dep[N],s=1,n,xx,yy;
bool exist[N];
inline void swap(int &x,int &y){int t=x;x=y,y=t;}
inline void spfa()
{
	int head=0,tail=1,u,v,i;
	for(i=2;i<=n;++i) dis[i]=0x3f3f3f3f;
	data[1]=dep[1]=1;
	while(head<tail)
	{
		u=data[++head],exist[u]=0;
		for(i=fir[u];i;i=nex[i])
		{
			v=to[i];
			if(dis[v]>dis[u]+len[i>>1])
			{
				dep[v]=dep[u]+1;
				dis[v]=dis[u]+len[i>>1];
				f[v][0]=u,e[v][0]=i>>1;
				if(!exist[v])
				{
					exist[v]=1;
					data[++tail]=v;
				}
			}
		}
	}
}
inline int getlca(int x,int y)//倍增lca
{
	bool judge=0;xx=yy=0;
	if(dep[x]<dep[y]) swap(x,y),judge=1;
	for(int i=14;i>=0;--i)
		if(dep[f[x][i]]>=dep[y])
			xx=e[x][i],x=f[x][i];
	if(x==y)
	{
		if(judge) yy=xx,xx=0;
		return x;
	}
	for(int i=14;i>=0;--i)
		if(f[x][i]!=f[y][i])
			x=f[x][i],y=f[y][i];
	xx=e[x][0],yy=e[y][0];
	if(judge) swap(xx,yy);
	return f[x][0];
}
inline int jump(int x,int lca,int num)//求第一个进入环的点
{
	for(int i=14;i>=0;--i)
		if(dep[f[x][i]]>=dep[lca]&&id[e[x][i]]!=num)
			x=f[x][i];return x;
}
int main()
{
	int m,q,i,j,x,y,z,ans,a,fx,fy;
	scanf("%d%d%d",&n,&m,&q);
	for(i=1;i<=m;++i)
		scanf("%d%d%d",&x,&y,len+i),
		to[++s]=y,nex[s]=fir[x],fir[x]=s,
		to[++s]=x,nex[s]=fir[y],fir[y]=s;
	spfa();
	for(j=1;j<15;++j)
		for(i=1;i<=n;++i)
			f[i][j]=f[f[i][j-1]][j-1],
			e[i][j]=e[f[i][j-1]][j-1];
	for(i=1,s=0;i<=m;++i)
	{
		x=to[i<<1],y=to[i<<1|1];
		if(dep[x]<dep[y]) swap(x,y);
		if(f[x][0]!=y)
		{
			tot[++s]=dis[x]+dis[y]+len[i];
			while(dep[x]>dep[y])
				id[e[x][0]]=s,x=f[x][0];
			while(x!=y)
			{
				id[e[x][0]]=id[e[y][0]]=s,
				x=f[x][0],y=f[y][0];
			}
			tot[s]-=dis[x]<<1;
		}
	}
	while(q--)
	{
		scanf("%d%d",&x,&y);
		z=getlca(x,y);
		if(id[xx]&&id[xx]==id[yy])
		{
			fx=jump(x,z,id[xx]);
			fy=jump(y,z,id[yy]);
			ans=dis[x]-dis[fx]+dis[y]-dis[fy];
			a=dis[fx]-dis[z]+dis[fy]-dis[z];
			if(tot[id[xx]]-a>a) ans+=a;
			else ans+=tot[id[xx]]-a;
		}
		else
		{
			if(id[xx])
			{
				fx=jump(x,z,id[xx]);
				ans=dis[x]-dis[fx];
				a=dis[fx]-dis[z];
				if(tot[id[xx]]-a>a) ans+=a;
				else ans+=tot[id[xx]]-a;
			}
			else ans=dis[x]-dis[z];
			if(id[yy])
			{
				fy=jump(y,z,id[yy]);
				ans+=dis[y]-dis[fy];
				a=dis[fy]-dis[z];
				if(tot[id[yy]]-a>a) ans+=a;
				else ans+=tot[id[yy]]-a;
			}
			else ans+=dis[y]-dis[z];
		}
		printf("%d\n",ans);
	}
	return 0;
}