深度卷积神经网络的数字实现——二维卷积的纯数字电路实现（二）

继第一篇卷积神经网络博客，这里继续更新后文。

3 数字模块实现方案

3.1 总体模块

总体模块不做过多说明，详细请看各底层子模块的介绍。

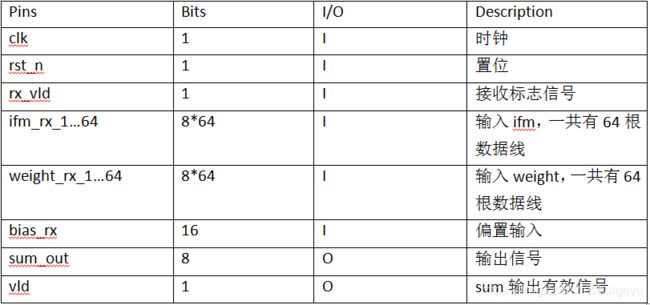
3.1.1 接口定义

3.2 乘法器子模块

3.2.1 模块功能

实现两个8位有符号数之间的乘法，并输出一个16位的数据。对输出结果不进行截取或饱和处理，保证数据的完备性。

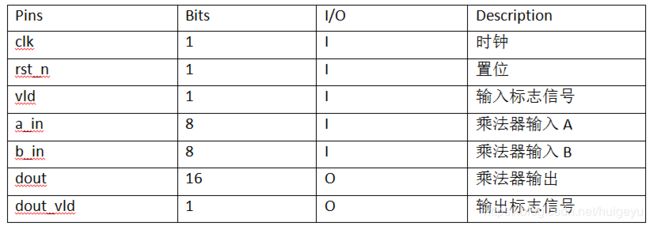
3.2.2 接口定义

3.2.3 实现方案

本乘法器采用类似booth乘法器的算法，并在其基础上作加速处理。

1.输入被乘数A和乘数B，并存储在相应的寄存器中，同时声明16位的P空间；
2.将乘数A直接存入P空间；
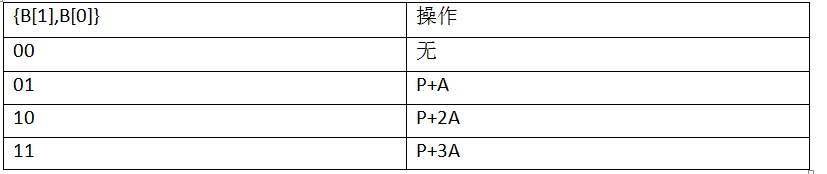
3.读取乘数B的最低两位，对被乘数A执行相关的操作，并将其存入P空间，相关操作如下表；
4.将乘数B右移两位，并重复步骤2，总共重复n/2次（n位乘数B的位宽）；
5.执行完n/2次后，P空间中的数据即为输出结果。

（表中P指的是P空间中数据的值。）

3.3 weight_manage子模块

3.3.1 模块功能

把从TOP.v接收到的weight存储器进行格式重排列，排列成从低到高，每9个为一个输出通道对应的3x3卷积核，并将新格式的weight存储器输出。

3.3.2 接口定义

3.4 加法器子模块

3.4.1 模块功能

本设计加法器包括3种：2输入加法器、64输入加法器、9输入加法器。分别对应到输出通道计算中的偏置相加，输入64通道的卷积输出结果的相加和每个卷积运算部分的9数相加（3×3模板中对应元素相乘之后得到9数相加），其中2输入加法器和9输入加法器是底层加法器模块，9输入加法器用于64输入加法器的构建以及卷积计算中。
之所以没有将加法器的输入端口数量进行模块化设计，
原因有二：
其一是端口数量的模块化在代码建模时不好设计；
其二是本设计中实涉及到的最底层加法器模块只有2输入和9输入两种。64输入模块的实现实际上是通过将9输入加法器例化8次（每个module中将其中一个输入置0）而得到。实际上，2输入与9输入加法器的最基本实现思路是完全一致的，故而以下以2输入加法器为例进行说明。

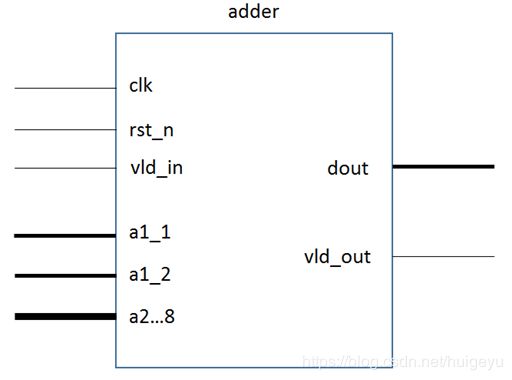
3.4.2 接口定义

上图是2输入加法器symbol，以其为例对加法器模块进行如下说明。加法器模块的输入输出接口定义由下表3-4-1列出。

3.4.3 实现方案

本加法器与一般的加法器不同的是，它采用将输入数据位宽进行最大值拓宽之后，然后再进行相加（无需考虑数的正负）。而一般的加法器实现，需要先进行正负判断，如果为负数需要先按补码方式操作，即除去最高位之后，剩余位数按位取反再加1，此后，便于两正数的加法是一样的，仅需做加即可。

本次设计的加法器，本质上讲，是因为对输入数据进行了位宽拓展。

举例：若a1=4（8’b0000_0100），a2=-3（8’b1111_1101），括号内为拓展方式，结果sum=8’b0000_0001，换算为有符号数就是1，知结果正确。唯一值得注意的是，如果是2输入8bit数据，其输出数据位宽许定义为8+1，如果是8输入，则需定义为8+3，即对数关系拓展位宽。

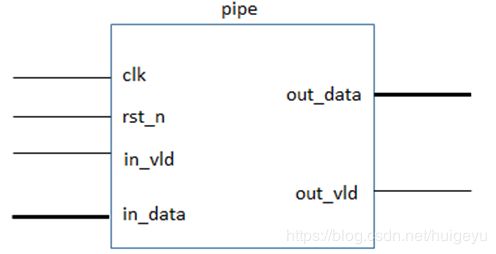
3.5 打拍子模块

3.5.1 模块功能

该模块主要实现对输入数据的打拍操作，打拍的次数由用户通过paramter决定。实际在时序对接时，经常遇到时序错位的问题，如某个脉冲信号或数据与理想的始终没有对齐，从而影响实际功能。通过调用打拍器模块，能够随意进行打拍操作，对时序的对齐起到立竿见影的效果。

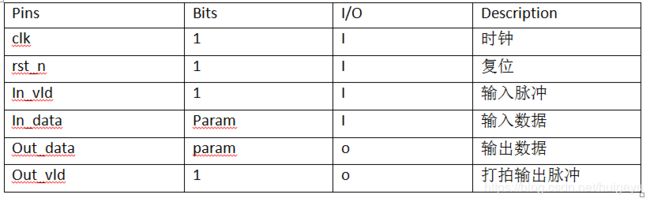
3.5.2 接口定义

如下图3-5-1所示，为打拍器的symbol示意图。

打拍器的输入输出接口的具体说明详见下表3-5-1。

3.5.3 实现方案

打拍器的实现主要是利用触发器的寄存功能，利用generate for语句，通过把上一个时钟的数据进行寄存，使用parameter生命需要打拍的次数，进而实现任意时钟个数的打拍。具体的功能代码详见相关文档。

3.6 卷积操作子模块

3.6.1 模块功能

卷积模块是一个小的功能模块，也是本次算法设计中核心的一环。卷积的实现需要对输入的ifm数据和wgt数据对应相乘，并将乘积结果进行相加。此外，卷积最开始需要对输入的卷积核3*3模板进行翻折运算（此翻转不是指左右翻转，而是指将模板选择180°所得）。

再对卷积的运算量进行评估，输入通道为64通道的32×32的8bit数据（64×1024个数据），卷积核数量为128通道的3×3的8bit数据（1152个数据），实际上，对每个卷积核的元素，分别要与输入ifm的每个元素进行相乘，则总共的乘法次数为1024×9，那么每输入通道就是1024×9×128，64输入通道，则共有乘法数量（不是乘法器的个数）为：1024×128×64×9次。

而题目要求中，限定乘法器数量不得超过2048个，很明显更多的乘法器数量可以换来更快的运算速度。在实际处理中，共用了9×64个乘法器，这远远小于题目设定值，节约了硬件资源的同时，牺牲了电路的速度。然而，这也并不是不能改变的，实际上可以通过增加乘法器数量的方式来提速（对输入数据进行并行处理，即一部分数据通过原有的乘法器进行运算，同时另一部分数据通过其他的乘法器运算）。本次设计中乘法器的具体分配是：对输入通道进行一一分配，而每个输入通道需要9个乘法器，即3×3模板卷积所需的9个乘法器，则共消耗9×64个乘法器资源。

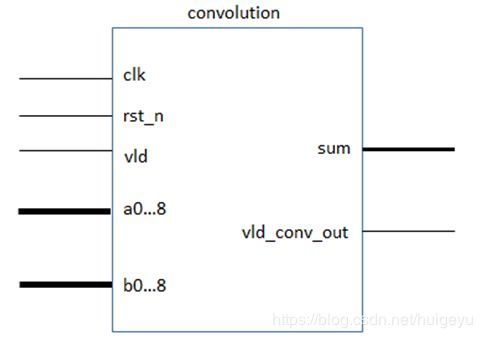
3.6.2 接口定义

下图3-6-1所示，为卷积模块的symbol示意图。

卷积模块于功能实现而言至关重要，但其输入输出端口相对简明，具体如下表3-6-1所示.

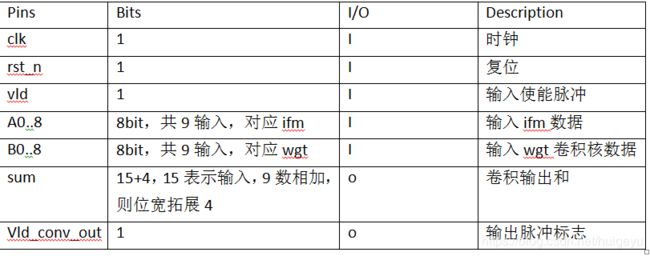
3.6.3 实现方案

化繁为简，实际上卷积就是简单的数学运算，即乘法和加法。对于底层子模块的数量，则有模板大小决定，本设计中针对3×3的输入模板，则共需要9个乘法器和1个9输入加法器模块。加法器模块原理与之前的2输入加法器模块相同，此处不赘述。

唯一声明的一点是：该模块没有考虑输入卷积核模板的翻折操作（旋转180°），这是因为，该操作实际上就是讲输入数据的0-8编程8-0，那么，具体实现时，顶层模块例化时直接通过端口的对接顺序的不同，实际上就巧妙的实现了卷积的翻折操作。

3.7 单通道全卷积模块

3.7.1 模块功能

顾名思义，该模块实现的功能是对每个输入通道的1024个输入ifm数据进行卷积操作，并通过串行总线输出求和数据。因为每个输入通道要对应128个输出卷积核，故而该模块输出的数据个数为1024×128，即128通道的32*32的数据，该数据尚未经过任何数据处理（如池化操作、激活以及数据位宽处理等），所以该数据数据的位宽是比较大（主要是因为实现过程中位宽在不断累积，加法和乘法导致）。

该模块实现后，需要将其例化64次（对应输入64通道），最后将该64例化module的输出再次进行相加，以及加上偏置数据，就能够得到携带信息较多的输出数据。

3.7.2 接口定义

下图3-7-1所示，为单通道全卷积模块symbol示意图。

以下通过表3-7-1，对该模块的输入输出端口进行介绍。

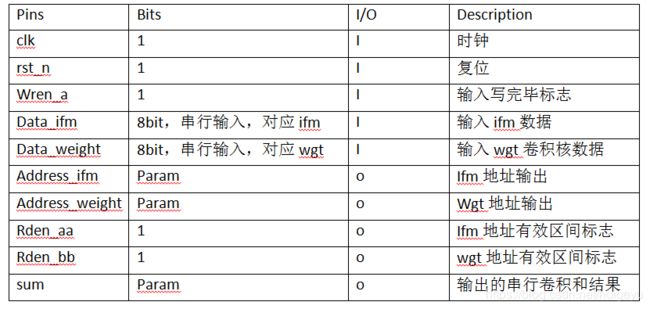
3.7.3 实现方案

该模块需要对每个输入通道ifm和wgt进行操作。事先经过处理存在ram中的数据，便是该模块所需的，在写ram结束之后，该模块使能工作，通过对外输出读使能和读地址信号，进而实现从ram中是定地址拿数据。但在具体实现上，实际上采用了一个地址译码的算法。

首先，明确，每次应该取9个数，然后才能进行卷积操作，其次，wgt数据的读取和ifm数据的读取快慢不同（因为每9个wgt数据，会对一个1024个输入ifm数据，即每取1024个ifm数据，wgt才变化1轮）。这里，最大问题是，输入的数据是存放在1位数组里面，实际上需要映射到二维矩阵中，并且通过卷积核模板以步进1pad移动进行框选数据时，ifm的数据不是连续递增的，如输出的第一个卷积和对应的输入ifm的9个数地址是：-32，-31，-30；0，1，2；32，33，34。

故需要设计地址重译码算法，每次输出正确的9个ram读取地址，对于为负数的情况，实际上可以特殊处理，实际上为负数的地址就一定对应pad之后的最外层的数据，一般是0，在设计时以0冠之。这样，本设计将32*32的输入二维矩阵，分成9种不同的方位元素，即左上、右上、左下、右下、上边、左边、右边、下边以及内部，每种不同的case中，输出的9个地址都可以进行归一分类，这也是如此分类的原因之一。如，对于左上角即0地址，对应3×3模板的1,2,3,4,5,6,7,8,9，实际上只有5、6、8、9地址才会向ifm_ram中取数，其他情况均为0。其他8中case的情形类似可得。

3.8 全卷积池化激活模块

3.8.1 模块功能

池化操作和激活操作的本质目的是为了降低卷积神经网络的运算量，而实际中在卷积操作过程中，这些操作显然是必要的，尽管上述操作会牺牲掉数据的精度和完备性，但表现在最终的应用效果上并不是那么明显，就是说这样一种取舍是十分必要的。池化一般有平均值池化、最大值池化等，平均值池化为的是做均值处理，在图像处理中常用到低通滤波操作，最大值池化类似图像处理中的锐化操作。

本设计中使用的是最大值池化，模板为2×2大小，故再输出的32×32的数据中，经过池化操作会变成16×16=256的输出ofm数据，共计128输出通道为128×256个8bit数据。

激活操作，实际上是利用函数对输出数据进行操作，自变量就是输入的池化后的数据，输出数据就是最终待数据位宽处理的数据，本设计中采用的是max线性激活函数，顾名思义就是将输入的负数进行归0处理，正数和0按照正比例1:1跟随输出。进过上述操作后，数据的归一性更加突出，即输出数据置存在0和正数的情况。

3.8.2 接口定义

如下图所示，为池化和激活操作模块的symbol示意图。

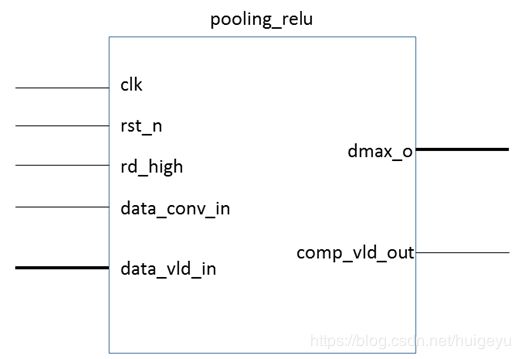
该模块相关输入输出接口的说明详见表3-8-1。

3.8.3 实现方案

池化的实现较激活实现较难，由于数据是串行的，这里引入一种思路：因为池化操作是用模板去框选输入数据，每次的大小是2×2，步进是2，这与之前的卷积操作的模板框选是不同的。

因为是串行的，最基本的思路是先把数据串行存入ram中，而后再讲对应位置取出进行max操作，这实际上与卷积的模板操作类似。但是，这儿，事先如果用ram存储数据的话，会造成空间的浪费;

故而，采用另一种思路，只采用34个大小的ram，按照打拍刷新输入数据的方式，每2次则进行一次模板框选，在每一输出通道出事34个地址时，需要进行34时钟打拍的初始化操作，那么便能够同样以串行输出的方式得到数据。这值得注意的是，按照上述思路，需要注意，是多余的数据会产生，因为按照串行2拍进行一次操作，那么1024个数据则需要（1024-34）/2+1=496个数据，实际上数据应该是每隔16个数据才是有效数据，这里为了操作简便，直接在顶层sv模块里面进行操作。

最终，得到128×256的输出ofm数据，格式按照给定的数据模板打印到TXT上。

3.9 截位模块

3.9.1 模块功能

该模块实现了对数据的高位截取和饱和处理。

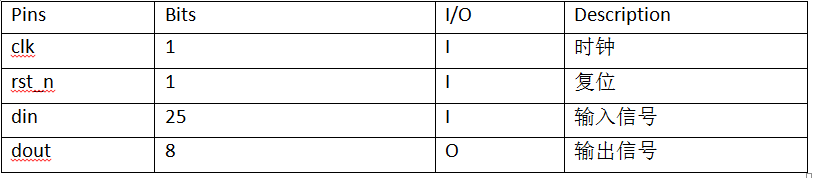
3.9.2 接口定义

下图3-9-1所示，为单通道全卷积模块symbol示意图。

以下通过表3-9-1，对该模块的输入输出端口进行介绍。

3.9.3 实现方案

通过参数传递的方式，该模块可以实现对任意位宽数据的任意位高位截取和以及任意位饱和处理，同时该模块均采用组合逻辑。

高位截取采用四舍五入的方式，假设要扔掉din的低9位，则需要判定din的第九位是否为1。如果为1，表示扔掉的数据部分大于等于2^8，满足进位条件；如果为0，则不进位。

饱和处理过程需要扔掉高位，假设要扔掉round[15:0]高8位（round[15:0]为din[24:0]四舍五入后的结果），则判断round的高16位是否全为0。若全为0，则直接舍去高8位；若不全为0，则结果等于8’h7f。

3.10 总体验证平台

（要求介绍用UVM搭建的testbench，以及各组件结构图）

3.11 验证组件介绍

DUT：本题目的所有模块的RTL代码；
in_if、out_if：功能模块TOP.v涉及到的端口，将捆绑在一起，并定义为interface类型。包括时钟信号线、置位信号线、64根ifm接收信号线、64根weight接收信号线、1根bias接收信号线；
Driver：将激励通过vif传输给DUT； Sequence：产生测试所需要的激励；
Sequencer：接收sequence产生的激励，并通过export传输给Driver；
i_monitor：通过in_if接收输入的激励； o_monitor：通过out_if接收DUT的输出结果；
i_agent：将Sequencer、Driver、i_monitor打包在一起；
o_agent：将o_monitor打个包，放在更高的一个抽象层；
Port、Export、FIFO：通信接口，辅助连接ENV层次下，各个模块的连接；
model：DUT的理想功能模块，其代表着DUT需要实现的目标功能；
Scoreboard：接收来自o_agent和理想模块model的数据，并进行比对，通过查看计分板我们可以实现验证DUT的目的，对出现的错误进行Debug。

以上所有组件结合起来，就是整个测试平台。

3.12 Testplan方案

测试方案分两种，一是随机测试，即输入矩阵、卷积核以及偏置均随机产生；二是极端测试，考虑到数据均为有符号数，所有极端状况分三种，分别是最小值（负数）、0、最大值（正数），又因为输入分为输入矩阵、卷积核以及偏置，所有极端测试共有27种情况。
综上，测试方案有两种，共28种情况。

3.13 仿真结果

如下图3-12-1，为整体输出的仿真结果，数据基本上与模板一致。

总结：
本次设计完美地体现学习和实践的结合。从最开始的对卷积网络算的不了解，到慢慢的一点一点了解，再到最后通过RTL代码实现。整个过程对卷积网络的学习，提高了知识面的广度，以及RTL代码实现，增强了知识面的深度，广度与深度的结合，得到了一个深刻以及全面的学习。此外，通过RTL代码对大量数据的处理，是之前不曾接触到的，无形中丰富了自己coding经验和能力。

再来就是设计结果，由于算法原因，最终是单通道串行输出，因为这样设计，在中间的算法过程中可以节省很多存储空间，这也是牺牲输出通道来换取存储空间的结果。整体算法还有可提升空间，比对最终结果，对中间数据的位宽处理还可以更细化，以提升处理速度，同时在数据存储方案上，看是否还有存在更小内存。