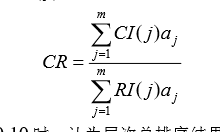数学建模之层次分析实例含代码

参考书籍《数学建模算法与应用》

 一，层次分析法的步骤

（i）建立递阶层次结构模型；

（ii）构造出各层次中的所有判断矩阵。

  关于如何确定 aij 的值，Saaty 等建议引用数字 1~9 及其倒数作为标度。表 1 列出 了 1~9 标度的含义： 

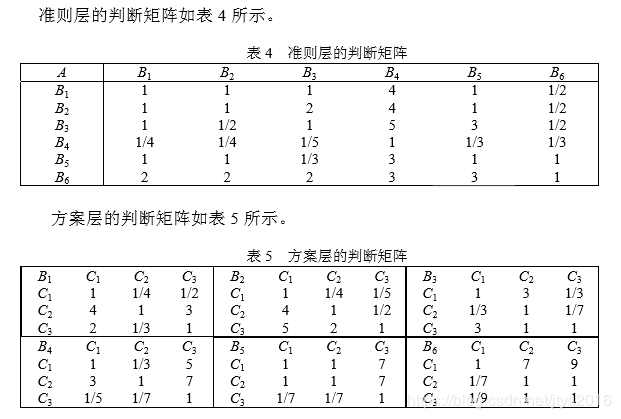
 根据图2层次结构模型构造了准则层对目标层的判断矩阵（成对比较阵），方案层对准则层的判断矩阵，如下：

 

A，B1，B2，B3 ，B4， B5， B6称正互反矩阵。 

（iii）层次单排序及一致性检验。

       n阶正互反矩阵 A为一致矩阵当且仅当其最大特征根 n =max λ，且当正互反矩阵 A非一致时，必有 n >max λ。我们可以由 max λ是否等于n 来检验判断矩阵 A是否为一致矩阵。

       由于特征根连续地依赖于 aij ，故 max λ比n大得越多， A的非一致性程度也就越严重，max λ对应的标准化特征向量也就越不能真实地反映出所占的比重。因此，对决策者提供的判断矩阵有必要作一次一致性检验，以决定是否能接受它。

 

简而言之就是对比较阵计算最大特征根和特征向量，作一致性检验，若通过则特征向量为权向量 。

（iv）层次总排序及一致性检验。 

       对层次总排序也需作一致性检验，检验仍象层次总排序那样由高层到低层逐层进 行。这是因为虽然各层次均已经过层次单排序的一致性检验，各成对比较判断矩阵都 已具有较为满意的一致性。但当综合考察时，各层次的非一致性仍有可能积累起来， 引起最终分析结果较严重的非一致性。 

    

 

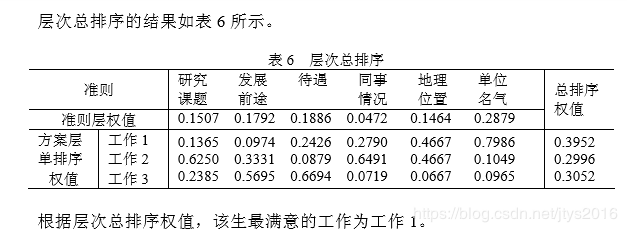
 将多层的权向量组合课作为决策依据，层次总排序如下：

工作1对目标的组合权重为0.1365*0.1507+0.0974*0.1792+···+0.7986*0.2879=0.3952 

工作2对目标的组合权重为0.625*0.1507+0.3331*0.1792+···+0,1049*0.2879=0.2996

同理工作3

二，代码

clc,clear 
fid=fopen('cengci.txt','r');  
n1=6;n2=3; a=[]; 
for i=1:n1    
    tmp=str2num(fgetl(fid));  %fgetl从这个文件中读取一行数据并丢弃其中的换行符。
    a=[a;tmp]; %读准则层判断矩阵 
end
for i=1:n1     
    str1=char(['b',int2str(i),'=[];']);                %int2str()数值i四舍五入后转变成字符  
    str2=char(['b',int2str(i),'=[b',int2str(i),';tmp];']); %char()将中括号内的三个字符串拼成一个字符串并赋给str1 
    eval(str1);     %括号内的字符串视为语句并运行
    for j=1:n2         
        tmp=str2num(fgetl(fid));         
        eval(str2); %读方案层的判断矩阵     
    end
end
ri=[0,0,0.58,0.90,1.12,1.24,1.32,1.41,1.45]; %一致性指标 
%准则层对目标层的一致性检验 包括特征值和特征向量
[x,y]=eig(a);  %x为特征向量， y为特征值                              
lamda=max(diag(y)); %最大特征值
num=find(diag(y)==lamda); 
w0=x(:,num)/sum(x(:,num)); %最大特征值对应的特征向量（权向量）
cr0=(lamda-n1)/(n1-1)/ri(n1) %cr=ci/ri 若cr<0.1则通过一致性检验

%方案层对准则层的一致性检验
for i=1:n1      
    [x,y]=eig(eval(char(['b',int2str(i)])));     
    lamda=max(diag(y));     
    num=find(diag(y)==lamda);    
    w1(:,i)=x(:,num)/sum(x(:,num));     
    cr1(i)=(lamda-n2)/(n2-1)/ri(n2); 
end
w0, w1, cr1, ts=w1*w0, cr=cr1*w0 %ts为方案层对目标的组合权重 比较大小再确定方案，cr为准测层总排序随机一致性比例

cengci.txt数据如下：

 

三，结果