FVM in CFD 学习笔记_第13章_时域离散:瞬态项
学习自F. Moukalled, L. Mangani, M. Darwish所著The Finite Volume Method in Computational Fluid Dynamics - An Advanced Introduction with OpenFOAM and Matlab
Chapter 13 Temporal Discretization: The Transient Term
前面章节的讨论中均假设是稳态条件,所以无需对瞬态项进行离散。如果考虑瞬态现象的话,则相当于给问题增加了一个新的维度。然而,由于瞬态项的性质是抛物型的,故而不需要再额外定义时间域上的场,即,不像在空间域上需要用 ϕ i , i = 1 , 2 , . . . , N \phi_i,i=1,2,...,N ϕi,i=1,2,...,N那样子来离散节点值。一般来说,瞬态项的离散只需要额外存储一到两个时间层上的变量场即可,由所选择格式的数值精度而定。与稳态问题的另一个不同点是,瞬态系统是用时间步长推进方式来模拟的,即,以 t = t 0 t=t_0 t=t0时刻的初始条件开始,求解算法向前推进并找到 t 1 = t 0 + Δ t 1 t_1=t_0+\Delta t_1 t1=t0+Δt1时刻的解,这个找到的解再作为初始条件去找寻 t 2 = t 1 + Δ t 2 t_2=t_1+\Delta t_2 t2=t1+Δt2时刻的解,该过程不断重复直到达到所需的时刻为止。本章的重点是瞬态项离散的技术,将展示两种发展瞬态格式的方法。其一是使用Taylor展开来把瞬态项展开成节点值的形式,这在有限差分方法中非常奏效;其二是有限体积方法中常用的伪时间单元方法,和在对流项中的伪节点非常类似。将展示一些瞬态格式,并讨论它们的特性。
1 引言
对于瞬态模拟而言,控制方程的离散是在空间域和时间域上进行的。空间域上的空间离散和稳态问题一样,时间离散则要设置一个时间坐标轴,沿着该坐标轴来计算瞬态项的导数(有限差分方法)或积分(有限体积方法)值。
一般而言,某个变量 ϕ \phi ϕ的瞬态特性的表达式,或其时间演化,是由下述形式的方程控制的
∂ ( ρ ϕ ) ∂ t + L ( ϕ ) = 0 \frac{\partial (\rho \phi)}{\partial t}+L(\phi)=0 ∂t∂(ρϕ)+L(ϕ)=0
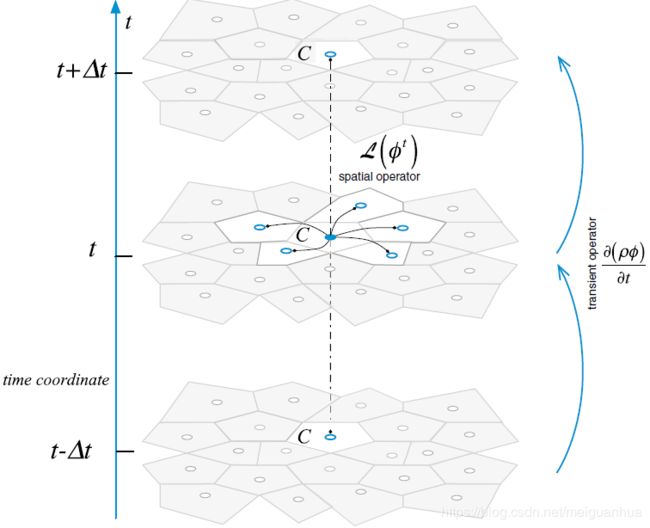
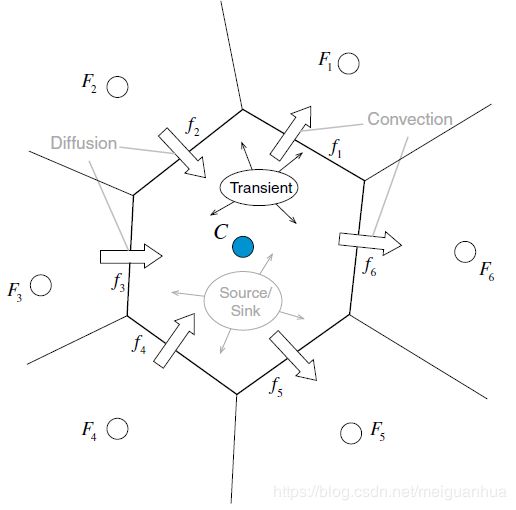
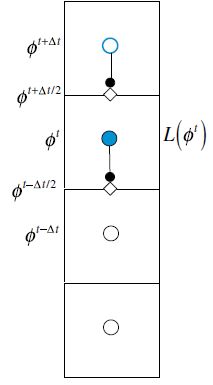
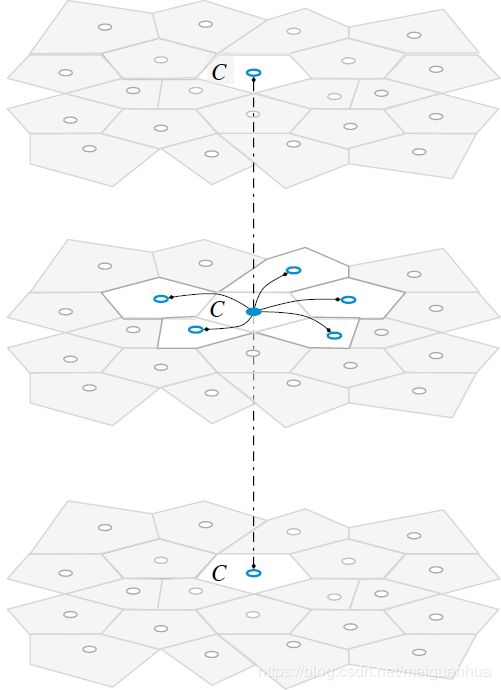
其中 L ( ϕ ) L(\phi) L(ϕ)为空间算子,其包含了所有的非瞬态项(扩散项、对流项、源项,等), ∂ ( ρ ϕ ) / ∂ t {\partial (\rho \phi)}/{\partial t} ∂(ρϕ)/∂t为瞬态算子,两者如下图所示。
在单元 C C C上对上式做积分,得
∫ V C ∂ ( ρ ϕ ) ∂ t d V + ∫ V C L ( ϕ ) d V = 0 \int_{V_C}\frac{\partial (\rho \phi)}{\partial t}dV+\int_{V_C}L(\phi)dV=0 ∫VC∂t∂(ρϕ)dV+∫VCL(ϕ)dV=0
空间离散后,变为
∂ ( ρ C ϕ C ) ∂ t V C + L ( ϕ C t ) = 0 \frac{\partial (\rho_C \phi_C)}{\partial t}V_C+L(\phi_C^t)=0 ∂t∂(ρCϕC)VC+L(ϕCt)=0
其中 V C V_C VC为离散单元的体积, L ( ϕ C t ) L(\phi_C^t) L(ϕCt)为空间算子在某参考时刻 t t t的离散形式,可写成如下代数方程
L ( ϕ C t ) = a C ϕ C t + ∑ F ∼ N B ( C ) a F ϕ F t − b C L(\phi_C^t)=a_C\phi_C^t+\sum_{F\sim NB(C)}a_F\phi_F^t-b_C L(ϕCt)=aCϕCt+F∼NB(C)∑aFϕFt−bC
在上上式中,当 t → ∞ t\rightarrow\infin t→∞时其变为稳态离散方程。通过时间推进也能达到稳态,即, ϕ C t + Δ t = ϕ C t \phi_C^{t+\Delta t}=\phi_C^t ϕCt+Δt=ϕCt。这保证了瞬态问题在到达稳态时所获得的解,和直接由稳态问题求得的解,是一样的。
在瞬态项的离散中,最经典的法子是用有限差分法的思想,把 ∂ ( ρ ϕ ) / ∂ t {\partial (\rho \phi)}/{\partial t} ∂(ρϕ)/∂t做Taylor级数展开,得到用离散点的值所表示的导数项形式。在本章中,将展示另一种与有限体积方法更为契合的方法,对 ∂ ( ρ ϕ ) / ∂ t {\partial (\rho \phi)}/{\partial t} ∂(ρϕ)/∂t在时间单元上做积分,并转化为面通量的形式,这和对流格式的处理方法很像,只是现在离散是沿着时间轴进行的。
2 有限差分方法
如图,在瞬态空间中的网格是结构化的,所以对瞬态项使用有限差分方法是非常稀松平常的操作。在该方法中,空间算子 L ( ϕ ) L(\phi) L(ϕ)是在时刻 t t t离散的,而瞬态偏导数则可用时刻 t t t的Taylor展开而推导出不同的瞬态格式,其中的一些格式呈现如下。
2.1 前向Euler格式(Forward Euler Scheme)
为了估算瞬态项,所推导量的Taylor展开需要指定时间方向。这里,展开是针对时间向前进行的。对某函数 T T T,其在 t + Δ t t+\Delta t t+Δt时刻的值,可用其在时刻 t t t的值和导数值做Taylor级数展开,如下
T ( t + Δ t ) = T ( t ) + ∂ T ( t ) ∂ t Δ t + ∂ 2 T ( t ) ∂ t 2 Δ t 2 2 ! + . . . T(t+\Delta t)=T(t)+\frac{\partial T(t)}{\partial t}\Delta t+\frac{\partial^2 T(t)}{\partial t^2}\frac{\Delta t^2}{2!}+... T(t+Δt)=T(t)+∂t∂T(t)Δt+∂t2∂2T(t)2!Δt2+...
截去二阶以上项,得到
∂ T ( t ) ∂ t = T ( t + Δ t ) − T ( t ) Δ t + O ( Δ t ) \frac{\partial T(t)}{\partial t}=\frac{T(t+\Delta t)-T(t)}{\Delta t}+O(\Delta t) ∂t∂T(t)=ΔtT(t+Δt)−T(t)+O(Δt)
只有一阶精度,把上式中的 T T T替换成 ( ρ ϕ ) (\rho\phi) (ρϕ),并代入到 ∂ ( ρ C ϕ C ) ∂ t V C + L ( ϕ C t ) = 0 \frac{\partial (\rho_C \phi_C)}{\partial t}V_C+L(\phi_C^t)=0 ∂t∂(ρCϕC)VC+L(ϕCt)=0,离散方程变为
( ρ C ϕ C ) t + Δ t − ( ρ C ϕ C ) t Δ t V C + L ( ϕ C t ) = 0 \frac{(\rho_C \phi_C)^{t+\Delta t}-(\rho_C \phi_C)^t}{\Delta t}V_C+L(\phi_C^t)=0 Δt(ρCϕC)t+Δt−(ρCϕC)tVC+L(ϕCt)=0

该瞬态格式如上图所示,计算 t + Δ t t+\Delta t t+Δt时刻的 ( ρ C ϕ C ) (\rho_C \phi_C) (ρCϕC)是不需要求解方程组系统的。因为所有的空间项都是在旧时刻 t t t上衡量的,所以 t + Δ t t+\Delta t t+Δt时刻的 ϕ C \phi_C ϕC可直接由上个时间步的值显式算出。这样的格式属于显式瞬态格式。显式瞬态格式的主要特点是通过在时域推进便可获得解,而无需在每个时间层求解方程组系统。这样一来,求解效率非常高,且对计算网格的并行处理十分方便。然而鲜有商业软件采用该方法,因为其重大缺陷就是时间步长 Δ t \Delta t Δt极为受限,这将在下一小节详细展开。
把空间算子的离散代数方程代入到上式,可得完整的代数方程为
a C t + Δ t ϕ C t + Δ t + a C t ϕ C t = b C − ( a C ϕ C t + ∑ F ∼ N B ( C ) a F ϕ F t ) a_C^{t+\Delta t} \phi_C^{t+\Delta t} + a_C^t \phi_C^t = b_C-\left(a_C\phi_C^t+\sum_{F\sim NB(C)}a_F\phi_F^t\right) aCt+ΔtϕCt+Δt+aCtϕCt=bC−⎝⎛aCϕCt+F∼NB(C)∑aFϕFt⎠⎞
其中
a C t + Δ t = ρ C t + Δ t V C Δ t a C t = − ρ C t V C Δ t \begin{aligned} a_C^{t+\Delta t} &= \frac{\rho_C ^{t+\Delta t}V_C}{\Delta t} \\ a_C^t &= -\frac{\rho_C^tV_C}{\Delta t} \end{aligned} aCt+ΔtaCt=ΔtρCt+ΔtVC=−ΔtρCtVC
在上述方程中, a C t + Δ t a_C^{t+\Delta t} aCt+Δt和 a C t a_C^t aCt为对角系数,源自于瞬态项的离散, ϕ C t + Δ t \phi_C^{t+\Delta t} ϕCt+Δt和 ϕ C t \phi_C^t ϕCt为时间层 t + Δ t t+\Delta t t+Δt和 t t t上的值,而 a C a_C aC、 a F a_F aF、 b C b_C bC则是空间离散后的系数。
为了简化标记,在本章中,前一个时间步的变量值用上标 ∘ ^\circ ∘标记,前两个时间步的变量值用上标 ∘ ∘ ^{\circ\circ} ∘∘标记,若是没有上标,则表示当前时间步的变量值,除了在非定常项中乘到 ϕ C \phi_C ϕC上的系数是用上标 ∙ ^\bullet ∙来标记的。基于这些标记,上式写作
a C ∙ ϕ C + a C ∘ ϕ C ∘ = b C − ( a C ϕ C ∘ + ∑ F ∼ N B ( C ) a F ϕ F ∘ ) a_C^{\bullet} \phi_C + a_C^\circ \phi_C^\circ = b_C-\left(a_C\phi_C^\circ+\sum_{F\sim NB(C)}a_F\phi_F^\circ\right) aC∙ϕC+aC∘ϕC∘=bC−⎝⎛aCϕC∘+F∼NB(C)∑aFϕF∘⎠⎞
其中
a C ∙ = ρ C V C Δ t a C ∘ = − ρ C ∘ V C Δ t \begin{aligned} a_C^{\bullet} &= \frac{\rho_C V_C}{\Delta t} \\ a_C^\circ &= -\frac{\rho_C^\circ V_C}{\Delta t} \end{aligned} aC∙aC∘=ΔtρCVC=−ΔtρC∘VC
改写为如下形式
ϕ C = b C − [ ( a C + a C ∘ ) ϕ C ∘ + ∑ F ∼ N B ( C ) a F ϕ F ∘ ] a C ∙ \phi_C = \frac{b_C-\left[(a_C+a_C^\circ)\phi_C^\circ+\displaystyle\sum_{F\sim NB(C)}a_F\phi_F^\circ\right]}{a_C^{\bullet}} ϕC=aC∙bC−⎣⎡(aC+aC∘)ϕC∘+F∼NB(C)∑aFϕF∘⎦⎤
显然,当前时间步的 ϕ \phi ϕ值是由显式关系算出来的,不需要求解方程组系统。
2.2 前向Euler格式的稳定性
数值格式的收敛性和稳定性最初是由Courant、Friedrichs、Lewy所探究的,他们表明,为了让差分方程的解收敛到原偏微分方程的解,数值格式中必须用到影响解的初始数据所包含的所有信息。该要求随后就变成了著名的CFL条件。
实际上,CFL条件可以被简单解释为,把系数所要满足的基本规则之一,即,反符号准则,扩展成把瞬态系数也包含在内。这样,正如 ϕ F \phi_F ϕF是 ϕ C \phi_C ϕC的“空间”邻居, ϕ C ∘ \phi_C^\circ ϕC∘也是 ϕ C \phi_C ϕC的“时间”邻居,那么反符号准则对他俩应该平等适用。注意对角线系数现在是 a C ∙ a_C^\bullet aC∙,其“时间”邻居的系数是 ( a C + a C ∘ ) (a_C+a_C^\circ) (aC+aC∘),反符号准则变为
a C + a C ∘ ≤ 0 a_C+a_C^\circ\le0 aC+aC∘≤0
2.2.1 瞬态-对流情况的稳定性
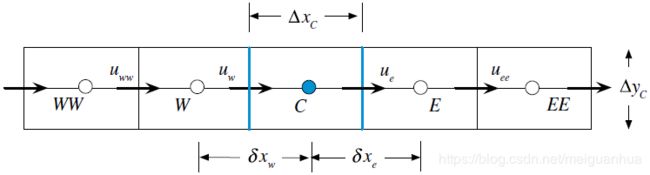
如上图,对于一维纯对流问题,流动方向向右,使用迎风格式把变量插值到单元面上去,则单元 C C C的离散方程中的系数 a C a_C aC和 a C ∘ a_C^\circ aC∘为
a C = m ˙ e ∘ = ρ C ∘ u C ∘ Δ y C a C ∘ = − ρ C ∘ V C Δ t = − ρ C ∘ Δ x C Δ y C Δ t \begin{aligned} a_C&=\dot m_e^\circ=\rho_C^\circ u_C^\circ \Delta y_C \\ a_C^\circ&=-\frac{\rho_C^\circ V_C}{\Delta t}=-\frac{\rho_C^\circ \Delta x_C \Delta y_C}{\Delta t} \end{aligned} aCaC∘=m˙e∘=ρC∘uC∘ΔyC=−ΔtρC∘VC=−ΔtρC∘ΔxCΔyC
因此,CFL条件为
a C + a C ∘ ≤ 0 ⇒ ρ C ∘ u C ∘ Δ y C − ρ C ∘ Δ x C Δ y C Δ t ≤ 0 a_C+a_C^\circ\le0 \Rightarrow \rho_C^\circ u_C^\circ \Delta y_C-\frac{\rho_C^\circ \Delta x_C \Delta y_C}{\Delta t}\le0 aC+aC∘≤0⇒ρC∘uC∘ΔyC−ΔtρC∘ΔxCΔyC≤0
即
Δ t ≤ Δ x C u C ∘ \Delta t\le\frac{\Delta x_C}{u_C^\circ} Δt≤uC∘ΔxC
对于对流控制的流动,定义CFL数为
C F L c o n v = ∣ v C ∘ ∣ Δ t Δ x C CFL^{conv}=\frac{|\bold v_C^\circ|\Delta t}{\Delta x_C} CFLconv=ΔxC∣vC∘∣Δt
这意味着为了数值稳定性,CFL数应该满足
C F L c o n v ≤ 1 CFL^{conv}\le1 CFLconv≤1
2.2.2 瞬态-扩散情况的稳定性
对于纯扩散问题,CFL数的表达式是不同的。因此,分析如上图所示的一维纯扩散问题。
使用线性插值廓线,单元 C C C的离散方程中的系数 a C a_C aC和 a C ∘ a_C^\circ aC∘为
a C = Γ e ϕ Δ y C δ x e + Γ w ϕ Δ y C δ x w a C ∘ = − ρ C ∘ V C Δ t = − ρ C ∘ Δ x C Δ y C Δ t \begin{aligned} a_C&=\frac{\Gamma_e^\phi \Delta y_C}{\delta x_e} + \frac{\Gamma_w^\phi \Delta y_C}{\delta x_w} \\ a_C^\circ&=-\frac{\rho_C^\circ V_C}{\Delta t}=-\frac{\rho_C^\circ \Delta x_C \Delta y_C}{\Delta t} \end{aligned} aCaC∘=δxeΓeϕΔyC+δxwΓwϕΔyC=−ΔtρC∘VC=−ΔtρC∘ΔxCΔyC
因此,CFL条件需要
a C + a C ∘ ≤ 0 ⇒ Γ e ϕ Δ y C δ x e + Γ w ϕ Δ y C δ x w − ρ C ∘ Δ x C Δ y C Δ t ≤ 0 a_C+a_C^\circ\le0 \Rightarrow \frac{\Gamma_e^\phi \Delta y_C}{\delta x_e} + \frac{\Gamma_w^\phi \Delta y_C}{\delta x_w}-\frac{\rho_C^\circ \Delta x_C \Delta y_C}{\Delta t}\le0 aC+aC∘≤0⇒δxeΓeϕΔyC+δxwΓwϕΔyC−ΔtρC∘ΔxCΔyC≤0
即
Δ t ≤ ρ C ∘ Δ x C Γ e ϕ δ x e + Γ w ϕ δ x w \Delta t\le\frac{\rho_C^\circ\Delta x_C}{\dfrac{\Gamma_e^\phi}{\delta x_e} + \dfrac{\Gamma_w^\phi}{\delta x_w}} Δt≤δxeΓeϕ+δxwΓwϕρC∘ΔxC
若网格均匀,且扩散系数为常数,则上式变为
Δ t ≤ ρ C ∘ ( Δ x C ) 2 2 Γ C ϕ \Delta t\le\frac{\rho_C^\circ(\Delta x_C)^2}{2\Gamma_C^\phi} Δt≤2ΓCϕρC∘(ΔxC)2
对于扩散控制的问题,定义CFL数为
C F L d i f f = Γ C ϕ Δ t ρ C ∘ ( Δ x C ) 2 CFL^{diff}=\frac{\Gamma_C^\phi\Delta t}{\rho_C^\circ(\Delta x_C)^2} CFLdiff=ρC∘(ΔxC)2ΓCϕΔt
这意味着为了数值稳定性,CFL数应该满足
C F L d i f f ≤ 1 2 CFL^{diff}\le \frac{1}{2} CFLdiff≤21
2.2.3 瞬态-对流-扩散情况的稳定性
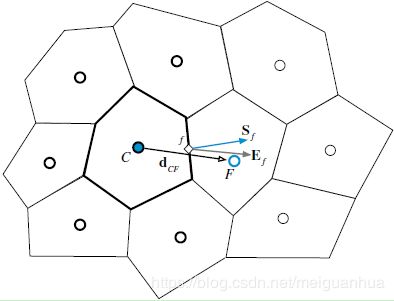
对于多维非定常对流扩散问题,基于上一章(第12章)的推导,系数 a C a_C aC和 a C ∘ a_C^\circ aC∘为
a C = ∑ f ∼ n b ( C ) ( Γ f ϕ E f d C F + ∣ ∣ m ˙ f ∘ , 0 ∣ ∣ ) a C ∘ = − ρ C ∘ V C Δ t \begin{aligned} a_C&=\sum_{f\sim nb(C)}\left( \Gamma_f^\phi\frac{E_f}{d_{CF}} + ||\dot m_f^\circ,0|| \right) \\ a_C^\circ&=-\frac{\rho_C^\circ V_C}{\Delta t} \end{aligned} aCaC∘=f∼nb(C)∑(ΓfϕdCFEf+∣∣m˙f∘,0∣∣)=−ΔtρC∘VC
CFL条件变为
a C + a C ∘ ≤ 0 ⇒ ∑ f ∼ n b ( C ) ( Γ f ϕ E f d C F + ∣ ∣ m ˙ f ∘ , 0 ∣ ∣ ) − ρ C ∘ V C Δ t ≤ 0 a_C+a_C^\circ\le0 \Rightarrow \sum_{f\sim nb(C)}\left( \Gamma_f^\phi\frac{E_f}{d_{CF}} + ||\dot m_f^\circ,0|| \right) -\frac{\rho_C^\circ V_C}{\Delta t} \le0 aC+aC∘≤0⇒f∼nb(C)∑(ΓfϕdCFEf+∣∣m˙f∘,0∣∣)−ΔtρC∘VC≤0
即如下对时间步长的限制关系
Δ t ≤ ρ C ∘ V C ∑ f ∼ n b ( C ) ( Γ f ϕ E f d C F + ∣ ∣ m ˙ f ∘ , 0 ∣ ∣ ) \Delta t \le \frac{\rho_C^\circ V_C}{\displaystyle\sum_{f\sim nb(C)}\left( \Gamma_f^\phi\frac{E_f}{d_{CF}} + ||\dot m_f^\circ,0|| \right) } Δt≤f∼nb(C)∑(ΓfϕdCFEf+∣∣m˙f∘,0∣∣)ρC∘VC
上式通常是显式瞬态格式的稳定性要求,实际上,之前对一维区域的纯对流和纯扩散的条件,可以视作是上式的特例。比如一维扩散问题,有均匀网格单元尺度 Δ x \Delta x Δx,常密度 ρ \rho ρ,均匀扩散系数 Γ ϕ \Gamma^\phi Γϕ,上式变为
Δ t ≤ ρ C ∘ V C ∑ f ∼ n b ( C ) ( Γ f ϕ E f d C F + ∣ ∣ m ˙ f ∘ , 0 ∣ ∣ ) = ρ C ∘ Δ x C Δ y C ( Γ e ϕ + Γ w ϕ ) Δ y C Δ x C = ρ C ∘ ( Δ x C ) 2 2 Γ C ϕ \Delta t \le \frac{\rho_C^\circ V_C} {\displaystyle\sum_{f\sim nb(C)}\left( \Gamma_f^\phi \frac{E_f}{d_{CF}} + ||\dot m_f^\circ,0|| \right) }= \frac{\rho_C^\circ \Delta x_C \Delta y_C} {(\Gamma_e^\phi+\Gamma_w^\phi) \dfrac{\Delta y_C}{\Delta x_C} }= \frac{\rho_C^\circ(\Delta x_C)^2}{2\Gamma_C^\phi} Δt≤f∼nb(C)∑(ΓfϕdCFEf+∣∣m˙f∘,0∣∣)ρC∘VC=(Γeϕ+Γwϕ)ΔxCΔyCρC∘ΔxCΔyC=2ΓCϕρC∘(ΔxC)2
而对于纯对流的一维问题,使用迎风格式离散对流项,流体从左向右流动,则其变为了
Δ t ≤ ρ C ∘ V C ∑ f ∼ n b ( C ) ( Γ f ϕ E f d C F + ∣ ∣ m ˙ f ∘ , 0 ∣ ∣ ) = ρ C ∘ Δ x C Δ y C ρ C ∘ u C ∘ Δ y C = Δ x C u C ∘ \Delta t \le \frac{\rho_C^\circ V_C} {\displaystyle\sum_{f\sim nb(C)}\left( \Gamma_f^\phi \frac{E_f}{d_{CF}} + ||\dot m_f^\circ,0|| \right) }= \frac{\rho_C^\circ \Delta x_C \Delta y_C}{\rho_C^\circ u_C^\circ \Delta y_C }=\frac{\Delta x_C}{u_C^\circ} Δt≤f∼nb(C)∑(ΓfϕdCFEf+∣∣m˙f∘,0∣∣)ρC∘VC=ρC∘uC∘ΔyCρC∘ΔxCΔyC=uC∘ΔxC
稳定性限制条件是严格的,且限制性很强,它迫使在求解瞬态问题时采用非常小的时间步长。这样做的后果是,尽管每个时间步的计算消耗很小(相比于每个时间步要求解方程组系统而言),然而CFL条件使得必须求解很多时间步才能推进到终了时刻。这样一来,每个时间步减少的计算量的优势就毫无意义了,因为反而需要更多的时间步来求解了。此外,CFL条件表明,如果通过减小网格尺度来提高空间精度的话,那么会更进一步地减小为保证稳定性所能使用的最大时间步长。
下面会看到,这样的限制条件对于隐式格式来说并不存在,因为其瞬态项的符号总是合适的。
2.3 后向Euler格式(Backward Euler Scheme)
为了推出后向Euler格式,把在时刻 t − Δ t t-\Delta t t−Δt的函数 T T T值用在时刻 t t t的函数 T T T值做Taylor级数展开,有
T ( t − Δ t ) = T ( t ) − ∂ T ( t ) ∂ t Δ t + ∂ 2 T ( t ) ∂ t 2 Δ t 2 2 ! + . . . T(t-\Delta t)=T(t)-\frac{\partial T(t)}{\partial t}\Delta t+\frac{\partial^2 T(t)}{\partial t^2}\frac{\Delta t^2}{2!}+... T(t−Δt)=T(t)−∂t∂T(t)Δt+∂t2∂2T(t)2!Δt2+...
整理后,有
∂ T ( t ) ∂ t = T ( t ) − T ( t − Δ t ) Δ t + ∂ 2 T ( t ) ∂ t 2 Δ t 2 + . . . \frac{\partial T(t)}{\partial t}=\frac{T(t)-T(t-\Delta t)}{\Delta t}+\frac{\partial^2 T(t)}{\partial t^2}\frac{\Delta t}{2}+... ∂t∂T(t)=ΔtT(t)−T(t−Δt)+∂t2∂2T(t)2Δt+...
把上式中的 T T T替换成 ( ρ ϕ ) (\rho\phi) (ρϕ),并代入到 ∂ ( ρ C ϕ C ) ∂ t V C + L ( ϕ C t ) = 0 \frac{\partial (\rho_C \phi_C)}{\partial t}V_C+L(\phi_C^t)=0 ∂t∂(ρCϕC)VC+L(ϕCt)=0,离散方程变为
( ρ C ϕ C ) t − ( ρ C ϕ C ) t − Δ t Δ t V C + L ( ϕ C t ) = 0 \frac{(\rho_C \phi_C)^{t}-(\rho_C \phi_C)^{t-\Delta t}}{\Delta t}V_C+L(\phi_C^t)=0 Δt(ρCϕC)t−(ρCϕC)t−ΔtVC+L(ϕCt)=0
接下来,引入空间离散项的代数方程,并根据之前设置的上标,瞬态标量方程的完整代数形式为
( a C ∙ + a C ) ϕ C + ∑ F ∼ N B ( C ) a F ϕ F = b C − a C ∘ ϕ C ∘ (a_C^{\bullet}+a_C) \phi_C +\sum_{F\sim NB(C)}a_F\phi_F =b_C-a_C^\circ\phi_C^\circ (aC∙+aC)ϕC+F∼NB(C)∑aFϕF=bC−aC∘ϕC∘
其中
a C ∙ = ρ C V C Δ t a C ∘ = − ρ C ∘ V C Δ t \begin{aligned} a_C^{\bullet} &= \frac{\rho_C V_C}{\Delta t} \\ a_C^\circ &= -\frac{\rho_C^\circ V_C}{\Delta t} \end{aligned} aC∙aC∘=ΔtρCVC=−ΔtρC∘VC
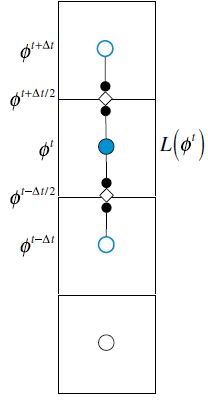
其架构如下图所示,显然,空间算子是在和新时间系数相同的时间层上计算的,所以,求解新时刻的 ϕ \phi ϕ场是需要求解方程组系统的。这种需要求解方程组系统的解法便是隐式格式。
从上式中可以看出, a C a_C aC和 a C ∘ a_C^\circ aC∘的符号是相反的(满足反号准则,即对角系数和邻居系数符号是相反的),这样便可保证 ϕ C \phi_C ϕC是由其 当前时间步的空间邻近点的值 和 前一时间步 t − Δ t t-\Delta t t−Δt的时间邻近点的值 所限定的。这也意味着该格式总是稳定的,而不管用的是何种时间步长,从而可以用很大的时间步长向前快速推进。纵然如此,其并非是理想格式,因为其精度较低,这种格式获得的解精确性差,除非用很小的时间步长才好,这让其使用起来颇为尴尬。若采用大时间步长来提高计算效率,则获得的解精度很差。若使用小时间步长来获得精确解,则计算效率会非常低下。
2.4 Crank-Nicolson格式
在Crank-Nicolson格式中,为了获得瞬态项更加精确的近似,采用了在 t − Δ t t-\Delta t t−Δt时刻的函数 T T T值和在 t + Δ t t+\Delta t t+Δt时刻的函数 T T T值的展开形式,同样是用 t t t时刻的量来展开的,即
T ( t + Δ t ) = T ( t ) + ∂ T ( t ) ∂ t Δ t + ∂ 2 T ( t ) ∂ t 2 Δ t 2 2 ! + ∂ 3 T ( t ) ∂ t 3 Δ t 3 3 ! + . . . T ( t − Δ t ) = T ( t ) − ∂ T ( t ) ∂ t Δ t + ∂ 2 T ( t ) ∂ t 2 Δ t 2 2 ! − ∂ 3 T ( t ) ∂ t 3 Δ t 3 3 ! + . . . \begin{aligned} T(t+\Delta t)=T(t)+\frac{\partial T(t)}{\partial t}\Delta t+\frac{\partial^2 T(t)}{\partial t^2}\frac{\Delta t^2}{2!}+\frac{\partial^3 T(t)}{\partial t^3}\frac{\Delta t^3}{3!}+... \\ T(t-\Delta t)=T(t)-\frac{\partial T(t)}{\partial t}\Delta t+\frac{\partial^2 T(t)}{\partial t^2}\frac{\Delta t^2}{2!}-\frac{\partial^3 T(t)}{\partial t^3}\frac{\Delta t^3}{3!}+... \end{aligned} T(t+Δt)=T(t)+∂t∂T(t)Δt+∂t2∂2T(t)2!Δt2+∂t3∂3T(t)3!Δt3+...T(t−Δt)=T(t)−∂t∂T(t)Δt+∂t2∂2T(t)2!Δt2−∂t3∂3T(t)3!Δt3+...
两式相减,得
∂ T ( t ) ∂ t = T ( t + Δ t ) − T ( t − Δ t ) 2 Δ t + O ( Δ t 2 ) \frac{\partial T(t)}{\partial t}=\frac{T(t+\Delta t)-T(t-\Delta t)}{2\Delta t}+O(\Delta t^2) ∂t∂T(t)=2ΔtT(t+Δt)−T(t−Δt)+O(Δt2)
注意,偏导的精度的阶数为 O ( Δ t 2 ) O(\Delta t^2) O(Δt2),因为二阶偏导被完全消掉了。
把上式中的 T T T替换成 ( ρ ϕ ) (\rho\phi) (ρϕ),并代入到 ∂ ( ρ C ϕ C ) ∂ t V C + L ( ϕ C t ) = 0 \frac{\partial (\rho_C \phi_C)}{\partial t}V_C+L(\phi_C^t)=0 ∂t∂(ρCϕC)VC+L(ϕCt)=0,离散方程变为
( ρ C ϕ C ) t + Δ t − ( ρ C ϕ C ) t − Δ t 2 Δ t V C + L ( ϕ C t ) = 0 \frac{(\rho_C \phi_C)^{t+\Delta t}-(\rho_C \phi_C)^{t-\Delta t}}{2\Delta t}V_C+L(\phi_C^t)=0 2Δt(ρCϕC)t+Δt−(ρCϕC)t−ΔtVC+L(ϕCt)=0
接下来,引入空间离散项的代数方程,并根据之前设置的上标,瞬态标量方程的完整代数形式为
a C ∙ ϕ C = b C − ( a C ϕ C ∘ + ∑ F ∼ N B ( C ) a F ϕ F ∘ ) − a C ∘ ∘ ϕ C ∘ ∘ a_C^{\bullet} \phi_C = b_C-\left(a_C\phi_C^\circ+\sum_{F\sim NB(C)}a_F\phi_F^\circ\right) - a_C^{\circ\circ} \phi_C^{\circ\circ} aC∙ϕC=bC−⎝⎛aCϕC∘+F∼NB(C)∑aFϕF∘⎠⎞−aC∘∘ϕC∘∘
其中
a C ∙ = ρ C V C 2 Δ t a C ∘ ∘ = − ρ C ∘ ∘ V C 2 Δ t \begin{aligned} a_C^{\bullet} &= \frac{\rho_C V_C}{2\Delta t} \\ a_C^{\circ\circ} &= -\frac{\rho_C^{\circ\circ} V_C}{2\Delta t} \end{aligned} aC∙aC∘∘=2ΔtρCVC=−2ΔtρC∘∘VC
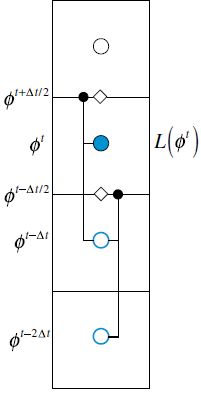
其架构如下图所示,显然,这个格式是显示算法,因为 ( ρ ϕ ) t + Δ t (\rho\phi)^{t+\Delta t} (ρϕ)t+Δt的获取只用到了旧时刻的值。然而现在需要存储两个旧时刻的值,但空间离散算子还是只需要其中一个旧时刻的值就好了。
对于CN格式的稳定性分析,可以把其最初的方程做些许修改来进行,使用如下近似:
ϕ ∘ ≈ ϕ + ϕ ∘ ∘ 2 \phi^\circ\approx\frac{\phi+\phi^{\circ\circ}}{2} ϕ∘≈2ϕ+ϕ∘∘
代数方程变为
a C ∙ ϕ C + 0.5 ( a C ϕ C + ∑ F ∼ N B ( C ) a F ϕ F ) = b C − 0.5 ( ( a C + 2 a C ∘ ∘ ) ϕ C ∘ ∘ + ∑ F ∼ N B ( C ) a F ϕ F ∘ ∘ ) a_C^{\bullet} \phi_C+0.5\left(a_C\phi_C+\sum_{F\sim NB(C)}a_F\phi_F\right) = b_C-0.5\left((a_C+2a_C^{\circ\circ})\phi_C^{\circ\circ}+\sum_{F\sim NB(C)}a_F\phi_F^{\circ\circ}\right) aC∙ϕC+0.5⎝⎛aCϕC+F∼NB(C)∑aFϕF⎠⎞=bC−0.5⎝⎛(aC+2aC∘∘)ϕC∘∘+F∼NB(C)∑aFϕF∘∘⎠⎞
如此一来,稳定性条件就变成了
a C + 2 a C ∘ ∘ ≤ 0 a_C+2a_C^{\circ\circ} \le 0 aC+2aC∘∘≤0
对于一维瞬态对流问题,有
Δ t ≤ 2 ρ C ∘ ∘ V C m ˙ e ∘ = 2 ρ C ∘ ∘ Δ x C Δ y C ρ C ∘ u C ∘ Δ y C ≈ 2 Δ x C ∣ v e ∘ ∣ \Delta t\le \frac{2\rho_C^{\circ\circ}V_C}{\dot m_e^\circ}=\frac{2\rho_C^{\circ\circ}\Delta x_C\Delta y_C}{\rho_C^\circ u_C^\circ \Delta y_C}\approx\frac{2\Delta x_C}{|\bold v_e^\circ|} Δt≤m˙e∘2ρC∘∘VC=ρC∘uC∘ΔyC2ρC∘∘ΔxCΔyC≈∣ve∘∣2ΔxC
其中对流项是用迎风格式离散的。使用前面定义的对流CFL数,上式变为
C F L c o n v ≤ 2 CFL^{conv} \le 2 CFLconv≤2
这个CFL数的最大限制可要比正向Eluer格式的大了,非常惬意,然而精度的提升则是更有意义,因为其让精确解的获取无需通过诉诸于更小的时间步长来实现,尤其是其把二阶导数都从误差中消掉了。随后章节中将展开更为详细的精确性分析。
2.5 实现细节
CN格式也可以通过把前向和后向Euler格式相加而推出,如下
Forward Euler → ( ρ C ϕ C ) t + Δ t − ( ρ C ϕ C ) t Δ t V C + L ( ϕ C t ) = 0 Backward Euler → ( ρ C ϕ C ) t − ( ρ C ϕ C ) t − Δ t Δ t V C + L ( ϕ C t ) = 0 \begin{aligned} & \text{Forward~Euler} \rightarrow \frac{(\rho_C \phi_C)^{t+\Delta t}-(\rho_C \phi_C)^t}{\Delta t}V_C+L(\phi_C^t)=0 \\ & \text{Backward~Euler} \rightarrow \frac{(\rho_C \phi_C)^{t}-(\rho_C \phi_C)^{t-\Delta t}}{\Delta t}V_C+L(\phi_C^t)=0 \end{aligned} Forward Euler→Δt(ρCϕC)t+Δt−(ρCϕC)tVC+L(ϕCt)=0Backward Euler→Δt(ρCϕC)t−(ρCϕC)t−ΔtVC+L(ϕCt)=0
两者相加
( ρ C ϕ C ) t + Δ t − ( ρ C ϕ C ) t Δ t V C + ( ρ C ϕ C ) t − ( ρ C ϕ C ) t − Δ t Δ t V C + 2 L ( ϕ C t ) = 0 → ( ρ C ϕ C ) t + Δ t − ( ρ C ϕ C ) t − Δ t 2 Δ t V C + L ( ϕ C t ) = 0 \begin{aligned} &\frac{(\rho_C \phi_C)^{t+\Delta t}-(\rho_C \phi_C)^t}{\Delta t}V_C+ \frac{(\rho_C \phi_C)^{t}-(\rho_C \phi_C)^{t-\Delta t}}{\Delta t}V_C+2L(\phi_C^t)=0 \\ \rightarrow &\frac{(\rho_C \phi_C)^{t+\Delta t}-(\rho_C \phi_C)^{t-\Delta t}}{2\Delta t}V_C+L(\phi_C^t)=0 \end{aligned} →Δt(ρCϕC)t+Δt−(ρCϕC)tVC+Δt(ρCϕC)t−(ρCϕC)t−ΔtVC+2L(ϕCt)=02Δt(ρCϕC)t+Δt−(ρCϕC)t−ΔtVC+L(ϕCt)=0
即Crank-Nicolson格式
该方程指明了CN格式的简单实现方法,即,在隐式框架下的两步法来实现。第一步是后向Euler格式,用于隐式找到 ( ρ ϕ ) t (\rho\phi)^t (ρϕ)t
( ρ C ϕ C ) t + Δ t V C L ( ϕ C t ) = ( ρ C ϕ C ) t − Δ t (\rho_C \phi_C)^{t}+\frac{\Delta t}{V_C}L(\phi_C^t)=(\rho_C \phi_C)^{t-\Delta t} (ρCϕC)t+VCΔtL(ϕCt)=(ρCϕC)t−Δt
然后在第2步中,显式算得 t + Δ t t+\Delta t t+Δt时刻的CN值
( ρ C ϕ C ) t + Δ t − ( ρ C ϕ C ) t Δ t V C = − L ( ϕ C t ) = ( ρ C ϕ C ) t − ( ρ C ϕ C ) t − Δ t Δ t V C ⇒ ( ρ C ϕ C ) t + Δ t = 2 ( ρ C ϕ C ) t − ( ρ C ϕ C ) t − Δ t \begin{aligned} & \frac{(\rho_C \phi_C)^{t+\Delta t}-(\rho_C \phi_C)^t}{\Delta t}V_C=-L(\phi_C^t)= \frac{(\rho_C \phi_C)^{t}-(\rho_C \phi_C)^{t-\Delta t}}{\Delta t}V_C \\ \Rightarrow & (\rho_C \phi_C)^{t+\Delta t}=2(\rho_C \phi_C)^{t}-(\rho_C \phi_C)^{t-\Delta t} \end{aligned} ⇒Δt(ρCϕC)t+Δt−(ρCϕC)tVC=−L(ϕCt)=Δt(ρCϕC)t−(ρCϕC)t−ΔtVC(ρCϕC)t+Δt=2(ρCϕC)t−(ρCϕC)t−Δt
在该推导过程中,假设瞬态时间步长 Δ t \Delta t Δt分为了两个等长的局部时间步长 Δ t l o c a l \Delta t_{local} Δtlocal,且 Δ t l o c a l \Delta t_{local} Δtlocal为设置时间步长 Δ t \Delta t Δt的一半。
值得注意的是,尽管CN格式是二阶精度,但是它仍旧是显式格式,且受限于CFL条件,如前所示。
2.6 Adams-Moulton格式
二阶Adams-Moulton格式的发展需要把 T T T在时刻 t − Δ t t-\Delta t t−Δt和 t − 2 Δ t t-2\Delta t t−2Δt的值使用Taylor级数展开成 t t t时刻的形式,即
T ( t − 2 Δ t ) = T ( t ) − ∂ T ( t ) ∂ t 2 Δ t + ∂ 2 T ( t ) ∂ t 2 4 Δ t 2 2 ! + . . . T ( t − Δ t ) = T ( t ) − ∂ T ( t ) ∂ t Δ t + ∂ 2 T ( t ) ∂ t 2 Δ t 2 2 ! + . . . \begin{aligned} T(t-2\Delta t)&=T(t)-\frac{\partial T(t)}{\partial t}2\Delta t+\frac{\partial^2 T(t)}{\partial t^2}\frac{4\Delta t^2}{2!}+... \\ T(t-\Delta t)&=T(t)-\frac{\partial T(t)}{\partial t}\Delta t+\frac{\partial^2 T(t)}{\partial t^2}\frac{\Delta t^2}{2!}+... \end{aligned} T(t−2Δt)T(t−Δt)=T(t)−∂t∂T(t)2Δt+∂t2∂2T(t)2!4Δt2+...=T(t)−∂t∂T(t)Δt+∂t2∂2T(t)2!Δt2+...
从上面两个式子出发,想办法把二阶偏导项消掉,得
∂ T ( t ) ∂ t = 3 T ( t ) − 4 T ( t − Δ t ) + T ( t − 2 Δ t ) 2 Δ t \frac{\partial T(t)}{\partial t}=\frac{3T(t)-4T(t-\Delta t)+T(t-2\Delta t)}{2\Delta t} ∂t∂T(t)=2Δt3T(t)−4T(t−Δt)+T(t−2Δt)
把上式中的 T T T替换成 ( ρ ϕ ) (\rho\phi) (ρϕ),并代入到 ∂ ( ρ C ϕ C ) ∂ t V C + L ( ϕ C t ) = 0 \frac{\partial (\rho_C \phi_C)}{\partial t}V_C+L(\phi_C^t)=0 ∂t∂(ρCϕC)VC+L(ϕCt)=0,离散方程变为
3 ( ρ C ϕ C ) t − 4 ( ρ C ϕ C ) t − Δ t + ( ρ C ϕ C ) t − 2 Δ t 2 Δ t V C + L ( ϕ C t ) = 0 \frac{3(\rho_C \phi_C)^t-4(\rho_C \phi_C)^{t-\Delta t}+(\rho_C \phi_C)^{t-2\Delta t}}{2\Delta t}V_C+L(\phi_C^t)=0 2Δt3(ρCϕC)t−4(ρCϕC)t−Δt+(ρCϕC)t−2ΔtVC+L(ϕCt)=0
接下来,引入空间离散项的代数方程,并根据之前设置的上标,瞬态标量方程的完整代数形式为
( a C ∙ + a C ) ϕ C + ∑ F ∼ N B ( C ) a F ϕ F = b C − a C ∘ ϕ C ∘ − a C ∘ ∘ ϕ C ∘ ∘ (a_C^{\bullet}+a_C) \phi_C +\sum_{F\sim NB(C)}a_F\phi_F = b_C-a_C^{\circ}\phi_C^\circ - a_C^{\circ\circ} \phi_C^{\circ\circ} (aC∙+aC)ϕC+F∼NB(C)∑aFϕF=bC−aC∘ϕC∘−aC∘∘ϕC∘∘
其中
a C ∙ = 3 ρ C V C 2 Δ t a C ∘ = − 2 ρ C ∘ V C Δ t a C ∘ ∘ = ρ C ∘ ∘ V C 2 Δ t \begin{aligned} a_C^{\bullet} &= \frac{3\rho_C V_C}{2\Delta t} \\ a_C^{\circ} &= -\frac{2\rho_C^{\circ} V_C}{\Delta t} \\ a_C^{\circ\circ} &= \frac{\rho_C^{\circ\circ} V_C}{2\Delta t} \end{aligned} aC∙aC∘aC∘∘=2Δt3ρCVC=−Δt2ρC∘VC=2ΔtρC∘∘VC
显然, a C ∘ ∘ a_C^{\circ\circ} aC∘∘系数是正值,所以 ϕ C ∘ ∘ \phi_C^{\circ\circ} ϕC∘∘的增加会导致 ϕ C \phi_C ϕC的减小。由于 a C ∘ a_C^\circ aC∘系数是负的,所以若 a C ∘ a_C^\circ aC∘较大,则可略微削减该不利影响。如此看来,尽管该格式是稳定的,然而其是无界的,在某些情况下会出现非物理振荡。
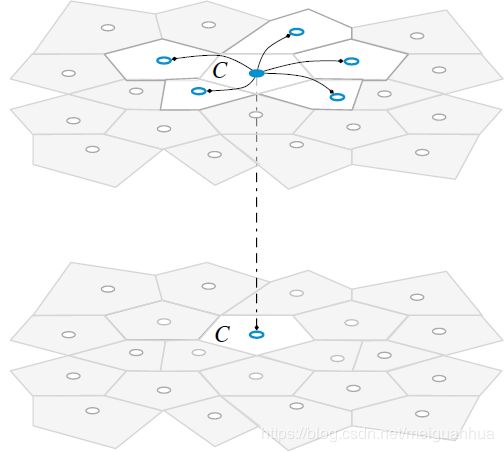
3 有限体积方法
有限体积方法对瞬态项的离散 和 对流项的离散 非常相似,只是积分是在时域单元而非空间单元上进行的,如下图所示。
对式 ∂ ( ρ C ϕ C ) ∂ t V C + L ( ϕ C t ) = 0 \frac{\partial (\rho_C \phi_C)}{\partial t}V_C+L(\phi_C^t)=0 ∂t∂(ρCϕC)VC+L(ϕCt)=0在时间区间 [ t − Δ t / 2 , t + Δ t / 2 ] [t-\Delta t/2, t+\Delta t/2] [t−Δt/2,t+Δt/2]做积分,即
∫ t − Δ t / 2 t + Δ t / 2 ∂ ( ρ C ϕ C ) ∂ t V C d t + ∫ t − Δ t / 2 t + Δ t / 2 L ( ϕ C t ) d t = 0 \int_{t-\Delta t/2}^{t+\Delta t/2}\frac{\partial (\rho_C \phi_C)}{\partial t}V_Cdt+\int_{t-\Delta t/2}^{t+\Delta t/2}L(\phi_C^t)dt=0 ∫t−Δt/2t+Δt/2∂t∂(ρCϕC)VCdt+∫t−Δt/2t+Δt/2L(ϕCt)dt=0
把 V C V_C VC作为常数处理,则第1项变为面通量差分形式,第2项用积分中值定理来做体积分,得
V C ( ρ C ϕ C ) t + Δ t / 2 − V C ( ρ C ϕ C ) t − Δ t / 2 + L ( ϕ C t ) Δ t = 0 V_C(\rho_C \phi_C)^{t+\Delta t/2}-V_C(\rho_C \phi_C)^{t-\Delta t/2}+L(\phi_C^t)\Delta t=0 VC(ρCϕC)t+Δt/2−VC(ρCϕC)t−Δt/2+L(ϕCt)Δt=0
该半离散瞬态方程可写成更加标准的形式,两边都除以 Δ t \Delta t Δt,得
( ρ C ϕ C ) t + Δ t / 2 − ( ρ C ϕ C ) t − Δ t / 2 Δ t V C + L ( ϕ C t ) = 0 \frac{(\rho_C \phi_C)^{t+\Delta t/2}-(\rho_C \phi_C)^{t-\Delta t/2}}{\Delta t}V_C+L(\phi_C^t)=0 Δt(ρCϕC)t+Δt/2−(ρCϕC)t−Δt/2VC+L(ϕCt)=0
为了得到完全离散方程,需要用插值廓线把在 t + Δ t / 2 t+\Delta t/2 t+Δt/2和 t − Δ t / 2 t-\Delta t/2 t−Δt/2处的面值用 t t t、 t − Δ t t-\Delta t t−Δt等处的单元值来表示。该廓线的选择可从对流项离散中汲取灵感。选择不同的廓线,毫无疑问会影响到方法的精确性和稳定性。基于此,需要说一下,空间算子的积分是时域二阶精度的,但是空间算子本身的精度(空间精度)则是由其离散时所采用的格式所决定的。
不管是使用的哪种廓线,通量都可用新值和旧值线性化为
F l u x T = F l u x C ϕ C + F l u x C ∘ ϕ C ∘ + F l u x V FluxT=FluxC\phi_C+FluxC^\circ\phi_C^\circ+FluxV FluxT=FluxCϕC+FluxC∘ϕC∘+FluxV
其中上标 ∘ ^\circ ∘仍旧代表旧值。完成该线性化处理后,代数方程的相关系数更替为下式,即可
a C ← a C + F l u x C b C ← b C − F l u x C ∘ ϕ C ∘ − F l u x V \begin{aligned} a_C & \leftarrow a_C+FluxC \\ b_C & \leftarrow b_C-FluxC^\circ\phi_C^\circ-FluxV \end{aligned} aCbC←aC+FluxC←bC−FluxC∘ϕC∘−FluxV
接下来展示某些廓线形式下的离散过程。
3.1 一阶瞬态格式
一阶隐式和显示Euler格式,可分别通过采用迎风和背风瞬态插值廓线来构造,如下。
3.2 一阶隐式Euler格式
使用一阶迎风插值廓线,即得到瞬态一阶隐式Euler格式。如上图所示,在时间单元面处的 ρ ϕ \rho\phi ρϕ值,等于迎风单元形心值,即
( ρ C ϕ C ) t + Δ t / 2 = ( ρ C ϕ C ) t ( ρ C ϕ C ) t − Δ t / 2 = ( ρ C ϕ C ) t − Δ t (\rho_C \phi_C)^{t+\Delta t/2}=(\rho_C \phi_C)^{t}\quad\quad (\rho_C \phi_C)^{t-\Delta t/2}=(\rho_C \phi_C)^{t-\Delta t} (ρCϕC)t+Δt/2=(ρCϕC)t(ρCϕC)t−Δt/2=(ρCϕC)t−Δt
那么半离散方程为
( ρ C ϕ C ) t − ( ρ C ϕ C ) t − Δ t Δ t V C + L ( ϕ C t ) = 0 \frac{(\rho_C \phi_C)^{t}-(\rho_C \phi_C)^{t-\Delta t}}{\Delta t}V_C+L(\phi_C^t)=0 Δt(ρCϕC)t−(ρCϕC)t−ΔtVC+L(ϕCt)=0
即一阶隐式Euler格式,线性化后的相关系数为
F l u x C = ρ C V C Δ t F l u x C ∘ = − ρ C ∘ V C Δ t F l u x V = 0 \begin{aligned} FluxC &= \frac{\rho_C V_C}{\Delta t} \\ FluxC^\circ &= -\frac{\rho_C^\circ V_C}{\Delta t} \\ FluxV &= 0 \end{aligned} FluxCFluxC∘FluxV=ΔtρCVC=−ΔtρC∘VC=0
3.2.1 数值扩散
由于这是一阶格式,那么,基于前面对流格式中获得的知识,该格式会产生数值扩散。可通过在时刻 t t t的Taylor级数展开,将其恢复到最初控制方程的形式,来确定数值扩散的值,即
( ρ ϕ ) t − Δ t = ( ρ ϕ ) t − ∂ ( ρ ϕ ) ∂ t ∣ t Δ t + ∂ 2 ( ρ ϕ ) ∂ t 2 ∣ t Δ t 2 2 + O ( Δ t 3 ) (\rho \phi)^{t-\Delta t}=(\rho \phi)^t-\left.\frac{\partial (\rho \phi)}{\partial t}\right|_t\Delta t +\left.\frac{\partial^2 (\rho \phi)}{\partial t^2}\right|_t\frac{\Delta t^2}{2}+O(\Delta t^3) (ρϕ)t−Δt=(ρϕ)t−∂t∂(ρϕ)∣∣∣∣tΔt+∂t2∂2(ρϕ)∣∣∣∣t2Δt2+O(Δt3)
调整为
( ρ ϕ ) t − ( ρ ϕ ) t − Δ t Δ t = ∂ ( ρ ϕ ) ∂ t ∣ t − ( Δ t 2 ) ∂ 2 ( ρ ϕ ) ∂ t 2 ∣ t − O ( Δ t 2 ) \frac{(\rho \phi)^{t}-(\rho \phi)^{t-\Delta t}}{\Delta t}= \left.\frac{\partial (\rho \phi)}{\partial t}\right|_t -\left(\frac{\Delta t}{2}\right)\left.\frac{\partial^2 (\rho \phi)}{\partial t^2}\right|_t-O(\Delta t^2) Δt(ρϕ)t−(ρϕ)t−Δt=∂t∂(ρϕ)∣∣∣∣t−(2Δt)∂t2∂2(ρϕ)∣∣∣∣t−O(Δt2)
把上式代入到离散格式中,得
∂ ( ρ ϕ ) ∂ t ∣ t + 1 V C L ( ϕ C t ) = ( Δ t 2 ) ∂ 2 ( ρ ϕ ) ∂ t 2 ∣ t ⏟ Numerical diffusion term + O ( Δ t 2 ) \left.\frac{\partial (\rho \phi)}{\partial t}\right|_t+\frac{1}{V_C}L(\phi_C^t)= \underbrace{\left(\frac{\Delta t}{2}\right)\left.\frac{\partial^2 (\rho \phi)}{\partial t^2}\right|_t}_\text{Numerical~diffusion~term}+O(\Delta t^2) ∂t∂(ρϕ)∣∣∣∣t+VC1L(ϕCt)=Numerical diffusion term (2Δt)∂t2∂2(ρϕ)∣∣∣∣t+O(Δt2)
实际上,给方程添加了个数值扩散项,且其与时间步长成正比,这跟对流格式中的迎风格式是相似的。所以呢,这个格式是无条件稳定的,其可对大时间步长产生稳定解。
3.3 一阶显示Euler格式
使用一阶背风插值廓线,即可得到瞬态一阶显示Euler格式,如上图所示,在时间单元面处的 ρ ϕ \rho\phi ρϕ值,等于背风单元形心值,即
( ρ C ϕ C ) t + Δ t / 2 = ( ρ C ϕ C ) t + Δ t ( ρ C ϕ C ) t − Δ t / 2 = ( ρ C ϕ C ) t (\rho_C \phi_C)^{t+\Delta t/2}=(\rho_C \phi_C)^{t+\Delta t}\quad\quad (\rho_C \phi_C)^{t-\Delta t/2}=(\rho_C \phi_C)^{t} (ρCϕC)t+Δt/2=(ρCϕC)t+Δt(ρCϕC)t−Δt/2=(ρCϕC)t
那么半离散方程为
( ρ C ϕ C ) t + Δ t − ( ρ C ϕ C ) t Δ t V C + L ( ϕ C t ) = 0 \frac{(\rho_C \phi_C)^{t+\Delta t}-(\rho_C \phi_C)^{t}}{\Delta t}V_C+L(\phi_C^t)=0 Δt(ρCϕC)t+Δt−(ρCϕC)tVC+L(ϕCt)=0
即一阶显式Euler格式,线性化后的相关系数为
F l u x C = ρ C V C Δ t F l u x C ∘ = − ρ C ∘ V C Δ t F l u x V = 0 \begin{aligned} FluxC &= \frac{\rho_C V_C}{\Delta t} \\ FluxC^\circ &= -\frac{\rho_C^\circ V_C}{\Delta t} \\ FluxV &= 0 \end{aligned} FluxCFluxC∘FluxV=ΔtρCVC=−ΔtρC∘VC=0
注意,现在新时刻是 t + Δ t t+\Delta t t+Δt,空间算子则是在旧时刻 t t t上衡量的,这样一来,右端项就完全已知了,可以直接用来得到 t + Δ t t+\Delta t t+Δt时刻的 ρ ϕ \rho\phi ρϕ,而不需要求解线性代数方程组。这是显式格式。
3.3.1 数值反扩散
基于 t t t时刻做Taylor展开
( ρ ϕ ) t + Δ t = ( ρ ϕ ) t + ∂ ( ρ ϕ ) ∂ t ∣ t Δ t + ∂ 2 ( ρ ϕ ) ∂ t 2 ∣ t Δ t 2 2 + O ( Δ t 3 ) (\rho \phi)^{t+\Delta t}=(\rho \phi)^t+\left.\frac{\partial (\rho \phi)}{\partial t}\right|_t\Delta t +\left.\frac{\partial^2 (\rho \phi)}{\partial t^2}\right|_t\frac{\Delta t^2}{2}+O(\Delta t^3) (ρϕ)t+Δt=(ρϕ)t+∂t∂(ρϕ)∣∣∣∣tΔt+∂t2∂2(ρϕ)∣∣∣∣t2Δt2+O(Δt3)
调整为
( ρ ϕ ) t + Δ t − ( ρ ϕ ) t Δ t = ∂ ( ρ ϕ ) ∂ t ∣ t + ( Δ t 2 ) ∂ 2 ( ρ ϕ ) ∂ t 2 ∣ t + O ( Δ t 2 ) \frac{(\rho \phi)^{t+\Delta t}-(\rho \phi)^{t}}{\Delta t}= \left.\frac{\partial (\rho \phi)}{\partial t}\right|_t +\left(\frac{\Delta t}{2}\right)\left.\frac{\partial^2 (\rho \phi)}{\partial t^2}\right|_t +O(\Delta t^2) Δt(ρϕ)t+Δt−(ρϕ)t=∂t∂(ρϕ)∣∣∣∣t+(2Δt)∂t2∂2(ρϕ)∣∣∣∣t+O(Δt2)
把上式代入到离散格式中,得
∂ ( ρ ϕ ) ∂ t ∣ t + 1 V C L ( ϕ C t ) = − ( Δ t 2 ) ∂ 2 ( ρ ϕ ) ∂ t 2 ∣ t ⏟ Numerical anti-diffusion term + O ( Δ t 2 ) \left.\frac{\partial (\rho \phi)}{\partial t}\right|_t+\frac{1}{V_C}L(\phi_C^t)= -\underbrace{\left(\frac{\Delta t}{2}\right)\left.\frac{\partial^2 (\rho \phi)}{\partial t^2}\right|_t}_\text{Numerical~anti-diffusion~term}+O(\Delta t^2) ∂t∂(ρϕ)∣∣∣∣t+VC1L(ϕCt)=−Numerical anti-diffusion term (2Δt)∂t2∂2(ρϕ)∣∣∣∣t+O(Δt2)
现在二阶差分项的符号是负的,类似于负扩散或反扩散,廓线上有压缩效应,这与对流格式中的背风格式非常像。反扩散项也是和时间步长呈正比关系的。当其与迎风对流格式联合起来,且Courant数为1的时候,对流项的数值扩散和 C F L c o n v = 1 CFL^{conv}=1 CFLconv=1的显式Euler格式的数值反扩散,两者幅值相等且符号相反,因此两者相互抵消,产生了近乎精确的解。尽管如此,确保 C F L c o n v = 1 CFL^{conv}=1 CFLconv=1是不切实际的,而且简单的一维网格也并非是实际问题的再现。
与反扩散效应相关的问题是数值不稳定性,其随着 Δ t \Delta t Δt的增加而增加,因此需要对时间步长施加较强的限制,可以通过负邻近系数准则来评估最大稳定时间步。
3.4 二阶瞬态Euler格式
与对流格式类似,二阶瞬态格式可通过线性插值廓线来构造。可选用对称廓线(中心差分)来产生Crank-Nicolson(CN)格式,也可选择迎风(二阶迎风格式)来产生Adams-Moulton格式,即,著名的隐式格式,二阶迎风Euler(Second Order Upwind Euler(SOUE))。
3.5 Crank-Nicolson(中心差分廓线)
采用在迎风和背风节点之间的线性插值来计算 ρ ϕ \rho\phi ρϕ值,便可获得上图所示的Crank-Nicolson格式。
对于均匀时间步,其数学表达式为
( ρ C ϕ C ) t + Δ t / 2 = 1 2 ( ρ C ϕ C ) t + Δ t + 1 2 ( ρ C ϕ C ) t ( ρ C ϕ C ) t − Δ t / 2 = 1 2 ( ρ C ϕ C ) t + 1 2 ( ρ C ϕ C ) t − Δ t \begin{aligned} & (\rho_C \phi_C)^{t+\Delta t/2}=\frac12(\rho_C \phi_C)^{t+\Delta t}+\frac12(\rho_C \phi_C)^{t} \\ & (\rho_C \phi_C)^{t-\Delta t/2}=\frac12(\rho_C \phi_C)^{t}+\frac12(\rho_C \phi_C)^{t-\Delta t} \end{aligned} (ρCϕC)t+Δt/2=21(ρCϕC)t+Δt+21(ρCϕC)t(ρCϕC)t−Δt/2=21(ρCϕC)t+21(ρCϕC)t−Δt
那么半离散方程为
( ρ C ϕ C ) t + Δ t − ( ρ C ϕ C ) t − Δ t 2 Δ t V C + L ( ϕ C t ) = 0 \frac{(\rho_C \phi_C)^{t+\Delta t}-(\rho_C \phi_C)^{t-\Delta t}}{2\Delta t}V_C+L(\phi_C^t)=0 2Δt(ρCϕC)t+Δt−(ρCϕC)t−ΔtVC+L(ϕCt)=0
即一阶显式Euler格式,线性化后的相关系数为
F l u x C = ρ C V C 2 Δ t F l u x C ∘ = 0 F l u x V = − ρ C ∘ ∘ V C 2 Δ t ϕ C ∘ ∘ \begin{aligned} FluxC &= \frac{\rho_C V_C}{2\Delta t} \\ FluxC^\circ &= 0 \\ FluxV &= -\frac{\rho_C^{\circ\circ} V_C}{2\Delta t}\phi_C^{\circ\circ} \end{aligned} FluxCFluxC∘FluxV=2ΔtρCVC=0=−2ΔtρC∘∘VCϕC∘∘
该格式是由 t t t和 t − Δ t t-\Delta t t−Δt时刻的值直接显式算得 t + Δ t t+\Delta t t+Δt时刻的值,所以是显式格式。其稳定性受CFL限制。
跟在有限差分框架中讲过的那样,上式可改写成两步走的样子,即,一阶隐式Euler步,和,插值形式的修正显式Euler步。
3.5.1 数值精度
基于 t t t时刻做Taylor展开
( ρ ϕ ) t + Δ t = ( ρ ϕ ) t + ∂ ( ρ ϕ ) ∂ t ∣ t Δ t + ∂ 2 ( ρ ϕ ) ∂ t 2 ∣ t Δ t 2 2 + ∂ 3 ( ρ ϕ ) ∂ t 3 ∣ t Δ t 3 6 + O ( Δ t 4 ) ( ρ ϕ ) t − Δ t = ( ρ ϕ ) t − ∂ ( ρ ϕ ) ∂ t ∣ t Δ t + ∂ 2 ( ρ ϕ ) ∂ t 2 ∣ t Δ t 2 2 − ∂ 3 ( ρ ϕ ) ∂ t 3 ∣ t Δ t 3 6 + O ( Δ t 4 ) (\rho \phi)^{t+\Delta t}=(\rho \phi)^t+\left.\frac{\partial (\rho \phi)}{\partial t}\right|_t\Delta t +\left.\frac{\partial^2 (\rho \phi)}{\partial t^2}\right|_t\frac{\Delta t^2}{2} +\left.\frac{\partial^3 (\rho \phi)}{\partial t^3}\right|_t\frac{\Delta t^3}{6} +O(\Delta t^4) \\ (\rho \phi)^{t-\Delta t}=(\rho \phi)^t-\left.\frac{\partial (\rho \phi)}{\partial t}\right|_t\Delta t +\left.\frac{\partial^2 (\rho \phi)}{\partial t^2}\right|_t\frac{\Delta t^2}{2} -\left.\frac{\partial^3 (\rho \phi)}{\partial t^3}\right|_t\frac{\Delta t^3}{6} +O(\Delta t^4) (ρϕ)t+Δt=(ρϕ)t+∂t∂(ρϕ)∣∣∣∣tΔt+∂t2∂2(ρϕ)∣∣∣∣t2Δt2+∂t3∂3(ρϕ)∣∣∣∣t6Δt3+O(Δt4)(ρϕ)t−Δt=(ρϕ)t−∂t∂(ρϕ)∣∣∣∣tΔt+∂t2∂2(ρϕ)∣∣∣∣t2Δt2−∂t3∂3(ρϕ)∣∣∣∣t6Δt3+O(Δt4)
两式相减,得
( ρ ϕ ) t + Δ t − ( ρ ϕ ) t − Δ t 2 Δ t = ∂ ( ρ ϕ ) ∂ t ∣ t + ∂ 3 ( ρ ϕ ) ∂ t 3 ∣ t Δ t 2 6 − O ( Δ t 3 ) \frac{(\rho \phi)^{t+\Delta t}-(\rho \phi)^{t-\Delta t}}{2\Delta t}= \left.\frac{\partial (\rho \phi)}{\partial t}\right|_t +\left.\frac{\partial^3 (\rho \phi)}{\partial t^3}\right|_t\frac{\Delta t^2}{6} -O(\Delta t^3) 2Δt(ρϕ)t+Δt−(ρϕ)t−Δt=∂t∂(ρϕ)∣∣∣∣t+∂t3∂3(ρϕ)∣∣∣∣t6Δt2−O(Δt3)
把上式代入到离散格式中,得
∂ ( ρ ϕ ) ∂ t ∣ t + 1 V C L ( ϕ C t ) = − ∂ 3 ( ρ ϕ ) ∂ t 3 ∣ t Δ t 2 6 + O ( Δ t 3 ) \left.\frac{\partial (\rho \phi)}{\partial t}\right|_t+\frac{1}{V_C}L(\phi_C^t)= -\left.\frac{\partial^3 (\rho \phi)}{\partial t^3}\right|_t\frac{\Delta t^2}{6} +O(\Delta t^3) ∂t∂(ρϕ)∣∣∣∣t+VC1L(ϕCt)=−∂t3∂3(ρϕ)∣∣∣∣t6Δt2+O(Δt3)
表明该格式具有二阶精度,第三项是色散项,会导致不稳定性。
3.6 二阶迎风Euler(SOUE)格式
使用上图所示的二阶迎风插值廓线,面 ρ ϕ \rho\phi ρϕ值的近似为
( ρ C ϕ C ) t + Δ t / 2 = 3 2 ( ρ C ϕ C ) t − 1 2 ( ρ C ϕ C ) t − Δ t ( ρ C ϕ C ) t − Δ t / 2 = 3 2 ( ρ C ϕ C ) t − Δ t − 1 2 ( ρ C ϕ C ) t − 2 Δ t \begin{aligned} & (\rho_C \phi_C)^{t+\Delta t/2}=\frac32(\rho_C \phi_C)^{t}-\frac12(\rho_C \phi_C)^{t-\Delta t} \\ & (\rho_C \phi_C)^{t-\Delta t/2}=\frac32(\rho_C \phi_C)^{t-\Delta t}-\frac12(\rho_C \phi_C)^{t-2\Delta t} \end{aligned} (ρCϕC)t+Δt/2=23(ρCϕC)t−21(ρ