分治算法总结

分治算法

动态规划与分治的区别是动态规划子问题有重叠而分治子问题相互独立

 

 分治算法的基本思想是将一个规模为N的问题分解为K个规模较小的子问题，这些子问题相互独立且与原问题性质相同。求出子问题的解，就可得到原问题的解。即一种分目标完成程序算法，简单问题可用二分法完成。（来自度娘）

一、概念

分而治之，将问题划分为更小的问题，直到最后子问题可以简单到直接求解，再将子问题合并为原问题得到原问题的解。例如，快排、归并等排序算法。

二、基本思路

大事化小，小事化了。将大问题化为子问题，分而治之。

例如，将一个规模为n的问题化为k个规模较小问题，这些问题相互独立且与原问题相似有相同的解觉问题的模式，递归解决这些问题，然后合并得到原问题的解。其中1

三、分治问题

1. 子问题缩小到一定规模可以简单解决。

2. 原问题可划分为有限个简单子问题。

3. 原问题可以用子问题的解求出。

4. 子问题之间相互独立。

四、分治步骤

1. 分解。将原问题分解成若干个与原问题形式相同的子问题。
2. 将子问题递归解决。
3. 将子问题合并为原问题。

五、相关题型

二分查找（折半查找）

二分查找应用在在一堆数中查找某个数，可以是数组，也可以是vector，应该也可以是set或者队列，二分查找的实现是分治思想典型体现，先将数组进行排序后，将数组对半分开为两个小区间，因为数是有序的（一般从小到大），所以对于每个子区间都有：右端点的数一定大于等于左端点的数，以分界点确定要查找的数应该在哪个区间，小于分界点就在做区间大于分界点就在右区间，然后再吧子区再次对半分为两个区间，直到分到每个区间只有一个数为止。

二分查找时间复杂度比较稳定O(logn),相比于顺序查找，二分查找要快的多，并且还要稳定。

代码如下：↓↓↓

#include
#include
#include
using namespace std;

int b_search(vector v,int num)
{
    int low = 0;
    int high = v.size()-1;
    while(low <= high)
    {
        int mid = (low+high)/2;
        if(num == v[mid])
            return 1;
        else if(num < v[mid])
            high = mid-1;
        else
            low = mid+1;
    }
    return 0;

}

int main()
{
    vector v;
    for(int i=0;i<10;i++)
    {
        v.push_back(i);
    }
    sort(v.begin(),v.end());
    cout<

快速排序

C++有现成的快排函数，但是快速排序的思想也是利用分治的思想。

1. 首先将第一个数与后面的数进行比较，将所有比他小的数放在它前面，此时以这个数为分界线，将两边划分为两个区间。

2. 对两边两个区间再次做相同的操作，直到将区间划分为每个区间只有一个数为止。

3. 排序完成。

盗来的图↑↑↑

代码如下：↓↓↓

void QuickSort(int array[], int start, int last)
{
    int i = start;
    int j = last;
    int temp = array[i];
    if (i < j)
    {
        while (i < j)
        {
            //
            while (i < j &&  array[j]>=temp )
                j--;
            if (i < j)
            {
                array[i] = array[j];
                i++;
            }

            while (i < j && temp > array[i])
                i++;
            if (i < j)
            {
                array[j] = array[i];
                j--;
            }
                        
        }
        //把基准数放到i位置
        array[i] = temp;
        //递归方法
        QuickSort(array, start, i - 1);
        QuickSort(array, i + 1, last);
    }
}

快速幂

利用分治思想把高次幂乘法时间复杂度降低

#include

using namespace std;

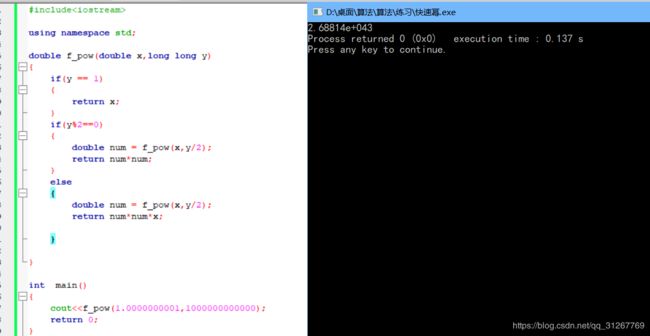
double f_pow(double x,long long y)
{
    if(y == 1)
    {
        return x;
    }
    if(y%2==0)
    {
        double num = f_pow(x,y/2);
        return num*num;
    }
    else
    {
        double num = f_pow(x,y/2);
        return num*num*x;

    }

}

int  main()
{
    cout<

即使求一万亿次方还是很快，惊呆脸。。。0.137秒

大整数乘法

模拟手工计算两个整数相乘的过程：逐位相乘，错位累加，最后进位。将数位对半分开，每一部分再次对半分开递归的操作下去，然后逐位相乘再相加。

string Add(string num1,string num2)
{
	reverse(num1.begin(),num1.end());
	reverse(num2.begin(),num2.end());
	string res;
	int len1=num1.length();
	int len2=num2.length();
	int len=min(len1,len2);
	int jw=0;
	for(int i=0;ilen2)
	{
		for(int i=len;i=num2
string Sub(string num1,string num2)
{
	reverse(num1.begin(),num1.end());
	reverse(num2.begin(),num2.end());
	int len1=num1.length();
	int len2=num2.length();
	int len=min(len1,len2);
	int jw=0;
	string res,result;
	for(int i=0;i=b)
		{
			res+=char(a-b+'0');
			jw=0;			
		}
		else
		{
			res+=char(a+10-b+'0');
			jw=1;
		}
	}
	for(int i=len;i=b)
		{
			res+=char(a-b+'0');
			jw=0;
		}
		else if(a=0;i--)
	{
		if(res[i]!='0'&&!flag)
		{
			result+=res[i];
			flag=true;
		}
		else if(flag)
			result+=res[i];
	}
	return result;
}

//两个n位大整数的乘法 
string Multiply1(string num1,string num2,int n)
{
	string a,b,c,d,ac,ad,bc,bd,adbc;
	a=num1.substr(0,n/2);
	b=num1.substr(n/2);
	c=num2.substr(0,n/2);
	d=num2.substr(n/2);
	ac=multiply(a,c);
	ad=multiply(a,d);
	bc=multiply(b,c);
	bd=multiply(b,d);
	adbc=Add(ad,bc);
	for(int i=0;i

如果采取以上算法的话时间复杂度可以降低到O(n^log2(3))。

---

还有以下类型问题，以后遇到了一一列举。

1. 线性时间选择

2. 最接近点对问题

3. 循环赛日程表

4. 棋盘覆盖

5. strassen矩阵乘法