算法设计与分析案例代码总结(三):回溯法
回溯法
简单概述
回溯法(深度优先搜索),其实是蛮力搜索法的一种升级版本,它把问题的解空间转换为了图或者树的结构表示,然后使用深度优先策略进行遍历,遍历的过程寻找所有的最优解或可行解。
回溯法按深度优先策略搜索问题的解空间树。首先从根节点出发搜索解空间树,当算法搜索至解空间树的某一节点时,先利用剪枝函数判断该节点是否可行(即能得到问题的解)。如果不可行,则跳过对该节点为根的子树的搜索,逐层向其祖先节点回溯;否则,进入该子树,继续按深度优先策略搜索。
回溯法的基本行为是搜索,搜索过程使用剪枝函数来为了避免无效的搜索。剪枝函数包括两类:1. 使用约束函数,剪去不满足约束条件的路径;2.使用限界函数,剪去不能得到最优解的路径。
问题的关键在于如何定义问题的解空间,转化成树(即解空间树)。解空间树分为两种:子集树和排列树。两种在算法结构和思路上大体相同。
回溯法的实现-递归和递推(迭代)
一、递归
思路简单,设计容易,但效率低,其设计范式如下:
对于初学递归的人,或者对递归不熟练的人而言可能不明白是怎么向上递归的,其实原因在于if与君,当判断为真时,就会去往backtrack(t+1),此时,循环体并没有执行完全,当最后一个t+1执行完毕后,就会往回跳转向上执行了。
//针对N叉树的递归回溯方法
void backtrack (int t)
{
if (t>n) output(x); //叶子节点,输出结果,x是可行解
else
for i = 1 to k//当前节点的所有子节点
{
x[t]=value(i); //每个子节点的值赋值给x
//满足约束条件和限界条件
if (constraint(t)&&bound(t))
backtrack(t+1); //递归下一层
}
}
二、递推(迭代)
算法设计相对复杂,但效率高。
//针对N叉树的迭代回溯方法
void iterativeBacktrack ()
{
int t=1;
while (t>0) {
if(ExistSubNode(t)) //当前节点的存在子节点
{
for i = 1 to k //遍历当前节点的所有子节点
{
x[t]=value(i);//每个子节点的值赋值给x
if (constraint(t)&&bound(t))//满足约束条件和限界条件
{
//solution表示在节点t处得到了一个解
if (solution(t)) output(x);//得到问题的一个可行解,输出
else t++;//没有得到解,继续向下搜索
}
}
}
else //不存在子节点,返回上一层
{
t--;
}
}
}
子集树和排列树
在一开始我们提到了子集数和排列树的概念,有些同学可能不明白什么是子集树什么是排列树,接下来我们做一个简单的介绍。
一、子集树
所给的问题是从n个元素的集合S中找出满足某种性质的子集时,相应的解空间成为子集树。
如0-1背包问题,从所给重量、价值不同的物品中挑选几个物品放入背包,使得在满足背包不超重的情况下,背包内物品价值最大。它的解空间就是一个典型的子集树。
回溯法搜索子集树的算法范式如下:
void backtrack (int t)
{
if (t>n) output(x);
else
for (int i=0;i<=1;i++) {
x[t]=i;
if (constraint(t)&&bound(t)) backtrack(t+1);
}
}
二、排列树
所给的问题是确定n个元素满足某种性质的排列时,相应的解空间就是排列树。
如旅行售货员问题,一个售货员把几个城市旅行一遍,要求走的路程最小。它的解就是几个城市的排列,解空间就是排列树。
回溯法搜索排列树的算法范式如下:
void backtrack (int t)
{
if (t>n) output(x);
else
for (int i=t;i<=n;i++) {
swap(x[t], x[i]);
if (constraint(t)&&bound(t)) backtrack(t+1);
swap(x[t], x[i]);
}
}
经典问题案例总结
N皇后问题
问题描述
N皇后问题是指在N*N的棋盘上放置N个皇后,使这N个皇后无法吃掉对方(也就是说两两不在一行,不在一列,也不在对角线上)。经典的是8皇后问题,这里我们为了简单,以4皇后为例。
首先利用回溯算法,先给第一个皇后安排位置,如下图所示,安排(1,1)然后给第二个皇后安排位置,可知(2,1),(2,2)都会产生冲突,因此可以安排在(2,3),然后安排第三个皇后,在第三行没有合适的位置,因此回溯到第二个皇后,重新安排第二个皇后的位置,安排到(2,4),然后安排第三个皇后到(3,2),安排第四个皇后有冲突,因此要回溯到第三个皇后,可知第三个皇后也就仅此一个位置,无处可改,故继续向上回溯到第二个皇后,也没有位置可更改,因此回溯到第一个皇后,更改第一个皇后的位置,继续上面的做法,直至找到所有皇后的位置,如下图所示。
这里为什么我们用4皇后做例子呢?因为3皇后是无解的。同时我们也可以看到回溯算法虽然也是Brute-Force,但是它可以避免去搜索很多的不可能的情况,因此算法是优于Brute-Force的。
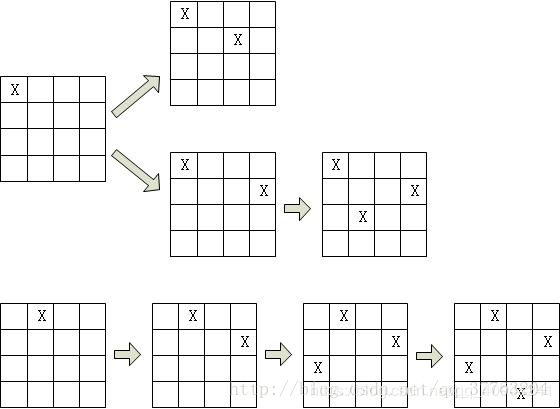
代码实现
package backTracking;
public class NQueens {
private int[] x;//当前解
private int N;//皇后个数
private int sum = 0;//当前已找到的可行方案数
private int totalNQueens(int n) {
N = n;
x = new int[N+1];
backTrace(1);
return sum;
}
/**
* col行这个点,x[col]列这个点,与已经存在的几个皇后,是否符合要求,放到这个位置上,
* @param col
* @return
*/
private boolean place(int col){
for(int i = 1; i < col; i++){
if(Math.abs(col - i)==Math.abs(x[col]-x[i])||x[col]==x[i]){//判断列是否相同,行的差的绝对值和列的差的绝对值是否相同(对角线)
return false;
}
}
return true;
}
private void backTrace(int t) {
if(t>N){
sum++;
}else {
//第t行,遍历所有的节点
for(int j = 1; j <= N; j++) {
x[t] = j ;
//如果第j个节点可以放下皇后
if(place(t)){
//接着放下一个
backTrace(t+1);
}
}
}
}
public static void main(String[] args) {
NQueens n = new NQueens();
System.out.println(n.totalNQueens(5));
}
}
TSP问题(货郎担问题)
问题描述
某售货员要到若干城市去推销商品,已知各城市间的路程耗费(代价),如何选定一条从驻地出发,经过每个城市一遍,最后回到驻地的路线,使得总路程耗费最小。
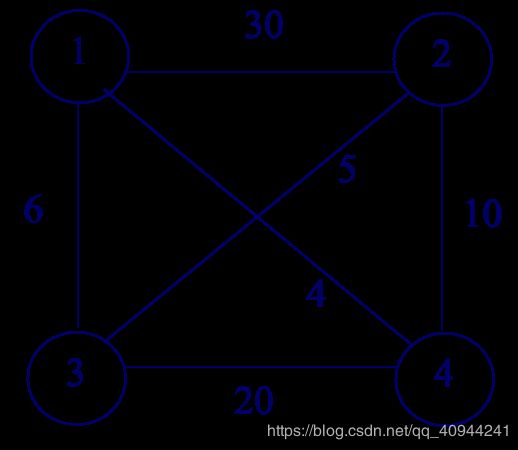
其实货郎担问题分为对称图和非对称图,对称图就如上图,即去往一个地方的花费,即路线,和回来的路线是相同的。而非对称的货郎担问题去往一个城市的花费和回来是不同的。非对称货郎担问题我们放在分支界限法中进行讨论。
解空间的表示
1)每个城市只出现有且仅有一次,设第i个出现的城市为xi ,则问题解向量:(x1, x2, … , xn)
2)显约束:xi = 1, 2, … , n
3)隐约束:
(1) 有从xi到xi+1的边;
(2)有从xn到x1的边;//能回到出发城市
(3)xi!=xk; //城市不能重复
求解过程
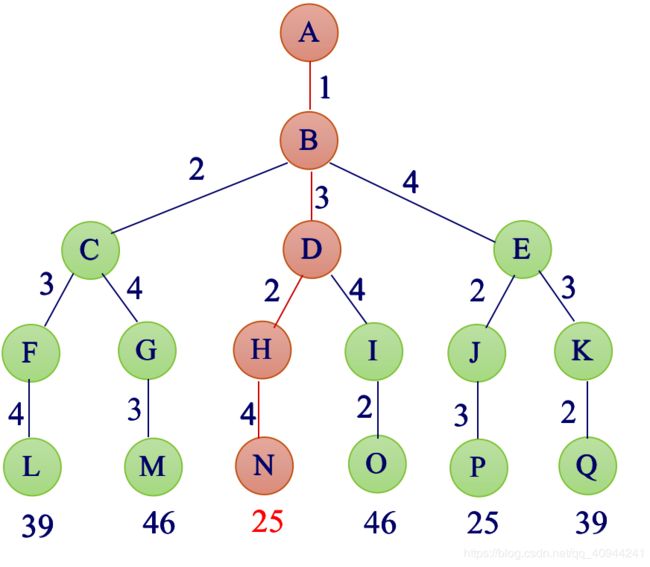
由上图可知,我们按照回溯法的思想,从开始的城市,即1开始,可以去往的城市有2,3,4,即产生三个子树,同理,2可以去往3,4(因为1已经走过),以此类推就可以得到上图的解空间树。
问题的关键在于剪枝函数的设计,从上图可以看出,回退到D点,去往I后的代价为26,但是我们在之前已经算出最小的代价为25了,而26明显大于26,这时候如果再加上一个城市一定会比25大,那么I后面的O就可以被剪去了,这么做就可以大大提高算法的效率。
代码实现
public class Back4TSP {
int NoEdge = -1;
int bigInt = Integer.MAX_VALUE;
int[][] a; // 邻接矩阵,存储任意两个城市间的代价
int cc = 0; // 存储当前代价
int bestc = bigInt;// 存储当前最小代价
int[] x; // 存储最优解
int[] bestx;// 存储当前最小代价对应的路线
int n = 0; // 城市数量
private void backtrack(int i) {//iΪ��ʼ���
if (i > n) {
//TODO
bestc = cc; bestx = x;
} else {
//TODO
for(int j = i;j <= n; j++) {
if(check(i,j)) {
swap(x[i],x[j]);
if(i < n && cc + a[x[i-1]][x[i]] < bestc) {
cc = cc + a[x[i-1]][x[i]]; //加入城市x[t]后更新cc
backtrack(i + 1);
cc = cc - a[x[i-1]][x[i]];
}
if(i == n && cc + a[x[i-1]][x[i]] + a[x[n]][x[1]] < bestc) {
cc = cc + a[x[i-1]][x[i]] + a[x[n]][x[1]];
backtrack(i + 1);
cc = cc - a[x[i-1]][x[i]] - a[x[n]][x[1]];
}
swap(x[i], x[j]); //恢复现场
}
}
}
}
private void swap(int i, int j) {
int temp = x[i];
x[i] = x[j];
x[j] = temp;
}
public boolean check(int i,int j) {
//TODO
if(i < 2) return true;
if(j < n && a[x[i-1]][x[j]] != NoEdge) return true;
if(j == n && (a[x[i-1]][x[j]] != NoEdge) && a[x[j]][x[1]] != NoEdge ) return true;
return false;
}
public void backtrack4TSP(int[][] b, int num) {
n = num;
x = new int[n + 1];
for (int i = 0; i <= n; i++)
x[i] = i;
bestx = new int[n + 1];
a = b;
backtrack(2);
}
}
测试类:
import org.junit.Assert;
import org.junit.Test;
public class Back4TSPTest {
@Test
public void testBacktrack4TSP() {
Back4TSP back4TSP = new Back4TSP();
int[][] b = { { -1, -1, -1, -1, -1 }, { -1, -1, 9, 19, 13 }, { -1, 21, -1, -1, 14 }, { -1, 1, 40, -1, 17 },
{ -1, 41, 80, 10, -1 } };
int n = 4;
back4TSP.backtrack4TSP(b, n);
Assert.assertTrue(back4TSP.bestc == 34);
}
}