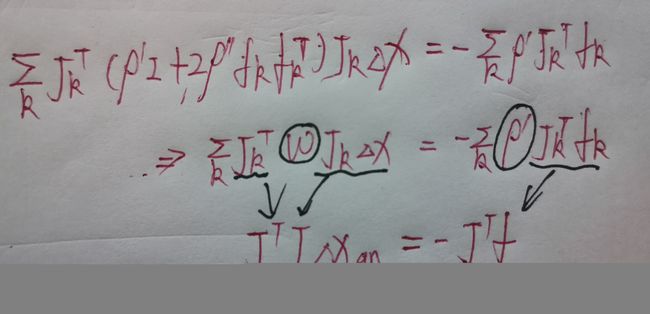VIO学习笔记(三)—— 基于优化的 IMU 与视觉信息融合
学习资料是深蓝学院的《从零开始手写VIO》课程,对课程做一些记录,方便自己以后查询,如有错误还请斧正。由于习惯性心算公式,所以为了加深理解,文章公式采用手写的形式。
VIO学习笔记(一)—— 概述
VIO学习笔记(二)—— IMU 传感器
基于优化的 IMU 与视觉信息融合
- 基于 Bundle Adjustment 的 VIO 融合
- 视觉 SLAM 里的 Bundle Adjustment 问题
- g2o or ceres 中采用如下的求解方式
- VIO 信息融合问题
- 预积分的简单理解
- 最小二乘问题的求解
- 最小二乘基础概念
- 定义
- 损失函数泰勒展开
- 损失函数泰勒展开性质
- 求解法
- 迭代法初衷
- 对损失函数泰勒展开
- 最速下降法(一阶梯度法): 适用于迭代的开始阶段
- 牛顿法(二阶梯度法):适用于最优值附近
- Damp Method
- 对残差函数泰勒展开
- 符号说明
- 基础
- Gauss-Newton Method
- Levenberg-Marquardt Method
- 阻尼因子的作用
- 阻尼因子初始值的选取
- 阻尼因子 μ 的更新策略
- Marquardt 策略
- Nielsen 策略 (被 g2o, ceres 采用)
- 鲁棒核函数的实现
- Triggs Correction
- Example: Cauchy Cost Function
- 核函数拓展
- 核函数控制参数的设定
- 回顾最小二乘求解
- VIO 残差函数的构建
- 视觉重投影误差
- 视觉重投影误差
- 逆深度参数化
- VIO 中基于逆深度的重投影误差
- IMU 测量值积分
- 测量值对世界坐标的积分
- IMU 预积分
- 预积分量
- 预积分误差
- 预积分的离散形式
- 预积分量的方差
- 疑问:
- Covariance Propagation(协方差传播)
- 一个有趣的例子
- 状态误差线性递推公式的推导
- 简介
- 基于泰勒展开的误差传递(应用于 EKF 的协方差预测)
- 基于误差随时间变化的递推方程
- 第一种方法不是很好么,为什么会想着去弄误差随时间的变化呢?
- 预积分的误差递推公式推导
- 残差 Jacobian 的推导
- 视觉重投影残差的 Jacobian
- IMU 误差相对于优化变量的 Jacobian
基于 Bundle Adjustment 的 VIO 融合
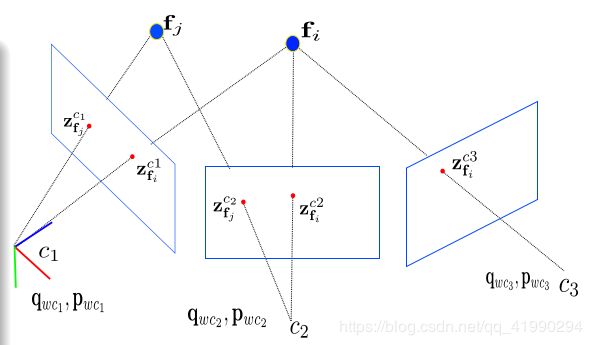
视觉 SLAM 里的 Bundle Adjustment 问题
已知:
状态量初始值:特征点的三维坐标,相机的位姿。
系统测量值:特征点在不同图像上的图像坐标。
解决方式:
构建误差函数,利用最小二乘得到状态量的最优估计:
arg min q , p , f ∑ i = 1 m ∑ j = 1 n ∣ ∣ π ( q w c i , p w c i , f j ) − z f j c i ∣ ∣ Σ i j \argmin_{q,p,f} \sum_{i=1}^m\sum_{j=1}^n ||π (q _{wc _i} , p _{wc _i} , f _j ) − z_{ f _j}^{c_i} ||_{Σ _{ij}} q,p,fargmini=1∑mj=1∑n∣∣π(qwci,pwci,fj)−zfjci∣∣Σij
符号定义:
q q q: 旋转四元数
p p p: 平移向量
f f f: 特征点3D坐标
c i c_i ci: 第i个相机系
π ( ⋅ ) π(·) π(⋅): 投影函数
Z f j c i Z_{f_j}^{c_i} Zfjci: c i c_i ci对 f j f_j fj的观测
∑ i j \sum_{ij} ∑ij: ∑ \sum ∑范数
g2o or ceres 中采用如下的求解方式
VIO 信息融合问题
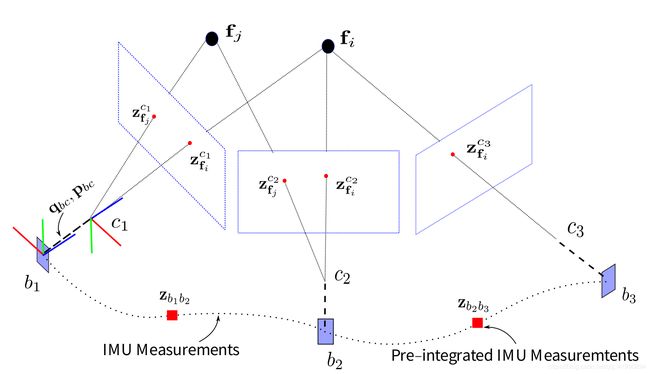
由于imu的数据采集频率大于相机的采集频率,所以在两个相机坐标系之间,存在多个imu坐标系即body坐标系,由于相机坐标系应根body坐标系相对应,所以对两图像间的imu数据进行预积分,使其变为一个。
预积分的简单理解
为什么要预积分,slam系统中为了减小优化求解器的负担,采用了关键帧策略,IMU的速率显然要快于关键帧的插入,它们之间的关系可以用下图很好的表示。
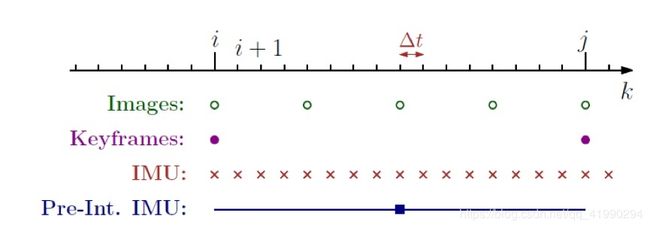
紧耦合的方式就是把imu和图像的信息共同来估计状态量,所以如何协调两者之间的关系了,预积分干了这么一件事,通过重新参数化,把关键帧之间的IMU测量值积分成相对运动的约束,避免了因为初始条件变化造成的重复积分。
用IMU的slam、vio算法有很多,有滤波器的比如MSCKF,有基于图优化的比如VINS,OKVIS,ORB-SLAM等。就拿ORB-SLAM来说吧, 在bundle adjustment里,参与对象是keyframe,比如有2个keyframe: K F 1 , K F 2 KF_1,KF_2 KF1,KF2, 他们的位姿分别为: P 1 w , P 2 w P_{1w},P_{2w} P1w,P2w,那么他们的相对位姿 :
P 21 = P 1 w ⋅ P 2 w − 1 P_{21}=P_{1w}·P_{2w}^{-1} P21=P1w⋅P2w−1
我们可以认为 P 21 P_{21} P21为估计项,是由SLAM的位姿直接算出来的。如果要构成一个优化问题,我们还需要知道误差项和测量项。没错,是IMU可以计算在这两个KF间的测量项 P i m u P_{imu} Pimu,预计分干的事情就是计算这个测量项。
r = P 21 ⋅ P i m u − 1 r=P_{21}·P_{imu}^{-1} r=P21⋅Pimu−1
在紧耦合的优化slam中,IMU就是提供了两个关键帧的相对测量,从而构建误差函数对关键帧姿态的迭代优化。当然实际应用中不会是这么简单的形式,这里面要对各个变量分别求取误差,然后求雅克比矩阵。
最小二乘问题的求解
最小二乘基础概念
定义
找到一个 n 维的变量 x ∗ ∈ R n x^*∈R^n x∗∈Rn ,使得损失函数 F (x) 取局部最小值:
F ( x ) = 1 2 ∑ i = 1 m ( f i ( x ) ) 2 F(x)=\frac{1}{2}\sum_{i=1}^m(f_i(x))^2 F(x)=21i=1∑m(fi(x))2
其中 f i f_i fi是残差函数,比如测量值和预测值之间的差,且有 m ≥ n。局部最小值指对任意 ∥ x − x ∗ ∥ < δ ∥x − x^∗ ∥ < δ ∥x−x∗∥<δ 有 F ( x ∗ ) ≤ F ( x ) F (x^∗ ) ≤ F (x) F(x∗)≤F(x)
损失函数泰勒展开
假设损失函数 F ( x ) F (x) F(x) 是可导并且平滑的,因此,二阶泰勒展开:
F ( x + ∆ x ) = F ( x ) + J ∆ x + 1 2 ∆ x ⊤ H ∆ x + O ( ∥ ∆ x ∥ 3 ) F (x + ∆x) = F (x) + J∆x + \frac12∆x ^⊤ H∆x + O (∥∆x∥ ^3) F(x+∆x)=F(x)+J∆x+21∆x⊤H∆x+O(∥∆x∥3)
其中 J 和 H 分别为损失函数 F 对变量 x 的一阶导和二阶导矩阵。
损失函数泰勒展开性质
忽略泰勒展开的高阶项,损失函数变成了二次函数,可以轻易得到如下性质:
如果在点 x s x_s xs 处有导数为 0 ,则称这个点为稳定点。
在点 x s x_s xs 处对应的 Hessian 为 H:
如果是正定矩阵,即它的特征值都大于 0,则在 x s x_s xs 处有 F ( x ) F (x) F(x) 为局部最小值;
如果是负定矩阵,即它的特征值都小于 0,则在 x s x_s xs 处有 F ( x ) F (x) F(x) 为局部最大值;
如果是不定矩阵,即它的特征值大于 0 也有小于 0 的,则 x s x_s xs 处为鞍点。
求解法
直接求解:线性最小二乘。
迭代下降法:适用于线性和非线性最小二乘。
迭代法初衷
找一个下降方向使损失函数随 x 的迭代逐渐减小,直到 x 收敛到 x ∗ x^∗ x∗ :
F ( x k + 1 ) < F ( x k ) F (x_{k+1} ) < F (x _k ) F(xk+1)<F(xk)
分两步:
第一,找下降方向单位向量 d,
第二,确定下降步长 α.
假设 α 足够小,我们可以对损失函数 F (x) 进行一阶泰勒展开:
F ( x + α d ) ≈ F ( x ) + α J d F (x + αd) ≈ F (x) + αJd F(x+αd)≈F(x)+αJd
只需寻找下降方向,满足:
J d < 0 Jd < 0 Jd<0
通过 line search 方法找到下降的步长: α ∗ = a r g m i n α > 0 F ( x + α d ) α ^∗ = argmin _{α>0} {F (x + αd)} α∗=argminα>0F(x+αd)
对损失函数泰勒展开
最速下降法(一阶梯度法): 适用于迭代的开始阶段
从下降方向的条件可知: J d = ∥ J ∥ c o s θ Jd = ∥J∥ cos θ Jd=∥J∥cosθ, θ θ θ 表示下降方向和梯度方向的夹角。当 θ = π θ = π θ=π ,有
d = − J T ∥ J ∥ d =\frac{-J^T}{∥J∥} d=∥J∥−JT
即梯度的负方向为最速下降方向。缺点:最优值附近震荡,收敛慢。
牛顿法(二阶梯度法):适用于最优值附近
在局部最优点 x ∗ x ^∗ x∗ 附近,如果 x + ∆ x x + ∆x x+∆x 是最优解,则损失函数对 ∆x的导数等于 0,对损失函数的二阶泰勒展式取一阶导有:
∂ ∂ ∆ x ( F ( x ) + J ∆ x + 1 2 ∆ x ⊤ H ∆ x ) = J ⊤ + H ∆ x = 0 \frac{∂}{∂∆x}(F (x) + J∆x + \frac12∆x ^⊤ H∆x )= J ^⊤ + H∆x = 0 ∂∆x∂(F(x)+J∆x+21∆x⊤H∆x)=J⊤+H∆x=0
得到: ∆ x = − H − 1 J ⊤ ∆x = −H^{ −1} J ^⊤ ∆x=−H−1J⊤ 。缺点:二阶导矩阵计算复杂。
Damp Method
将损失函数的二阶泰勒展开记作
F ( x + ∆ x ) ≈ L ( ∆ x ) ≡ F ( x ) + J ∆ x + ∆ x ⊤ H ∆ x F (x + ∆x) ≈ L(∆x) ≡ F (x) + J∆x + ∆x ^⊤ H∆x F(x+∆x)≈L(∆x)≡F(x)+J∆x+∆x⊤H∆x
求以下函数的最小化:
∆ x ≡ a r g min ∆ x ( L ( ∆ x ) + 1 2 μ ∆ x ⊤ ∆ x ) ∆x ≡ arg\min_{∆x} (L(∆x) + \frac12μ∆x^ ⊤ ∆x) ∆x≡arg∆xmin(L(∆x)+21μ∆x⊤∆x)
其中, μ ≥ 0 μ ≥ 0 μ≥0为阻尼因子, 1 2 μ ∆ x ⊤ ∆ x = 1 2 μ ∥ ∆ x ∥ 2 \frac12 μ∆x ^⊤ ∆x = \frac12 μ∥∆x∥^ 2 21μ∆x⊤∆x=21μ∥∆x∥2是惩罚项(不让步长过大)。
对新的损失函数求一阶导,并令其等于 0 有:
L ′ ( ∆ x ) + μ ∆ x = 0 ⇒ ( H + μ I ) ∆ x = − J ⊤ L ^′ (∆x) + μ∆x = 0\\ ⇒ (H + μI) ∆x = −J ^⊤ L′(∆x)+μ∆x=0⇒(H+μI)∆x=−J⊤
对残差函数泰勒展开
符号说明
为了公式约简,可将残差组合成向量的形式。
f ⃗ ( x ) = [ f 1 ( x ) f 2 ( x ) … f 1 ( x ) ] \vec{f } (x)= \begin{bmatrix} f_1(x) \\ f_2(x) \\ … \\f_1(x) \\ \end{bmatrix} f(x)=⎣⎢⎢⎡f1(x)f2(x)…f1(x)⎦⎥⎥⎤
则有: f ⊤ ( x ) f ( x ) = ∑ i = 1 m ( f i ( x ) ) 2 f ^⊤ (x)f (x) = \sum_{i=1}^m (f _i (x))^2 f⊤(x)f(x)=∑i=1m(fi(x))2
同理,如果记 J ⃗ i ( x ) = ∂ f i ( x ) ∂ x \vec{J}_ i (x) = \frac{∂f_i(x)}{∂x} Ji(x)=∂x∂fi(x) 则有:
∂ f ⃗ ( x ) ∂ x = J ⃗ = [ J ⃗ 1 ( x ) J ⃗ 2 ( x ) … J ⃗ i ( x ) ] \frac{∂\vec{f}(x)}{∂x}= \vec{J} =\begin{bmatrix} \vec{J}_ 1 (x) \\ \vec{J}_ 2(x) \\ … \\\vec{J}_ i (x) \\ \end{bmatrix} ∂x∂f(x)=J=⎣⎢⎢⎡J1(x)J2(x)…Ji(x)⎦⎥⎥⎤
基础
残差函数 f ⃗ ( x ) \vec{f} (x) f(x) 为非线性函数,对其一阶泰勒近似有:
f ( x + ∆ x ) ≈ l ( ∆ x ) ≡ f ( x ) + J ∆ x f (x + ∆x) ≈ l(∆x) ≡ f (x) + J∆x f(x+∆x)≈l(∆x)≡f(x)+J∆x
请特别注意,这里的 J 是残差函数 f 的雅克比矩阵。代入损失函数:
F ( x + ∆ x ) ≈ L ( ∆ x ) ≡ 1 2 l ( ∆ x ) ⊤ l ( ∆ x ) = 1 2 f ⊤ f + ∆ x ⊤ J ⊤ f + 1 2 ∆ x ⊤ J ⊤ J ∆ x = F ( x ) + ∆ x ⊤ J ⊤ f + 1 2 ∆ x ⊤ J ⊤ J ∆ x F (x + ∆x) ≈ L(∆x) ≡ \frac12l(∆x) ^⊤ l(∆x)\\ \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad= \frac12f ^⊤ f + ∆x ^⊤ J ^⊤ f + \frac12∆x ^⊤ J ^⊤ J∆x\\ \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad= F (x)+ ∆x ^⊤ J ^⊤ f + \frac12∆x ^⊤ J ^⊤ J∆x F(x+∆x)≈L(∆x)≡21l(∆x)⊤l(∆x)=21f⊤f+∆x⊤J⊤f+21∆x⊤J⊤J∆x=F(x)+∆x⊤J⊤f+21∆x⊤J⊤J∆x
这样损失函数就近似成了一个二次函数,并且如果雅克比是满秩的,则 J ⊤ J J ^⊤ J J⊤J 正定,损失函数有最小值。
另外, 易得: F ′ ( x ) = ( J ⊤ f ) ⊤ F ^′ (x) = (J ^⊤ f ) ^⊤ F′(x)=(J⊤f)⊤ ,以及 F ′ ′ ( x ) ≈ J ⊤ J F ^{′′} (x) ≈ J ^⊤ J F′′(x)≈J⊤J.
Gauss-Newton Method
令损失函数就近似式的一阶导等于 0,得到:
J ⊤ J ∆ x g n = − J ⊤ f J ^⊤ J ∆x_{ gn }= −J^ ⊤ f J⊤J∆xgn=−J⊤f
上式就是通常论文里看到的 H ∆ x g n = b H∆x _{gn} = b H∆xgn=b,称其为 normal equation.
Levenberg-Marquardt Method
Levenberg (1944) 和 Marquardt (1963) 先后对高斯牛顿法进行了改进,求解过程中引入了阻尼因子:
( J ⊤ J + μ I ) ∆ x l m = − J ⊤ f w i t h μ ≥ 0 (J^ ⊤ J + μI )∆x_{lm} = −J ^⊤ f \quad \quad \quad with \quad μ ≥ 0 (J⊤J+μI)∆xlm=−J⊤fwithμ≥0
阻尼因子的作用
μ > 0 μ > 0 μ>0 保证 ( J ⊤ J + μ I ) (J ^⊤ J + μI) (J⊤J+μI) 正定,迭代朝着下降方向进行。
μ μ μ 非常大,则 ∆ x l m = − 1 μ J ⊤ f = − 1 μ F ′ ( x ) ⊤ ∆x _{lm} = −\frac 1μ J ^⊤ f = − \frac1μ F^ ′ (x) ^⊤ ∆xlm=−μ1J⊤f=−μ1F′(x)⊤ , 接近最速下降法.
μ μ μ 比较小,则 ∆ x l m ≈ ∆ x g n ∆x _{lm} ≈ ∆x _{gn} ∆xlm≈∆xgn , 接近高斯牛顿法。
阻尼因子初始值的选取
阻尼因子 μ μ μ 大小是相对于 J ⊤ J J ^⊤ J J⊤J 的元素而言的。半正定的信息矩阵 J ⊤ J J^⊤ J J⊤J特征值 { λ j {λ_j } λj} 和对应的特征向量为 { v j {v _j } vj}。对 J ⊤ J J ^⊤ J J⊤J 做特征值分解分解后有: J ⊤ J = V Λ V ⊤ J ^⊤ J = VΛV ^⊤ J⊤J=VΛV⊤ 可得(不知道咋算出来的,先记住接着向下走吧,有时间再补特征分解的知识!!!):
∆ x l m = − ∑ j = 1 n v j T F ′ T λ j + μ v j ∆x_{ lm} = −\sum_{j=1}^n\frac{v_j^TF^{'T}}{λ_j+μ}v_j ∆xlm=−j=1∑nλj+μvjTF′Tvj
所以,一个简单的 μ 0 μ _0 μ0 初始值的策略就是:
μ 0 = τ ⋅ max ( J ⊤ J ) i i μ_ 0 = τ · \max{} (J ^⊤ J)_{ ii} μ0=τ⋅max(J⊤J)ii
通常,按需设定 τ ∼ [ 1 0 − 8 , 1 ] τ ∼ [10 ^{−8} , 1] τ∼[10−8,1]。
阻尼因子 μ 的更新策略
定性分析,直观感受阻尼因子的更新:
如果 ∆ x → F ( x ) ↑ ∆x → F (x) ↑ ∆x→F(x)↑ ,则 μ ↑ → ∆ x ↓ μ ↑→ ∆x ↓ μ↑→∆x↓, 增大阻尼减小步长,拒绝本次迭代。
如果 ∆ x → F ( x ) ↓ ∆x → F (x) ↓ ∆x→F(x)↓ ,则 μ ↓ → ∆ x ↑ μ ↓→ ∆x ↑ μ↓→∆x↑, 减小阻尼增大步长。加快收敛,减少迭代次数。- 定量分析,阻尼因子更新策略通过比例因子来确定的:
ρ = F ( x ) − F ( x + ∆ x l m ) L ( 0 ) − L ( ∆ x l m ) ρ =\frac{F (x) − F (x + ∆x _{lm} )}{L(0) − L (∆x _{lm} )} ρ=L(0)−L(∆xlm)F(x)−F(x+∆xlm)
其中: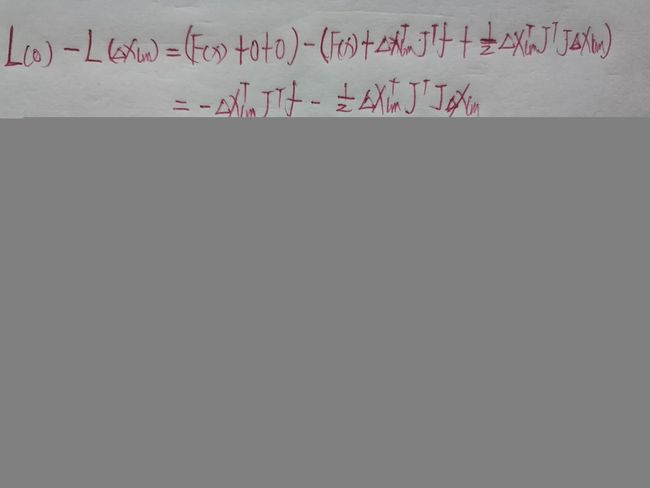
则有:
ρ = F ( x ) − F ( x + ∆ x l m ) 1 2 ∆ x l m T ( μ ∆ x l m + b ) b = − J T f ρ =\frac{F (x) − F (x + ∆x _{lm} )}{\frac12∆x_{lm}^T(μ∆x_{lm}+b)} \quad \quad \quad b=-J^Tf ρ=21∆xlmT(μ∆xlm+b)F(x)−F(x+∆xlm)b=−JTf
Marquardt 策略
首先比例因子分母始终大于 0,如果:
ρ < 0 ρ < 0 ρ<0, 则 F ( x ) ↑ F (x) ↑ F(x)↑ ,应该 μ ↑ → ∆ x ↓ μ ↑→ ∆x ↓ μ↑→∆x↓, 增大阻尼减小步长。
如果 ρ > 0 ρ > 0 ρ>0 且比较大,减小 μ μ μ, 让 LM 接近 Gauss-Newton 使得系统更快收敛。
反之,如果是比较小的正数,则增大阻尼 μ μ μ,缩小迭代步长。
1963 年 Marquardt 提出了一个如下的阻尼策略:
i f ρ < 0.25 μ : = μ ∗ 2 e l s e i f ρ > 0.75 μ : = μ / 3 if \quad \quad\quadρ < 0.25\\ \quad\quad\quad\quadμ := μ ∗ 2\\ elseif \quadρ > 0.75\\ \quad\quad\quad\quadμ := μ/3 ifρ<0.25μ:=μ∗2elseifρ>0.75μ:=μ/3
Marquardt 好不好呢?如下图所示 :
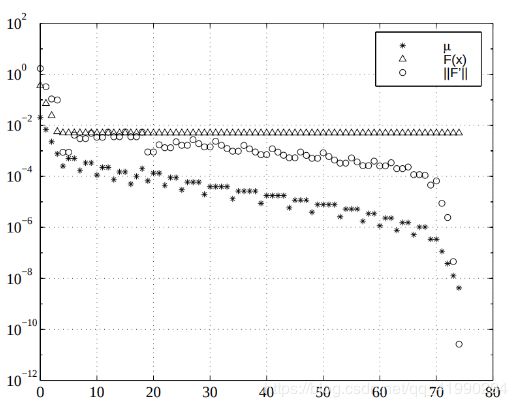
会看到 μ μ μ存在一定的跳动,这就导致步长存在一定的晃动,不稳定。
Nielsen 策略 (被 g2o, ceres 采用)
i f ρ > 0 μ : = μ ∗ m a x ( 1 3 , 1 − ( 2 ρ − 1 ) 3 ) ; ν : = 2 e l s e μ : = μ ∗ ν ; ν : = 2 ∗ ν \quad \quad if \quadρ > 0\\ \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quadμ := μ ∗ max(\frac13,1 − (2ρ − 1)^ 3 );ν := 2 \\ else\\ \quad\quad\quad\quad\quad\quad\quad\quad\quad\quadμ := μ ∗ ν;ν := 2 ∗ ν ifρ>0μ:=μ∗max(31,1−(2ρ−1)3);ν:=2elseμ:=μ∗ν;ν:=2∗ν
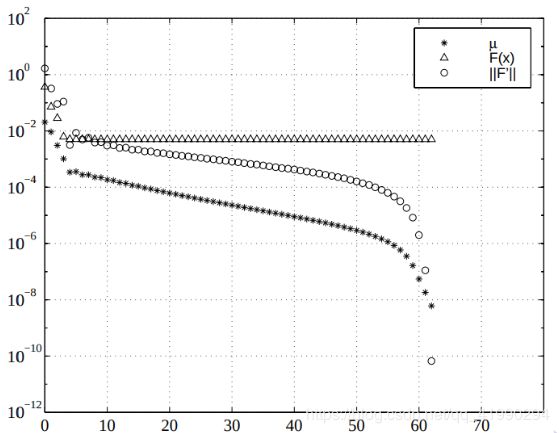
鲁棒核函数的实现
引言:最小二乘中遇到 outlier 怎么处理?核函数如何在代码中实现?有多种方法,这里主要介绍 g2o 和 ceres 中使用的 Triggs Correction .
Triggs Correction
鲁棒核函数直接作用残差 f k ( x ) f _k (x) fk(x) 上,最小二乘函数变成了如下形式:
min x 1 2 ∑ k ρ ( ∥ f k ( x ) ∥ 2 ) \min_x\frac12\sum_kρ (∥f _k (x)∥ ^2) xmin21k∑ρ(∥fk(x)∥2)
将误差的平方项记作 s k = ∥ f k ( x ) ∥ 2 s _k = ∥f _k (x)∥^ 2 sk=∥fk(x)∥2 , 则鲁棒核误差函数进行二阶泰勒展开有:
1 2 ρ ( s ) = 1 2 ( c o n s t + ρ ′ ∆ s + ρ ′ ′ ∆ 2 s ) \frac12ρ (s) = \frac12(const + ρ ^′ ∆s + ρ^ ′′ ∆^ 2 s) 21ρ(s)=21(const+ρ′∆s+ρ′′∆2s)
上述函数中 ∆ s k ∆s _k ∆sk 的计算稍微复杂一点:
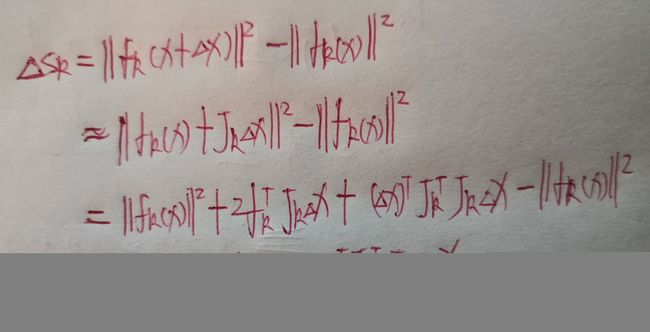
∆ s k ∆s _k ∆sk 代入 1 2 ρ ( s ) \frac12ρ (s) 21ρ(s)有:

代三角号的计算步骤很蒙,没有算出来,找了一下论文,发现论文也是这样写的:
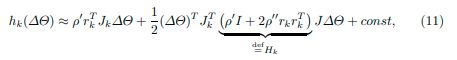
估计是哪个地方的知识点不到位把,再研究研究!!!
Example: Cauchy Cost Function
柯西鲁棒核函数的定义为:
ρ ( s ) = c 2 l o g ( 1 + s c 2 ) ρ(s) = c^ 2 log(1 +\frac{s}{c^2}) ρ(s)=c2log(1+c2s)
其中 c c c 为控制参数。对 s s s 的一阶导和二阶导为:
ρ ′ ( s ) = 1 1 + s c 2 , ρ ′ ′ ( s ) = − 1 c 2 ( ρ ′ ( s ) ) 2 ρ ^′ (s) =\frac{1}{1+\frac{s}{c^2}},\quad\quad\quad\quadρ ^{′ ′} (s) =-\frac{1}{c^2}(ρ ^′ (s) )^2 ρ′(s)=1+c2s1,ρ′′(s)=−c21(ρ′(s))2
核函数拓展
核函数控制参数的设定
95% efficiency rule (Huber, 1981):itprovides an asymptotic efficiency 95% that of linear regression for the normal distribution.
• 如果残差 f i f _i fi 是正态分布,Huber
c = 1.345 c = 1.345 c=1.345,
C a u c h y c = 2.3849 Cauchy c = 2.3849 Cauchyc=2.3849
• 如果残差非正态分布,需估计残差方差,然后对残差归一化。median absolute residual 方法
σ = 1.482 ⋅ m e d ( m e d ( r ) − r i ) σ = 1.482 · med(med(r) − r _i ) σ=1.482⋅med(med(r)−ri).
回顾最小二乘求解
- 找到一个合适的关于状态量 x 的残差函数 f i ( x ) f _i (x) fi(x),后续用 r, err等表示。
- 计算残差函数对状态量 x 的雅克比 J。
- 选定 cost function 以及其参数。
- LM 算法求解。
VIO 残差函数的构建
视觉重投影误差
视觉重投影误差
定义:
一个特征点在归一化相机坐标系下的估计值与观测值的差。
r c = [ x z − u y z − v ] r _c= \begin{bmatrix} \frac xz-u \\ \frac yz-v \\ \end{bmatrix} rc=[zx−uzy−v]
其中,待估计的状态量为特征点的三维空间坐标 ( x , y , z ) ⊤ (x, y, z) ^⊤ (x,y,z)⊤ ,观测值 ( u , v ) ⊤ (u, v) ^⊤ (u,v)⊤ 为特征在相机归一化平面的坐标。
逆深度参数化
特征点在归一化相机坐标系与在相机坐标系下的坐标关系为:
[ x y z ] = 1 λ [ u v 1 ] \begin{bmatrix} x \\y \\z\end{bmatrix}=\frac1λ\begin{bmatrix} u \\v \\1\end{bmatrix} ⎣⎡xyz⎦⎤=λ1⎣⎡uv1⎦⎤
其中 λ = 1 / z λ = 1/z λ=1/z 称为逆深度(更接近于高斯分布)。
VIO 中基于逆深度的重投影误差
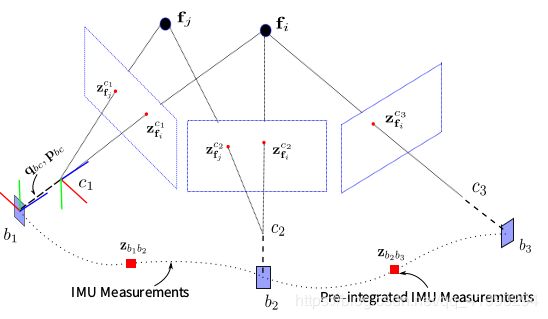
特征点逆深度在第 i 帧中初始化得到,在第 j 帧又被观测到,预测其在第 j 中的坐标为:
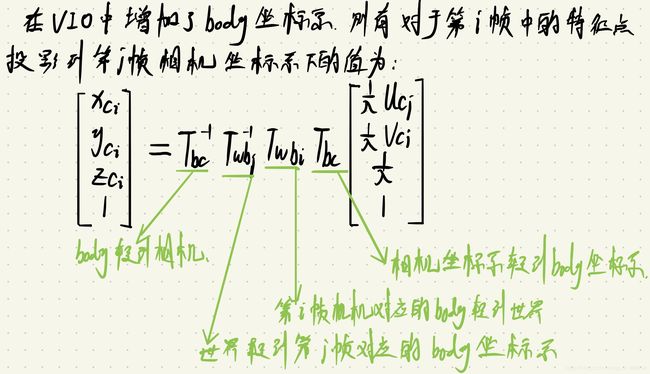
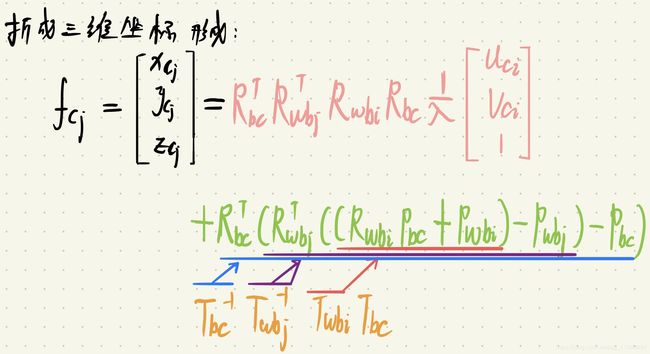
[ x c j y c j z c j 1 ] = T b c − 1 T w b j − 1 T w b i T b c [ 1 λ u c i 1 λ v c i 1 λ 1 ] \begin{bmatrix} x _{c_ j} \\y _{c_ j} \\z _{c_ j} \\1\end{bmatrix}=T^{−1}_{bc}T _{wb_j}^{-1}T_{wb_i} T_{bc} \begin{bmatrix} \frac1λu_{c_i} \\\frac1λv_{c_i} \\\frac1λ\\1\end{bmatrix} ⎣⎢⎢⎡xcjycjzcj1⎦⎥⎥⎤=Tbc−1Twbj−1TwbiTbc⎣⎢⎢⎡λ1uciλ1vciλ11⎦⎥⎥⎤
将i帧中观测到的数据变换到相机坐标系,将相机坐标系变换到body坐标系,将第i个body坐标系变换到世界坐标系,将世界坐标系变换到第j个body坐标系,将body坐标系变换到相机坐标系,得到第j帧的预测值。这期间相对于纯视觉多了相机坐标系变换到body坐标系,然后再由body坐标系变换回相机坐标系的过程。
视觉重投影误差为:
r c = [ x c i z c i − u c i y c i z c i − u c i ] r _c= \begin{bmatrix} \frac {x_{c_i}}{ z_{c_i}}-u_{c_i} \\ \frac {y_{c_i}}{ z_{c_i}}-u_{c_i} \\ \end{bmatrix} rc=[zcixci−ucizciyci−uci]
IMU 测量值积分
IMU 的真实值为 ω ω ω, a a a, 测量值为 ω ~ \tilde{ω} ω~, a ~ ã a~,则有:
ω ~ b = ω b + b g + n g a ~ = q b w ( a w + g w ) + b a + n a ω̃ ^b = ω^b + b^ g + n ^g\\ ã = q _{bw} (a ^w+g^w ) + b^a + n^a ω~b=ωb+bg+nga~=qbw(aw+gw)+ba+na
上标 g g g 表示 gyro, a a a 表示 acc, w w w 表示在世界坐标系 world, b b b 表示imu 机体坐标系 body。
PVQ 对时间的导数可写成:
p ˙ w b t = v t w v ˙ t w = a t w q ˙ w b t = q w b t ⊗ [ 0 1 2 w b t ] ṗ _{wb _t} = v _t^ w\\ v̇ _t^ w = a_ t^ w\\ q̇ _{wb _t} = q _{wb _t}⊗\begin{bmatrix} 0\\ \frac12w^{b_t}\\ \end{bmatrix} p˙wbt=vtwv˙tw=atwq˙wbt=qwbt⊗[021wbt]
测量值对世界坐标的积分
从第 i 时刻的 PVQ 对 IMU 的测量值进行积分得到第 j 时刻的 PVQ:
p w b j = p w b i + v i w ∆ t + ∬ t ∈ [ i , j ] ( q w b t a b t − g w ) δ t 2 v j w = v i w + ∫ t ∈ [ i , j ] ( q w b t a b t − g w ) δ t q w b j = ∫ t ∈ [ i , j ] q w b t ⊗ [ 0 1 2 w b t ] p_{wb_j} = p_{wb_i}+ v _i^ w ∆t +\iint_{t∈[i,j]}(q_{ wb _t} a ^{b t} − g ^w )δt^ 2\\ v _j ^w= v _i ^w+\int_{t∈[i,j]}(q_ {wb _t} a^{b_t} − g ^w )δt\\ q _{wb _j}=\int_{t∈[i,j]}q _{wb _t}⊗\begin{bmatrix} 0\\ \frac12w^{b_t}\\ \end{bmatrix} pwbj=pwbi+viw∆t+∬t∈[i,j](qwbtabt−gw)δt2vjw=viw+∫t∈[i,j](qwbtabt−gw)δtqwbj=∫t∈[i,j]qwbt⊗[021wbt]
每次 q wb t 优化更新后,都需要重新进行积分,运算量较大。所以引出下文预积分解决方案。
IMU 预积分
一个很简单的公式转换,就可以将积分模型转为预积分模型:
q w b t = q w b i ⊗ q b i b t q_{ wb _t} = q _{wb _i} ⊗ q _{b _i b _t} qwbt=qwbi⊗qbibt
那么,PVQ 积分公式中的积分项则变成相对于第 i 时刻的姿态,而不是相对于世界坐标系的姿态:
p w b j = p w b i + v i w ∆ t − 1 2 g w ∆ t 2 + q w b i ∬ t ∈ [ i , j ] ( q b i b t a b t ) δ t 2 v j w = v i w − g w ∆ t + q w b i ∫ t ∈ [ i , j ] ( q b i b t a b t ) δ t q w b j = q w b i ∫ t ∈ [ i , j ] q b i b t ⊗ [ 0 1 2 w b t ] p_{wb_j} = p_{wb_i}+ v _i^ w ∆t -\frac12g^w∆t ^2+q_{wb_i}\iint_{t∈[i,j]}(q _{b _i b _t} a ^{b t} )δt^ 2\\ v _j ^w= v _i ^w-g^w∆t+q_{wb_i}\int_{t∈[i,j]}(q _{b _i b _t} a ^{b t} )δt\\ q _{wb _j}=q_{wb_i}\int_{t∈[i,j]}q _{b _i b _t} ⊗\begin{bmatrix} 0\\ \frac12w^{b_t}\\ \end{bmatrix} pwbj=pwbi+viw∆t−21gw∆t2+qwbi∬t∈[i,j](qbibtabt)δt2vjw=viw−gw∆t+qwbi∫t∈[i,j](qbibtabt)δtqwbj=qwbi∫t∈[i,j]qbibt⊗[021wbt]
预积分量
预积分量仅仅跟 IMU 测量值有关,它将一段时间内的 IMU 数据直接积分起来就得到了预积分量:
α b i b j = ∬ t ∈ [ i , j ] ( q b i b t a b t ) δ t 2 β b i b j = ∫ t ∈ [ i , j ] ( q b i b t a b t ) δ t q b i b j = ∫ t ∈ [ i , j ] q b i b t ⊗ [ 0 1 2 w b t ] α _{b _i b _j} =\iint_{t∈[i,j]}(q _{b _i b _t} a ^{b t} )δt^ 2\\ β _{b _i b _j} = \int_{t∈[i,j]}(q _{b _i b _t} a ^{b t} )δt\\ q _{b _i b _j}=\int_{t∈[i,j]}q _{b _i b _t} ⊗\begin{bmatrix} 0\\ \frac12w^{b_t}\\ \end{bmatrix} αbibj=∬t∈[i,j](qbibtabt)δt2βbibj=∫t∈[i,j](qbibtabt)δtqbibj=∫t∈[i,j]qbibt⊗[021wbt]
重新整理下 PVQ 的积分公式,有:
[ p w b j v j w q w b j b j a b j g ] = [ p w b i + v i w ∆ t − 1 2 g w ∆ t 2 + q w b i α b i b j v i w − g w ∆ t + q w b i β b i b j q w b i q b i b j b i a b i g ] \begin{bmatrix} p_{wb_j} \\ v _j ^w \\ q _{wb _j} \\ b_j^a \\ b_j^g \end{bmatrix} = \begin{bmatrix} p_{wb_i}+ v _i^ w ∆t -\frac12g^w∆t ^2+q_{wb_i}α _{b _i b _j} \\ v _i ^w-g^w∆t+q_{wb_i}β _{b _i b _j} \\ q_{wb_i}q _{b _i b _j} \\ b_i^a \\ b_i^g \end{bmatrix} ⎣⎢⎢⎢⎢⎡pwbjvjwqwbjbjabjg⎦⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎡pwbi+viw∆t−21gw∆t2+qwbiαbibjviw−gw∆t+qwbiβbibjqwbiqbibjbiabig⎦⎥⎥⎥⎥⎤
预积分误差
定义:
一段时间内 IMU 构建的预积分量作为测量值,对两时刻之间的状态量进行约束,
[ r p r v r q r b a r b g ] 15 × 1 = [ q b i w ( p w b j − p w b i − v i w ∆ t + 1 2 g w ∆ t 2 ) − α b i b j q b i w ( v j w − v i w + g w ∆ t ) − β b i b j 2 [ q b j b i ⊗ ( q b i w ⊗ q w b j ) ] x y z b j a − b i a b j g − b i g ] \begin{bmatrix} r _p \\ r _v \\ r _q \\ r_{ba} \\ r_{bg} \end{bmatrix} _{15×1} = \begin{bmatrix} q_{b_iw}(p_{wb_j} -p_{wb_i}- v _i^ w ∆t + \frac12g^w∆t ^2)-α _{b _i b _j} \\ q_{b_iw}(v _j ^w - v _i ^w + g^w∆t) - β _{b _i b _j} \\ 2[q_{b _jb _i} ⊗ (q_{ b _i w} ⊗ q_{ wb _j} )] _{xyz} \\ b_j^a - b_i^a \\ b_j^g - b_i^g \end{bmatrix} ⎣⎢⎢⎢⎢⎡rprvrqrbarbg⎦⎥⎥⎥⎥⎤15×1=⎣⎢⎢⎢⎢⎡qbiw(pwbj−pwbi−viw∆t+21gw∆t2)−αbibjqbiw(vjw−viw+gw∆t)−βbibj2[qbjbi⊗(qbiw⊗qwbj)]xyzbja−biabjg−big⎦⎥⎥⎥⎥⎤
上面误差中位移,速度,偏置都是直接相减得到。第二项是关于四元数的旋转误差,其中 [·] xyz 表示只取四元数的虚部 (x, y, z) 组成的三维向量。
预积分的离散形式
这里使用 mid-point 方法,即两个相邻时刻 k 到 k+1 的位姿是用两个时刻的测量值 a, ω 的平均值来计算:
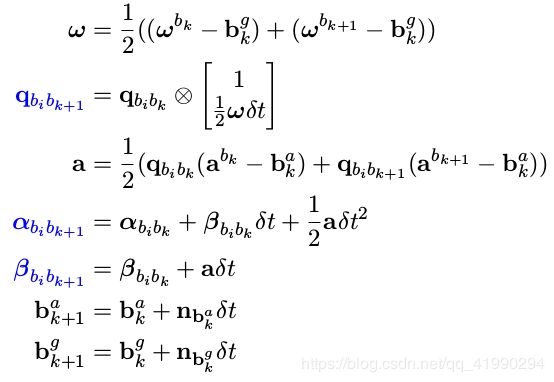
预积分量的方差
疑问:
一个 IMU 数据作为测量值的噪声方差我们能够标定。现在,一段时间内多个 IMU 数据积分形成的预积分量的方差呢?
Covariance Propagation(协方差传播)
已知一个变量 y = A x , x ∈ N ( 0 , Σ x ) y = Ax, x ∈ N (0, Σ _x ) y=Ax,x∈N(0,Σx), 则有 Σ y = A Σ x A ⊤ Σ _y = AΣ _x A ^⊤ Σy=AΣxA⊤
Σ y = E ( ( A x ) ( A x ) ⊤ ) = E ( A x x ⊤ A ⊤ ) = A Σ x A ⊤ Σ _y = E((Ax)(Ax)^ ⊤ )\\ = E(Axx ^⊤ A ^⊤ )\\ = AΣ x A ^⊤ Σy=E((Ax)(Ax)⊤)=E(Axx⊤A⊤)=AΣxA⊤
所以,要推导预积分量的协方差,我们需要知道imu 噪声和预积分量之间的线性递推关系。
假设已知了相邻时刻误差的线性传递方程:
η i k = F k − 1 η i k − 1 + G k − 1 n k − 1 η_{ ik} = F _{k−1} η _{ik−1} + G _{k−1} n _{k−1} ηik=Fk−1ηik−1+Gk−1nk−1
比如:状态量误差为 η i k = [ δ θ i k , δ v i k , δ p i k ] η_ {ik} = [δθ_{ ik} , δv _{ik} , δp _{ik} ] ηik=[δθik,δvik,δpik],测量噪声为 n k = [ n k g , n k a ] n _k = [n _k^ g , n _k^ a ] nk=[nkg,nka]。
误差的传递由两部分组成:当前时刻的误差传递给下一时刻,当前时刻测量噪声传递给下一时刻。
一个有趣的例子
综艺节目中常有传递信息的节目,前一个人根据上一个人的信息 + 自己的理解(测量)传递给下一个人,导致这个信息越传越错。
协方差矩阵可以通过递推计算得到:
Σ i k = F k − 1 Σ i k − 1 F k − 1 ⊤ + G k − 1 Σ n G k − 1 T Σ _{ik} = F _{k−1} Σ _{ik−1} F^ ⊤_{k−1} + G _{k−1} Σ _n G_{ k−1}^T Σik=Fk−1Σik−1Fk−1⊤+Gk−1ΣnGk−1T
其中, Σ n Σ _n Σn 是测量噪声的协方差矩阵,方差从 i 时刻开始进行递推, Σ i i = 0 Σ _{ii} = 0 Σii=0。
状态误差线性递推公式的推导
简介
通常对于状态量之间的递推关系是非线性的方程如 x k = f ( x k − 1 , u k − 1 ) x _k = f (x _{k−1} , u _{k−1}) xk=f(xk−1,uk−1),其中状态量为 x x x, u u u 为系统的输入量。
我们可以用两种方法来推导状态误差传递的线性递推关系:
一种是基于一阶泰勒展开的误差递推方程。
一种是基于误差随时间变化的递推方程。
基于泰勒展开的误差传递(应用于 EKF 的协方差预测)
令状态量为 x = x ^ + δ x x = x̂ + δx x=x^+δx,其中,真值为 x ^ x̂ x^,误差为 δ x δx δx。另外,输入量 u u u 的噪声为 n n n。
非线性系统 x k = f ( x k − 1 , u k − 1 ) x _k = f (x _{k−1} , u _{k−1} ) xk=f(xk−1,uk−1) 的状态误差的线性递推关系如下:
δ x k = F δ x k − 1 + G n k − 1 δx_ k = Fδx _{k−1} + Gn_{ k−1} δxk=Fδxk−1+Gnk−1
其中,F 是状态量 x k x _k xk 对状态量 x k − 1 x _{k−1} xk−1 的雅克比矩阵,G 是状态量 x k x_ k xk对输入量 u k − 1 u _{k−1} uk−1 的雅克比矩阵。
证明:对非线性状态方程进行一阶泰勒展开有:
x k = f ( x k − 1 , u k − 1 ) x ^ k + δ x k = f ( x ^ k − 1 + δ x k − 1 , u ^ k − 1 + n k − 1 ) x ^ k + δ x k = f ( x ^ k − 1 , u ^ k − 1 ) + F δ x k − 1 + G n k − 1 x _k = f (x _{k−1} , u _{k−1} )\\ x̂ _k + δx_ k = f (x̂_{ k−1} + δx_{ k−1} , û_{ k−1} + n _{k−1} )\\ x̂ _k + δx _k = f (x̂ _{k−1}, û _{k−1} ) + Fδx_{ k−1} + Gn _{k−1} xk=f(xk−1,uk−1)x^k+δxk=f(x^k−1+δxk−1,u^k−1+nk−1)x^k+δxk=f(x^k−1,u^k−1)+Fδxk−1+Gnk−1
基于误差随时间变化的递推方程
如果我们能够推导状态误差随时间变化的导数关系,比如:
δ x ′ = A δ x + B n δx^{'} =Aδx + Bn δx′=Aδx+Bn
则误差状态的传递方程为:
δ x k = δ x k − 1 + δ x k − 1 ′ ∆ t → δ x k = ( I + A ∆ t ) δ x k − 1 + B ∆ t n k − 1 δx _k = δx_{ k−1} + δx_{k−1} ^{'} ∆t\\ → δx _k = (I + A∆t)δx _{k−1}+ B∆tn_{k−1} δxk=δxk−1+δxk−1′∆t→δxk=(I+A∆t)δxk−1+B∆tnk−1
这两种推导方式的可以看出有:
F = I + A ∆ t , G = B ∆ t F = I + A∆t, G = B∆t F=I+A∆t,G=B∆t
第一种方法不是很好么,为什么会想着去弄误差随时间的变化呢?
这是因为 VIO 系统中已经知道了状态的导数和状态之间的转移矩阵。如:我们已经知道速度和状态量之间的关系:
v ˙ = R a b + g v̇ = Ra^ b + g v˙=Rab+g
那我们就可以推导速度的误差和状态误差之间的关系,再每一项上都加上各自的误差就有:
v ˙ + δ v ˙ = R ( I + [ δ θ ] × ) ( a b + δ a b ) + ( g + δ g ) δ v ˙ = R δ a b + R [ δ θ ] × ( a b + δ a b ) + δ g δ v ˙ = R δ a b − R [ a b ] × δ θ + δ g v̇ + δv̇= R (I + [δθ] _× )( a ^b + δa ^b) + (g + δg)\\ δv̇= Rδa^ b + R[δθ]_ × (a ^b + δa^ b) + δg\\ δv̇= Rδa^ b - R[a^b]_ × δθ + δg v˙+δv˙=R(I+[δθ]×)(ab+δab)+(g+δg)δv˙=Rδab+R[δθ]×(ab+δab)+δgδv˙=Rδab−R[ab]×δθ+δg
由此就能依次类推,轻易写出整个 A 和 B 其他方程了。
预积分的误差递推公式推导
首先回顾预积分的误差递推公式,将测量噪声也考虑进模型:
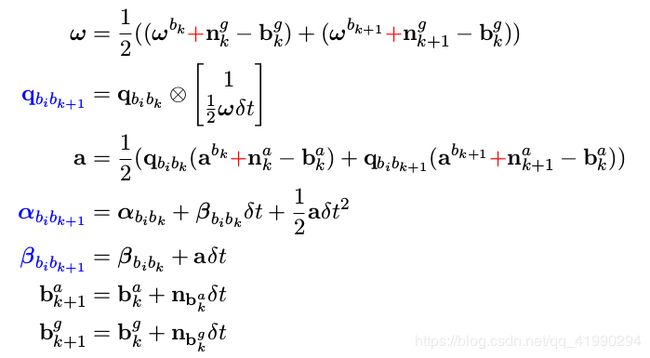
确定误差传递的状态量,噪声量,然后开始构建传递方程。
用前面一阶泰勒展开的推导方式 δ x k = F δ x k − 1 + G n k − 1 δx_ k = Fδx _{k−1} + Gn_{ k−1} δxk=Fδxk−1+Gnk−1,我们希望能推导出如下的形式:
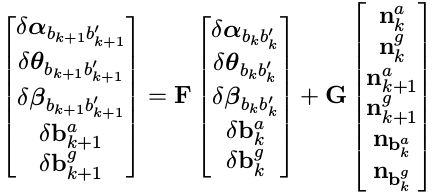
F, G 为两个时刻间的协方差传递矩阵。
这里我们直接给出 F, G 的最终形式,后面会对部分项进行详细推导:
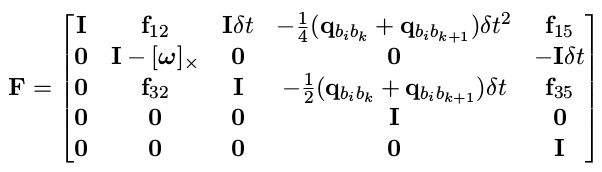
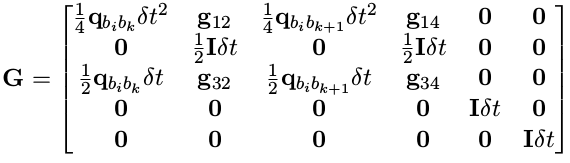
其中的系数为:
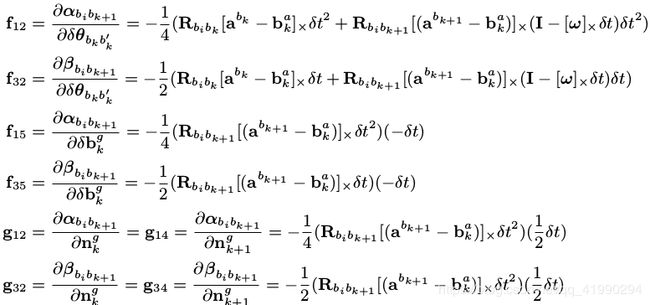
下面对F的第三行进行推导,其他行列的推导类似:


残差 Jacobian 的推导
视觉重投影残差的 Jacobian
视觉残差为:

对于第 i 帧中的特征点,它投影到第 j 帧相机坐标系下的值为:
拆成三维坐标形式为:
再推导各类 Jacobian 之前,为了简化公式,先定义如下变量:
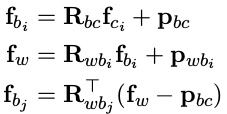
Jacobian 为视觉误差对两个时刻的状态量,外参,以及逆深度求导:
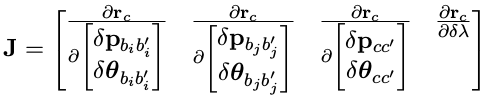
根据链式法则,Jacobian 的计算可以分两步走:
第一步误差对 f c j f _{c _j} fcj 求导:
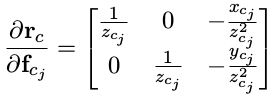
第二步 f c j 对各状态量求导:
- 对 i 时刻的状态量求导
a. 对 i 时刻位移求导,可直接写出如下:

b. 对 i 时刻角度增量求导
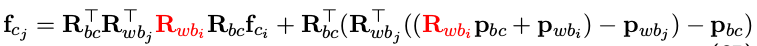
上面公式和 i 时刻角度相关的量并不多,下面为了简化,直接丢弃了不相关的部分
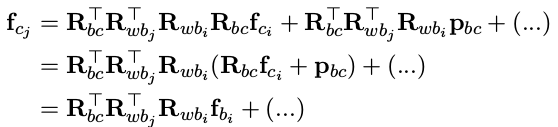
Jacobian 为

- 对 j 时刻的状态量求导
a. 对位移求导:
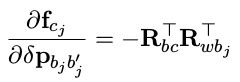
b. 对角度增量求导,同上面的操作,也简化一下公式
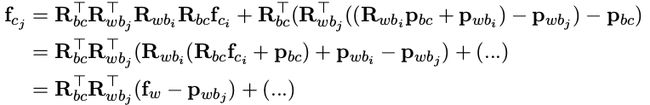
Jacobian 为
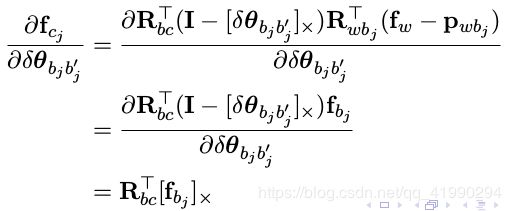
- 对 imu 和相机之间的外参求导
a. 对位移求导
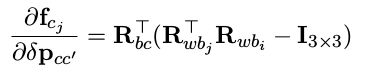
b. 对角度增量求导,由于 f c j 都和 R bc 有关,并且比较复杂,所以这次分两部分求导
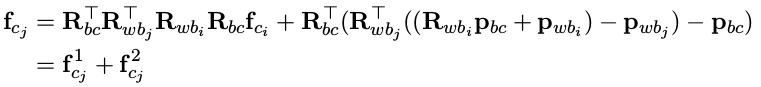
第一部分 Jacobian 为
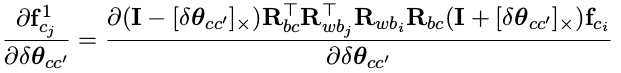
分子可写成:
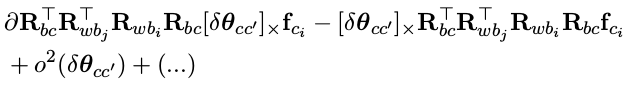
那么,第一部分的 Jacobian 为:
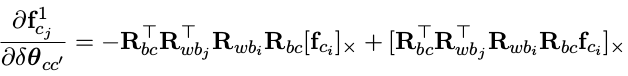
第二部分的 Jacobian 为:

两个 Jacobian 相加就是视觉误差对外参中的角度增量的最终结果。 - 视觉误差对特征逆深度的求导

IMU 误差相对于优化变量的 Jacobian
在求解非线性方程时,需要知道误差 e B 对两个关键帧 i, j 的状态量p, q, v, b a , b g 的 Jacobian。
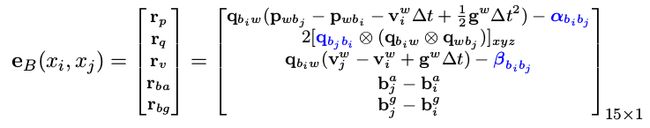
对 i, j 时刻的状态量 p, q, v 求导还是比较直观的,直接对误差公式进行计算就行。但是对 i 时刻的 b ai , b gi 求导就显得十分复杂,下面我们详细讨论。
因为 i 时刻的 bias 相关的预积分计算是通过迭代一步一步累计递推的,可以算但是太复杂。所以对于预积分量直接在 i 时刻的 bias 附近用一阶泰勒展开来近似,而不用真的去迭代计算。
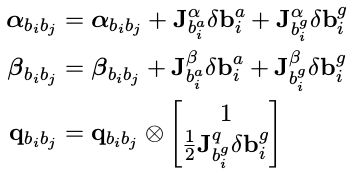
其中
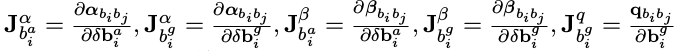
表示预积分量对 i 时刻的 bias 求导。
这些雅克比根据前面讨论的协方差传递公式,能一步步递推得到:
![]()
下面我们来讨论 IMU 误差相对于两帧的 PVQ 的 Jacobian:
由于 r p 和 r v 的误差形式很相近,对各状态量求导的 Jacobian 形式也很相似,所以这里只对 r v 的推导进行详细介绍。
- 对 i 时刻位移 Jacobian
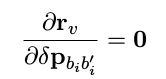
- 对 i 时刻旋转 Jacobian
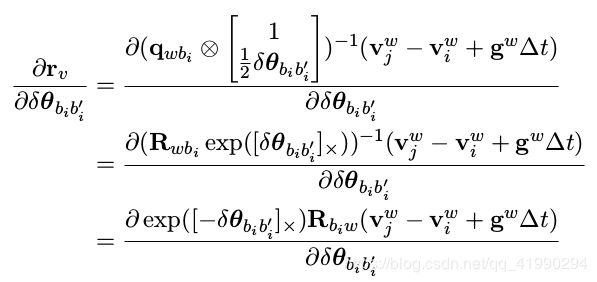
上式可写为:
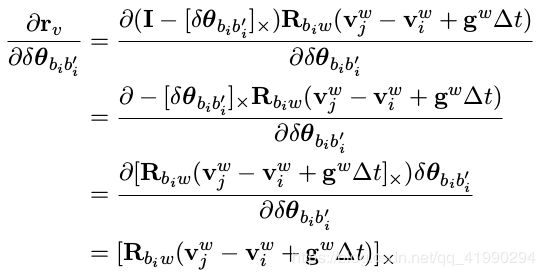
- 对 i 时刻速度 Jacobian:
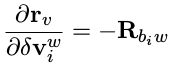
- 对 i 时刻的加速度 bias 的 Jacobian,注意 bias 量只和预积分 β 有关:
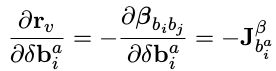
对rp的推导过程:
5. 对 i 时刻姿态求导
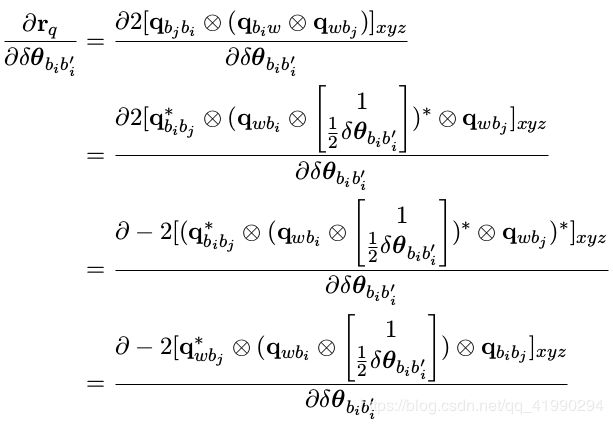
上式可化简为:
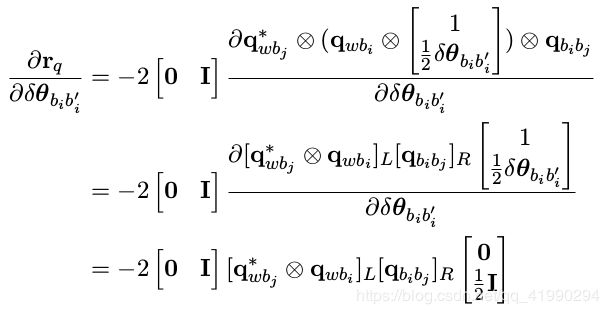
其中 [·] L 和 [·] R 为四元数转为左/右旋转矩阵的算子。
6. 角度误差对 j 时刻姿态求导
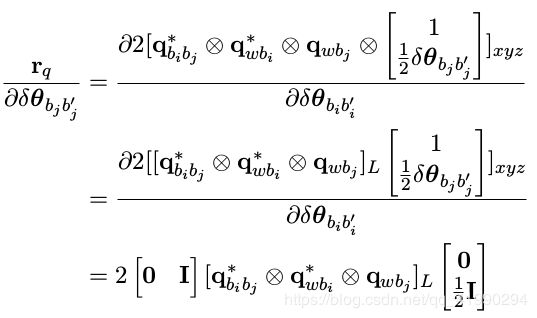
7. 角度误差对 i 时刻陀螺仪偏置 b gi
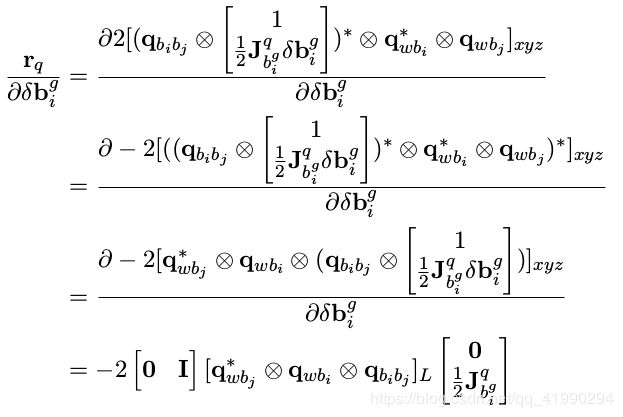
这公式……我傻了!!!
相关资料:
- Kaj Madsen, Hans Bruun Nielsen, and Ole Tingleff. “Methods for non-linear . least squares problems”. In: (1999).
- Christopher Zach. “Robust bundle adjustment revisited”. In: European Conference on Computer Vision. Springer. 2014, pp. 772–787.
- Bill Triggs et al. “Bundle adjustment—a modern synthesis”. In: International workshop on vision algorithms. Springer.1999, pp. 298–372.
- Kirk MacTavish and Timothy D Barfoot. “At all costs: A comparison of robust . cost functions for camera correspondence outliers”. In: 2015 12th Conference on Computer and Robot Vision. IEEE. 2015, . pp.62–69.