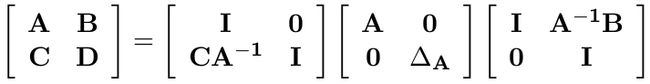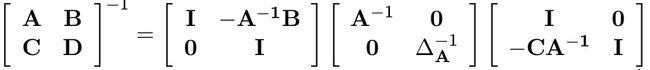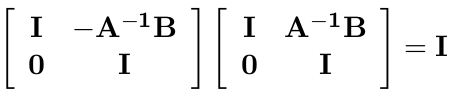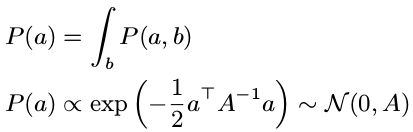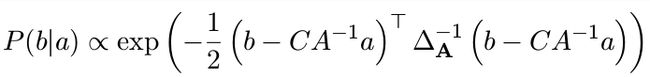VIO学习笔记(四)—— 基于滑动窗口算法的 VIO 系统:可观性和 一致性
学习资料是深蓝学院的《从零开始手写VIO》课程,对课程做一些记录,方便自己以后查询,如有错误还请斧正。由于习惯性心算公式,所以为了加深理解,文章公式采用手写的形式。
VIO学习笔记(一)—— 概述
VIO学习笔记(二)—— IMU 传感器
VIO学习笔记(三)—— 基于优化的 IMU 与视觉信息融合
基于滑动窗口算法的 VIO 系统:可观性和 一致性
- 本篇博客的主题
- 从高斯分布到信息矩阵
- SLAM 问题概率建模
- SLAM 问题求解
- 高斯分布和协方差矩阵
- 多元高斯分布
- toy example 1
- 样例对应的状态量协方差矩阵
- 对应的协方差矩阵的逆呢?
- toy example 1对应的信息矩阵
- 协方差元素 vs 信息矩阵元素
- toy example 2
- toy example 2 协方差矩阵的逆
- toy example 2 中的有趣现象
- toy example 1 中去除变量 x 3 x _3 x3
- 协方差如何变化?
- 信息矩阵如何变化?
- 舒尔补应用:边际概率, 条件概率
- 舒尔补的概念
- 舒尔补的来由
- 使用舒尔补分解的好处
- 舒尔补应用于多元高斯分布
- toy example
- 关于 P ( a ) P(a) P(a), P ( b ∣ a ) P(b|a) P(b∣a) 的协方差矩阵
- P(a) 的启示
- P(b|a) 的启示
- 关于 P(a), P(b|a) 的信息矩阵
- 为什么要讨论 P (a), P (b|a) 的信息矩阵?
- P(a), P(b|a) 的信息矩阵
- 回顾 toy example 1 中去除变量 x3 的操作
- 总结
- 滑动窗口算法
- toy example 3
- 最小二乘的图表示
- 最小二乘问题信息矩阵的构成
- 信息矩阵的稀疏性
- 信息矩阵组装过程的可视化
- 基于边际概率的滑动窗口算法
- 为什么 SLAM 需要滑动窗口算法?
- 滑动窗口算法大致流程
- 利用边际概率移除老的变量
- toy example 4
- 滑动窗口中的 FEJ 算法
- 系统回顾 toy example 3
- marg 发生后,留下的到底是什么信息?
- 新测量信息和旧测量信息构建新的系统
- 信息矩阵的零空间变化
- 滑动窗口算法导致的问题
- toy example
- 可观性的一种定义
- 滑动窗口中的问题
- 解决办法:First Estimated Jacobian
本篇博客的主题
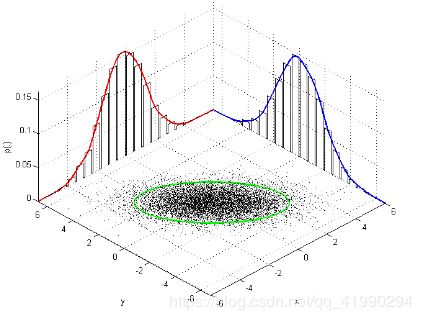
当维数变大时,求解计算量巨大。如何优雅的从多元高斯分布中丢弃变量?
p ( x , y ) → p ( x ) o r p ( y ) p(x, y) → p(x) \quad or \quad p(y) p(x,y)→p(x)orp(y)
从高斯分布到信息矩阵
SLAM 问题概率建模
考虑某个状态 ξ ξ ξ,以及一次与该变量相关的观测 r i r_ i ri。由于噪声的存在,观测服从概率分布 p ( r i ∣ ξ ) p (r _i |ξ) p(ri∣ξ)。
多次观测时,各个测量值相互独立,则多个测量 r = ( r 1 , . . . , r n ) ⊤ r = (r_ 1 , . . . , r _n ) ^⊤ r=(r1,...,rn)⊤ 构建的似然概率为:
p ( r ∣ ξ ) = ∏ i p ( r i ∣ ξ ) p(r|ξ) =∏_ip (r _i |ξ) p(r∣ξ)=i∏p(ri∣ξ)
如果知道机器人状态的先验信息 p(ξ),如 GPS, 车轮码盘信息等,则根据 Bayes 法则,有后验概率:
p ( ξ ∣ r ) = p ( r ∣ ξ ) p ( ξ ) p ( r ) p(ξ|r) =\frac{p(r|ξ)p(ξ)}{p(r)} p(ξ∣r)=p(r)p(r∣ξ)p(ξ)
通过最大后验估计,获得系统状态的最优估计:
ξ M A P = a r g max ξ p ( ξ ∣ r ) ξ _{MAP} = arg \max_ξ p(ξ|r) ξMAP=argξmaxp(ξ∣r)
SLAM 问题求解
后验公式中分母跟状态量无关,舍弃。最大后验变成了:
ξ M A P = a r g max ξ ∏ i p ( r i ∣ ξ ) p ( ξ ) ξ_{ MAP} = arg \max_ξ∏_ip (r _i |ξ) p(ξ) ξMAP=argξmaxi∏p(ri∣ξ)p(ξ)
即
ξ M A P = a r g min ξ [ − ∑ i log p ( r i ∣ ξ ) − log p ( ξ ) ] ξ_{ MAP} = arg \min_ξ[-∑_i\log p (r_ i |ξ) − \log p(ξ)] ξMAP=argξmin[−i∑logp(ri∣ξ)−logp(ξ)]
如果假设观测值服从多元高斯分布:
p ( r i ∣ ξ ) = N ( μ i , Σ i ) , p ( ξ ) = N ( μ ξ , Σ ξ ) p (r_ i |ξ) = N (μ_ i , Σ_ i ) , p (ξ) = N( μ _ξ , Σ_ ξ) p(ri∣ξ)=N(μi,Σi),p(ξ)=N(μξ,Σξ)
则有:
ξ M A P = a r g min ξ ∑ i ∥ r i − μ i ∥ Σ i 2 + ∣ ∣ ξ − μ ξ ∣ ∣ Σ ξ 2 ξ_{ MAP} = arg \min_ξ∑_i∥r _i − μ _i ∥^ 2_{ Σ _i} + ||ξ − μ_ ξ||^2_{Σ _ξ} ξMAP=argξmini∑∥ri−μi∥Σi2+∣∣ξ−μξ∣∣Σξ2
这个最小二乘的求解可以使用Gauss-Newton的解法:
J ⊤ Σ − 1 J δ ξ = − J ⊤ Σ − 1 r J ^⊤ Σ^{ −1} Jδξ = −J ^⊤ Σ^{ −1} r J⊤Σ−1Jδξ=−J⊤Σ−1r
高斯分布和协方差矩阵
多元高斯分布
零均值的多元高斯分布有如下概率形式:
p ( x ) = 1 Z e x p ( − 1 2 x ⊤ Σ − 1 x ) p(x) =\frac1Zexp (− \frac12x ^⊤ Σ^{ −1} x) p(x)=Z1exp(−21x⊤Σ−1x)
其中 Σ 是协方差矩阵,协方差矩阵的逆记作 Λ = Σ −1 .
比如变量 X 为三维的变量时,协方差矩阵为:
Σ = [ Σ 11 Σ 12 Σ 13 Σ 21 Σ 22 Σ 23 Σ 31 Σ 32 Σ 33 ] Σ= \begin{bmatrix} Σ _{11} & Σ _{12} & Σ _{13} \\ Σ _{21} & Σ _{22} & Σ _{23} \\ Σ _{31} & Σ _{32} & Σ _{33} \\ \end{bmatrix} Σ=⎣⎡Σ11Σ21Σ31Σ12Σ22Σ32Σ13Σ23Σ33⎦⎤
其中 Σ i j = E ( x i x j ) Σ_{ ij} = E(x_ i x_ j ) Σij=E(xixj) 为对应元素求期望。
toy example 1
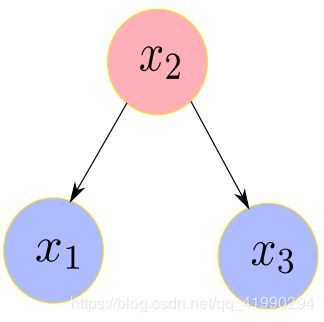
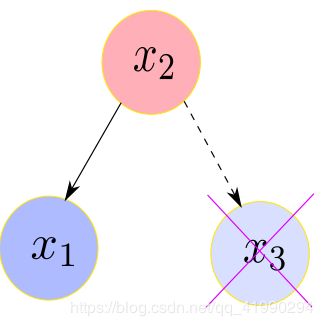
设 x 2 为室外的温度,x 1 , x 3 分别为房间 1和房间 3 的室内温度:
x 2 = v 2 x 1 = w 1 x 2 + v 1 x 3 = w 3 x 2 + v 3 x _2 = v_ 2\\ x _1 = w _1 x_ 2 + v_ 1\\ x _3 = w _3 x _2 + v_ 3 x2=v2x1=w1x2+v1x3=w3x2+v3
其中, v i v _i vi (从后面的公式来看,这个玩意很像( x − μ x-μ x−μ))相互独立,且各自服从协方差为 σ i 2 σ _i^ 2 σi2 的高斯分布。
样例对应的状态量协方差矩阵
从上述关系,根据协方差公式的计算方式,我们可以写出 x 的协方差矩阵,先从对角元素开始计算:
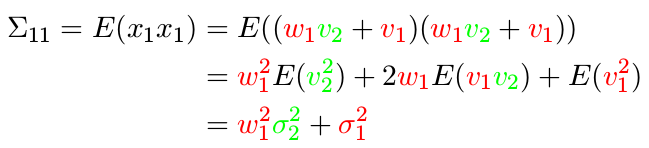
同理有
![]()
对于协方差矩阵的非对角元素:

以此类推,可以得到整个协方差矩阵:
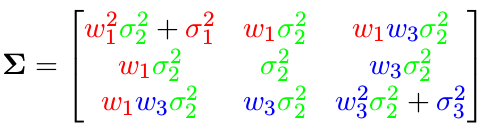
对应的协方差矩阵的逆呢?
通过计算联合高斯分布从而得到协方差矩阵的逆:
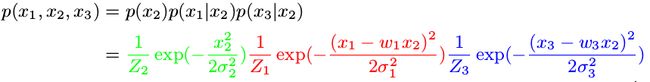
利用指数性质求出联合概率分布:

toy example 1对应的信息矩阵
由此得到协方差矩阵的逆,即信息矩阵:
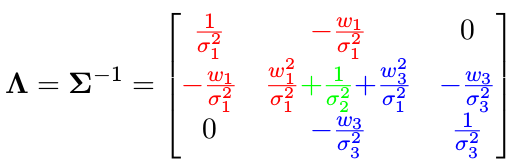
注意:信息矩阵中有两个元素为 0 ,它有什么具体含义呢?协方差逆矩阵中如果坐标为 (i, j) 的元素为 0,表示元素 i 和 j 关于其他变量条件独立,上面的例子中意味着变量 x 1 x _1 x1 和 x 3 x _3 x3 关于 x 2 x _2 x2 条件独立。
协方差元素 vs 信息矩阵元素
假设室内温度和室外温度正相关 ( w i > 0 ) (w _i > 0) (wi>0):
协方差中非对角元素 Σ i j > 0 Σ_{ ij} > 0 Σij>0 表示两变量是正相关。
信息矩阵中非对角元素为负数,甚至为 0。 Λ 12 < 0 Λ _{12} < 0 Λ12<0 表示在变量 x 3 x _3 x3 发生的条件下,元素 x 1 x_ 1 x1 和 x 2 x _2 x2 正相关。
toy example 2

比如特征三角化,两个相机 pose 得到特征三维坐标:
x 2 = w 1 x 1 + w 3 x 3 + v 2 x _2 = w _1 x _1 + w_ 3 x_ 3 + v_ 2 x2=w1x1+w3x3+v2
同理,根据协方差矩阵的定义,可以得到协方差矩阵:
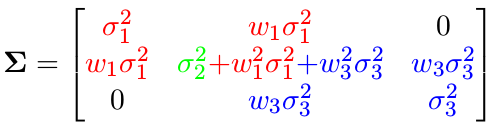
协方差矩阵中非对角元素为 0 表示变量之间没有相关性。这是否意味着信息矩阵中也会为 0 呢?
toy example 2 协方差矩阵的逆
按照例子 1 中的方式,求取协方差矩阵的逆:
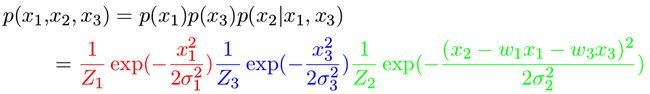
将变量整成向量形式:

toy example 2 中的有趣现象
从上面推导出的信息矩阵来看:
虽然 x 1 x _1 x1 和 x 3 x _3 x3不相关,但是不说明他们的信息矩阵对应元素 Λ 13 Λ _{13} Λ13为 0。
恰恰信息矩阵中 Λ 13 > 0 Λ _{13} > 0 Λ13>0, 表示的是在变量 x 2 x 2 x2 发生的条件下,变量 x 1 x _1 x1 , x 3 x_ 3 x3 成负相关。
对应上面的例子即 x 2 x _2 x2 为常数,如果 x 1 x _1 x1 大,则 x 3 x_ 3 x3 小。
疑问:如果我们移除变量,信息矩阵或协方差矩阵如何变化呢?
toy example 1 中去除变量 x 3 x _3 x3
协方差如何变化?
利用协方差的计算公式可知, x 1 x _1 x1 , x 2 x _2 x2 计算协方差时跟 x 3 x _3 x3 ,并无关系,所以
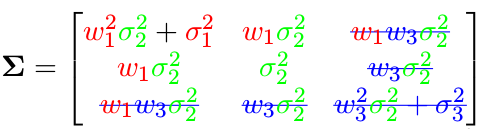
就能得到去除 x 3 x _3 x3 后的协方差矩阵:
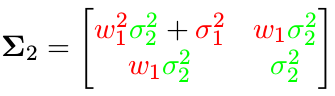
信息矩阵如何变化?
同样,我们只需要把信息矩阵公式中 x 3 x _3 x3 对应的部分 (蓝色) 去掉就可以:
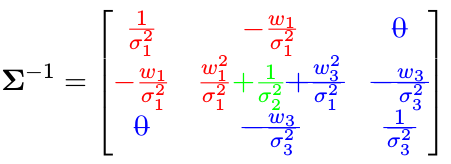
从而得到:
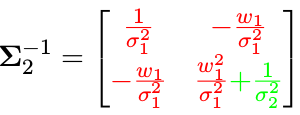
是不是非常简单?但是问题在于:实际操作过程中并不会有这种颜色标记。
这时,需要引入
marginalization (边缘化)和Schur’s complement (舒尔补)来解决这个问题.
舒尔补应用:边际概率, 条件概率
舒尔补的概念
给定任意的矩阵块 M,如下所示:
M = [ A B C D ] M= \begin{bmatrix} A & B\\ C & D \\ \end{bmatrix} M=[ACBD]
- 如果,矩阵块 D 是可逆的,则 A − B D − 1 C A − BD ^{−1 }C A−BD−1C 称之为 D 关于 M的
舒尔补。 - 如果,矩阵块 A 是可逆的,则 D − C A − 1 B D − CA^{ −1} B D−CA−1B 称之为 A 关于 M的舒尔补。
舒尔补的来由
将 M 矩阵变成上三角或者下三角形过程中,都会遇到舒尔补:
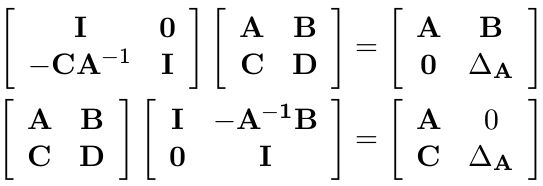
其中: ∆ A = D − C A − 1 B ∆ _A = D − CA^{ −1 }B ∆A=D−CA−1B。联合起来,将 M 变形成对角形:
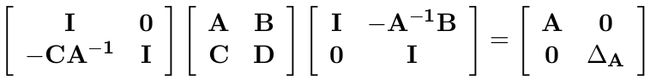
反过来,我们又能从对角形恢复成矩阵 M:
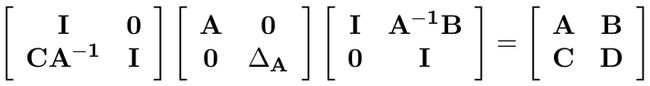
使用舒尔补分解的好处
快速求解矩阵 M 的逆:
舒尔补应用于多元高斯分布
toy example
假设多元变量 x 服从高斯分布,且由两部分组成: X = [ a b ] X= \begin{bmatrix} a\\ b \\ \end{bmatrix} X=[ab],变量之间构成的协方差矩阵为:
K = [ A C T C D ] K= \begin{bmatrix} A & C^T\\ C & D \\ \end{bmatrix} K=[ACCTD]
其中 A = c o v ( a , a ) A = cov(a, a) A=cov(a,a), D = c o v ( b , b ) D = cov(b, b) D=cov(b,b), C = c o v ( a , b ) C = cov(a, b) C=cov(a,b). 由此变量 x 的概率分布为:
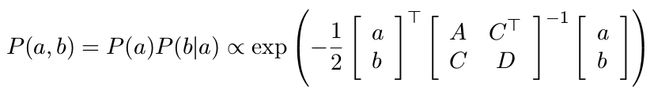
利用舒尔补一节公式, 对高斯分布进行分解,得:
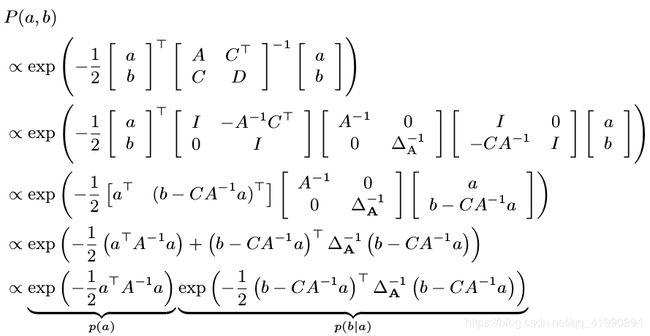
这意味着我们能从多元高斯分布 P ( a , b ) P(a,b) P(a,b) 中分解得到边际概率 p ( a ) p(a) p(a) 和条件概率 p ( b ∣ a ) p(b|a) p(b∣a)。
关于 P ( a ) P(a) P(a), P ( b ∣ a ) P(b|a) P(b∣a) 的协方差矩阵
P(a) 的启示
启示:
边际概率的协方差就是从联合分布中取对应的矩阵块就行了。
P(b|a) 的启示
启示: P ( b ∣ a ) ∼ N ( C A − 1 a , ∆ A ) P (b|a) ∼ N (CA^{ −1} a, ∆ _A ) P(b∣a)∼N(CA−1a,∆A)。
协方差变为 a 对应的舒尔补,均值也变了。
疑问三连:信息矩阵也是这样的吗? 如果不是,P(a) 的信息矩阵如何算? P(b|a) 的呢?
关于 P(a), P(b|a) 的信息矩阵
为什么要讨论 P (a), P (b|a) 的信息矩阵?
因为基于优化的 SLAM 问题中,我们往往直接操作的是信息矩阵,而不是协方差矩阵。所以,有必要知道边际概率,条件概率的信息矩阵是何形式。
P(a), P(b|a) 的信息矩阵
假设我们已知信息矩阵:

另外,由舒尔分解公式可知,协方差矩阵各块和信息矩阵之间有:
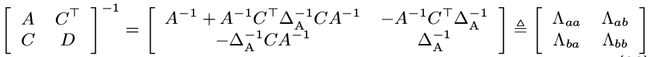
由条件概率 P (b|a) 的协方差为 ∆ A ∆ _A ∆A 以及上式,易得其信息矩阵为:
![]()
由边际概率 P (a) 的协方差为 A ,易得其信息矩阵为:
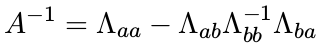
回顾 toy example 1 中去除变量 x3 的操作
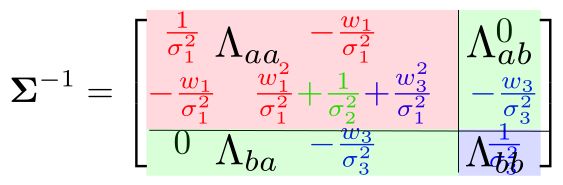
从联合分布 P ( x 1 , x 2 , x 3 ) P (x_ 1 , x _2 , x _3 ) P(x1,x2,x3) 中 marg 掉变量 x 3 x _3 x3 ,即 P ( x 1 , x 2 ) P (x _1 , x _2 ) P(x1,x2) 对应的信息矩阵可以用边际概率 P (a) 的协方差公式得到。

总结
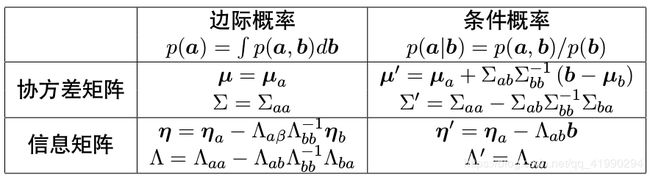
边际概率对于协方差矩阵的操作是很容易的,但不好操作信息矩阵。条件概率恰好相反,对于信息矩阵容易操作,不好操作协方差矩阵。表格总结如下 :
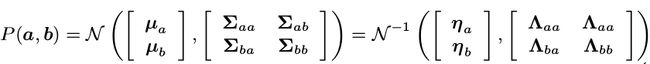
滑动窗口算法
toy example 3
最小二乘的图表示
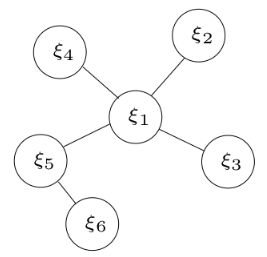
圆圈:表示顶点,需要优化估计的变量.
边:表示顶点之间构建的残差。有一元边(只连一个顶点),二元边,多元边…
有如下最小二乘系统,对应的图模型如有图所示:
ξ = a r g min ξ 1 2 ∑ i ∥ r i ∥ Σ i 2 ξ= arg \min_ξ\frac12∑_i∥r _i ∥^ 2_{ Σ _i} ξ=argξmin21i∑∥ri∥Σi2
其中
ξ = [ ξ 1 ξ 2 … ξ 6 ] , r = [ r 12 r 13 r 14 r 15 r 56 ] ξ= \begin{bmatrix} ξ_1 \\ ξ_2 \\ … \\ ξ_6 \end{bmatrix}, r= \begin{bmatrix} r_{12} \\ r_{13} \\ r_{14} \\ r_{15} \\ r_{56} \end{bmatrix} ξ=⎣⎢⎢⎡ξ1ξ2…ξ6⎦⎥⎥⎤,r=⎣⎢⎢⎢⎢⎡r12r13r14r15r56⎦⎥⎥⎥⎥⎤
最小二乘问题信息矩阵的构成
上述最小二乘问题,对应的高斯牛顿求解为:

注意,这里的 Λ = Σ n e w − 1 ≠ Σ − 1 Λ =Σ_{new}^{-1}≠ Σ ^{−1} Λ=Σnew−1=Σ−1 反应的是求解的方差,而 Σ − 1 Σ ^{−1} Σ−1 反应的是残差的方差。另外,公式中的雅克比矩阵为:

矩阵乘法公式可以写成连加:
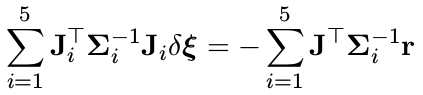
信息矩阵的稀疏性
由于每个残差只和某几个状态量有关,因此,雅克比矩阵求导时,无关项的雅克比为 0。比如
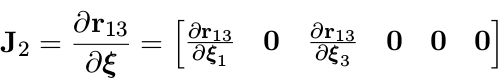

同理,可以计算 Λ 1 Λ _1 Λ1 , Λ 3 Λ _3 Λ3 , Λ 4 Λ_ 4 Λ4 , Λ 5 Λ _5 Λ5 ,并且也是稀疏的。
信息矩阵组装过程的可视化
将五个残差的信息矩阵加起来,得到样例最终的信息矩阵 Λ, 可视化如下:

基于边际概率的滑动窗口算法
为什么 SLAM 需要滑动窗口算法?
- 随着 VSLAM 系统不断往新环境探索,就会有
新的相机姿态以及看到新的环境特征,最小二乘残差就会越来越多,信息矩阵越来越大,计算量将不断增加。 - 为了保持
优化变量的个数在一定范围内,需要使用滑动窗口算法动态增加或移除优化变量。
滑动窗口算法大致流程
- 增加新的变量进入最小二乘系统优化
- 如果变量数目达到了一定的维度,则移除老的变量。
- SLAM 系统不断循环前面两步
疑问:怎么移除老的变量?直接丢弃这些变量吗?
利用边际概率移除老的变量
直接丢弃变量和对应的测量值,会损失信息。正确的做法是使用边际概率,将丢弃变量所携带的信息传递给剩余变量。
下图为 toy expamle 3 中使用边际概率移除变量 ξ 1 ξ _1 ξ1 ,信息矩阵的变化过程:
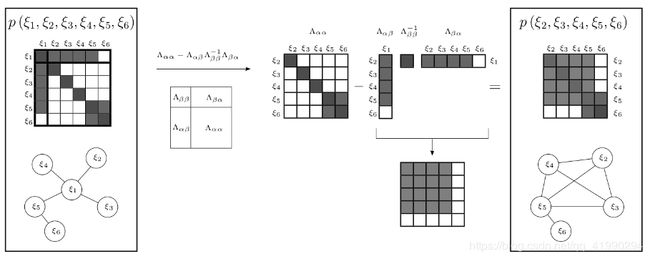
toy example 4
如下图优化系统中,随着 x t + 1 x _{t+1} xt+1 的进入,变量 x t x _t xt 被移除 。
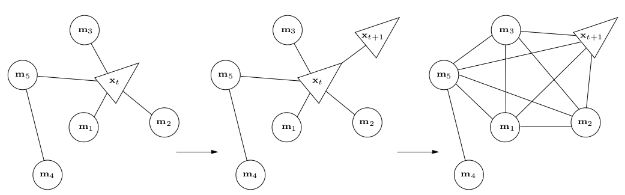

marginalization会使得信息矩阵变稠密!原先条件独立的变量,可能变得相关。
滑动窗口中的 FEJ 算法
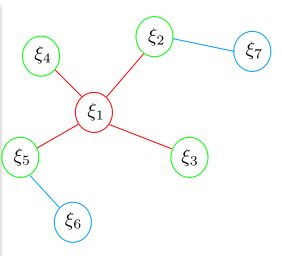
toy example 3 再移除变量 ξ 1 ξ _1 ξ1 后加入新变量

新的变量 ξ 7 ξ _7 ξ7 跟老的变量 ξ 2 ξ _2 ξ2 之间存在观测信息,能构建残差 r 27 r _{27} r27 。图模型如上图所示。
新残差加上之前 marg 留下的信息,构建新的最小二乘系统,对应的信息矩阵的变化如下图所示:

注意: ξ 2 ξ _2 ξ2 自身的信息矩阵由两部分组成,这会使得系统存在
潜在风险。
系统回顾 toy example 3
红色为被marg变量以及测量约束。
绿色为跟 marg 变量有关的保留变量。
蓝色为和 marg 变量无关联的变量。
- 如上图所示,在 t ∈ [ 0 , k ] s t ∈ [0, k]_s t∈[0,k]s 时刻, 系统中状态量为 ξ i ξ_ i ξi , i ∈ [ 1 , 6 ] i ∈ [1, 6] i∈[1,6]。第 k ′ k^ ′ k′时刻,加入新的观测和状态量 ξ 7 ξ _7 ξ7 .
- 在第 k 时刻,最小二乘优化完以后,marg掉变量 ξ 1 ξ _1 ξ1 。被 marg 的状态量记为 x m x _m xm , 剩余的变量 ξ i ξ_ i ξi , i ∈ [ 2 , 5 ] i ∈ [2, 5] i∈[2,5] 记为 x r x _r xr .
- marg 发生以后, x m x _m xm 所有的变量以及对应的测量将被丢弃。同时,这部分信息通过 marg操作传递给了保留变量 x r x _r xr . marg 变量的信息跟 ξ 6 ξ _6 ξ6 不相关。
- 第 k ′ k ^′ k′ 时刻,加入新的状态量 ξ 7 ξ _7 ξ7 (记作 x n x _n xn ) 以及对应的观测,开始新一轮最小二乘优化。
marg 发生后,留下的到底是什么信息?
marg 前,变量 x m x _m xm 以及对应测量 S m S _m Sm 构建的最小二乘信息矩阵为(上文“最小二乘问题信息矩阵的构成”有提到):
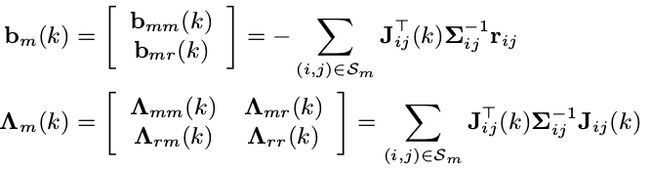
marg 后,变量 x m x _m xm 的测量信息传递给了变量 x r x _r xr (舒尔补):
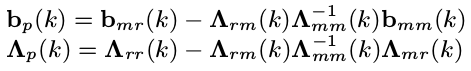
下标 p 表示 prior. 即这些信息将构建一个关于 x r x _r xr 的先验信息。
先验:
我们可以从 b p ( k ) b _p (k) bp(k), Λ p ( k ) Λ _p (k) Λp(k) 中反解出一个残差 r p ( k ) r _p (k) rp(k) 和对应的雅克比矩阵 J p ( k ) J _p(k) Jp(k). 需要注意的是,随着变量 x r ( k ) x _r (k) xr(k) 的后续不断优化变化,残差 r p ( k ) r _p (k) rp(k) 或者 b p ( k ) b _p (k) bp(k)也将跟着变化,但雅克比 J p ( k ) J _p (k) Jp(k) 则固定不变了。
新测量信息和旧测量信息构建新的系统
在 k ′ k ^′ k′ 时刻,新残差 r 27 r _{27} r27 和先验信息 b p ( k ) b _p (k) bp(k), Λ p ( k ) Λ _p (k) Λp(k) 以及残差 r 56 r _{56} r56 构建新的最小二乘问题:
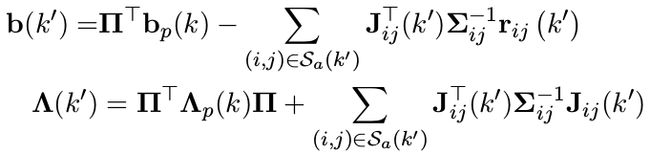
其中 Π = [ I d i m x r 0 ] Π = [I _{dim x _r} 0] Π=[Idimxr0] 用来将矩阵的维度进行扩张。 S a S _a Sa 用来表示除被marg 掉的测量以外的其他测量,如 r 56 r _{56} r56 , r 27 r _{27} r27 。
出现的问题:
由于被 marg 的变量以及对应的测量已被丢弃,先验信息 Λ p ( k ) Λ _p (k) Λp(k)中关于 x r x _r xr 的雅克比在后续求解中没法更新。
但 x r x_r xr 中的部分变量还跟其他残差有联系, 如 ξ 2 ξ_ 2 ξ2 , ξ 5 ξ _5 ξ5 。这些残差如 r 27 r _{27} r27 对 ξ 2 ξ _2 ξ2 的雅克比会随着 ξ 2 ξ _2 ξ2的迭代更新而不断在最新的线性化点处计算。
信息矩阵的零空间变化
滑动窗口算法导致的问题
滑动窗口算法优化的时候,信息矩阵变成了两部分,且这两部分计算雅克比时的线性化点不同。这可能会导致信息矩阵的零空间发生变化,从而在求解时引入错误信息。
比如: 求解单目 SLAM 进行 Bundle Adjustment 优化时,问题对应的信息矩阵 Λ 不满秩,对应的零空间为 N, 用高斯牛顿求解时有
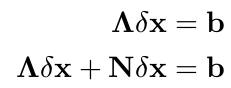
咦,增量 δx 在零空间维度下变化,并不会改变我们的残差。这意味着系统可以有多个满足最小化损失函数的解 x。
toy example
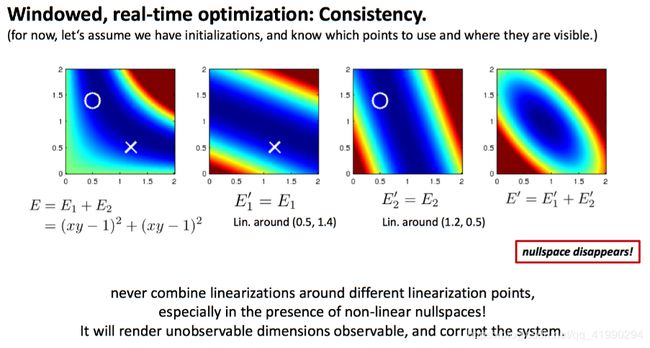
多个解的问题,变成了一个确定解。不可观的变量,变成了可观的。
可观性的一种定义
对于测量系统 z = h ( θ ) + ε z = h(θ) + ε z=h(θ)+ε, 其中 z ∈ R n z ∈ R^n z∈Rn 为测量值, θ ∈ R d θ ∈ R^ d θ∈Rd 为系统状态量,ε 为测量噪声向量。 h ( ⋅ ) h(·) h(⋅) 是个非线性函数,将状态量映射成测量。对于理想数据,如果以下条件成立,则系统状态量 θ 可观:
![]()
对于 SLAM 系统而言(如单目 VO),当我们改变状态量时,测量不变意味着损失函数不会改变,更意味着求解最小二乘时对应的信息矩阵 Λ 存在着零空间。
单目 SLAM 系统 7 自由度不可观:6 自由度姿态 + 尺度。
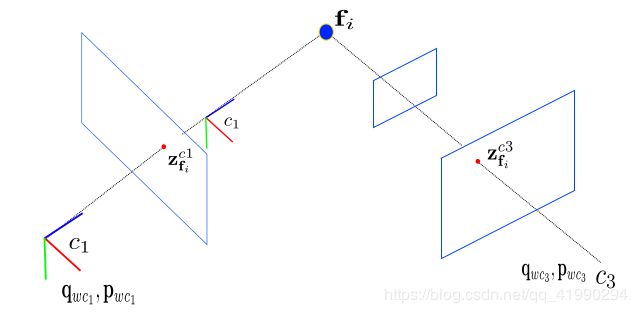
单目 + IMU 系统是 4 自由度不可观:yaw 角 + 3 自由度位置不可观。roll 和 pitch 由于重力的存在而可观,尺度因子由于加速度计的存在而可观。
滑动窗口中的问题
滑动窗口算法中,对于同一个变量,不同残差对其计算雅克比矩阵时线性化点可能不一致,导致信息矩阵可以分成两部分,相当于在信息矩阵中多加了一些信息,使得其零空间出现了变化。
解决办法:First Estimated Jacobian
FEJ 算法:不同残差对同一个状态求雅克比时,线性化点必须一致。这样就能避免零空间退化而使得不可观变量变得可观。
比如: toy example 3 中计算 r 27 r _{27} r27 对 ξ 2 ξ _2 ξ2 的雅克比时, ξ 2 ξ _2 ξ2 的线性话点必须和 r 12 r _{12} r12对其求导时一致。
相关资料:
- David Mackay. “The humble Gaussian distribution”. In: (2006).
- Huang. Conditional and marginal distributions of a multivariate Gaussian. https://gbhqed.wordpress.com/2010/02/21/conditional-and-marginal-distributions-of-a-multivariate-gaussian/
- Matthew R Walter, Ryan M Eustice, and John J Leonard. “Exactly sparse extended information filters for feature-basedSLAM”. In: The International Journal of Robotics Research 26.4 (2007), pp. 335–359.
- Claude Jauffret. “Observability and Fisher information matrix in nonlinear regression”.In: IEEE Transactions on .Aerospace and Electronic Systems 43.2 (2007), pp. 756–759.
- Tue-Cuong Dong-Si and Anastasios I Mourikis. “Consistency analysis for sliding-window visual odometry”. In: 2012 IEEE International Conference on Robotics and Automation. IEEE. 2012, pp. 5202–5209.