VIO学习笔记（五）—— 后端优化实践:逐行手写求解器
学习资料是深蓝学院的《从零开始手写VIO》课程，对课程做一些记录，方便自己以后查询，如有错误还请斧正。由于习惯性心算公式，所以为了加深理解，文章公式采用手写的形式。
VIO学习笔记（一）—— 概述
VIO学习笔记（二）—— IMU 传感器
VIO学习笔记（三）—— 基于优化的 IMU 与视觉信息融合
VIO学习笔记（四）—— 基于滑动窗口算法的 VIO 系统:可观性和 一致性
后端优化实践:逐行手写求解器
- solver 流程回顾
- 非线性最小二乘问题求解:solver
- 高斯牛顿求解流程
- SLAM 问题中高斯牛顿方程的求解
- 利用舒尔补加速 SLAM 问题的求解
- solver 全流程回顾
- solver 求解中的小疑问
- 单目 Bundle Adjustment 求解
- 单目 Bundle Adjustment 求解代码
- 滑动窗口算法
- 滑动窗口算法回顾
- 滑动窗口算法关键步骤可视化
- 滑动窗口算法中关键问题
- 如何更新先验残差?
- VINS-Mono 中的滑动窗口算法
- two way marginalization
solver 流程回顾
非线性最小二乘问题求解:solver
高斯牛顿求解流程
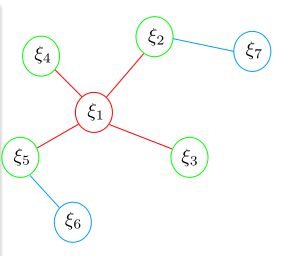
有如下最小二乘系统,对应的图模型如上图所示:
ξ = arg min ξ 1 2 ∑ i ∥ r i ∥ Σ i 2 ξ = \argmin_ξ\frac12 ∑_i∥r _i ∥^ 2_{ Σ_i} ξ=ξargmin21i∑∥ri∥Σi2
对应的高斯牛顿求解,normal equation:
连加形式:
∑ i = 1 n J i ⊤ Σ i − 1 J i δ ξ = − ∑ i = 1 n J ⊤ Σ i − 1 r ∑^n_{i=1}J ^⊤_i Σ_i ^{-1} J_ i δξ = −∑^n_{i=1}J^ ⊤ Σ^{ −1}_i r i=1∑nJi⊤Σi−1Jiδξ=−i=1∑nJ⊤Σi−1r
信息矩阵会存在零空间，因此将会无法使用线性方法求解，如下的slam问题。
SLAM 问题中高斯牛顿方程的求解
利用舒尔补加速 SLAM 问题的求解
直接求解 ∆ x = − H − 1 b ∆x = −H ^{−1 }b ∆x=−H−1b,计算量大（Ｈ矩阵维度将会非常大）。解决办法:舒尔补,利用 SLAM 问题的稀疏性求解。
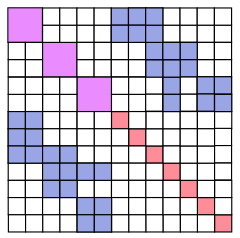
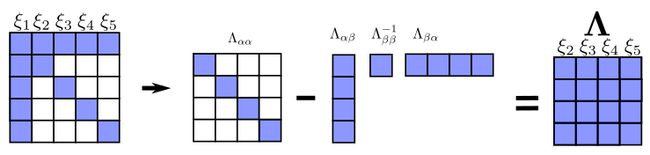
比如,某单目 BA 问题,其信息矩阵如上图所示,可以将其分为:
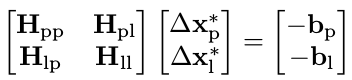
可以利用舒尔补操作,使上式中信息矩阵变成下三角
从而得到:
( H p p − H p l H l l − 1 H p l T ) ∆ x p ∗ = − b p + H p l H l l − 1 b l (H _{pp} − H _{pl }H ^{−1}_{ll} H _{pl}^T )∆x_ p^∗ = −b_ p + H _{pl }H ^{−1}_{ll} b_ l (Hpp−HplHll−1HplT)∆xp∗=−bp+HplHll−1bl
求得 ∆ x p ∗ ∆x_ p ^∗ ∆xp∗ 后,再计算 ∆ x l ∗ ∆x _l ^∗ ∆xl∗ :
H l l ∆ x l ∗ = − b l − H p l ⊤ ∆ x p ∗ H _{ll} ∆x_ l ^∗ = −b_ l − H ^⊤_{pl} ∆x _p^∗ Hll∆xl∗=−bl−Hpl⊤∆xp∗
这样就将要计算的矩阵的维度给减小了，从而减少了计算量。
solver 全流程回顾
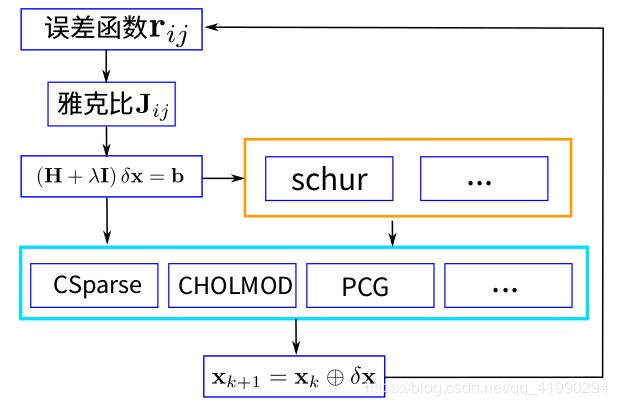
若果是slam问题，则可以利用起信息矩阵的稀疏性，先进性舒尔补，然后进行求解。
solver 求解中的小疑问
上篇博客说到信息矩阵 H 不满秩,那求解的时候如何操作呢?
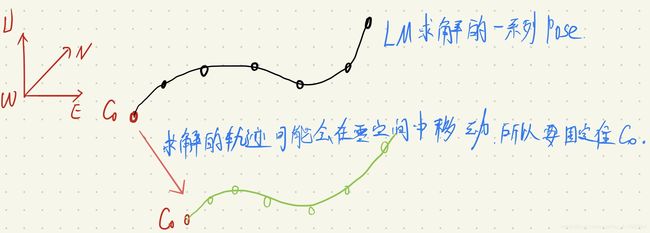
- 使用 LM 算法,加阻尼因子使得系统满秩,可求解,但是求得的结果可能会往零空间变化。
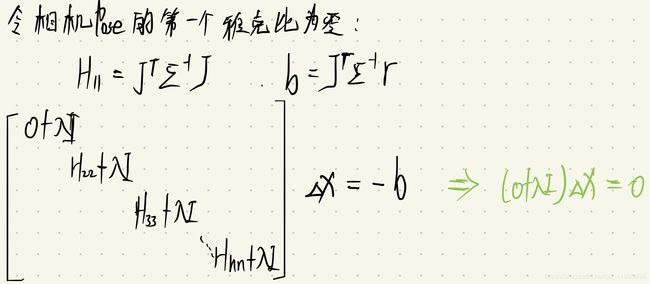
- 添加先验约束,增加系统的可观性。比如 g2o tutorial 中对第一个pose 的信息矩阵加上单位阵 H [ 11 ] + = I H _{[11]} + = I H[11]+=I.
orbslam,svo 等等求 mono BA 问题时,fix 一个相机 pose 和一个特征点,或者 fix 两个相机 pose,也是为了限定优化值不乱飘。那代码如何实现 fix 呢?
- 添加超强先验,使得对应的信息矩阵巨大(如, 1 0 15 10 ^{15} 1015 ),就能使得 ∆ x = 0 ∆x = 0 ∆x=0;
- 设定对应雅克比矩阵为 0,意味着残差等于 0. 求解方程为 ( 0 + λ I ) ∆ x = 0 (0 + λI) ∆x = 0 (0+λI)∆x=0,只能 ∆x = 0。
单目 Bundle Adjustment 求解
核心问题:矩阵块的对应关系,如何拼接信息矩阵。
单目 Bundle Adjustment 求解代码
代码框架和 g 2 o 类似 (相关代码可以参考我的这篇博客)
顶点:vertex
id, 维度,矩阵 index.
边:edge
残差计算
雅克比矩阵计算
保存对应的顶点
求解器:solver
LM 算法
make H, b
线性求解器:QR,SVD,PCG,…
滑动窗口算法
滑动窗口算法回顾
红色为被marg变量以及测量约束。
绿色为跟 marg 变量有关的保留变量。
蓝色为和 marg 变量无关联的变量。
- 如上图所示,在 t ∈ [ 0 , k ] s t ∈ [0, k]_s t∈[0,k]s 时刻, 系统中状态量为 ξ i ξ_ i ξi , i ∈ [ 1 , 6 ] i ∈ [1, 6] i∈[1,6]。第 k ′ k^ ′ k′时刻,加入新的观测和状态量 ξ 7 ξ _7 ξ7 .
- 在第 k 时刻,最小二乘优化完以后,marg掉变量 ξ 1 ξ _1 ξ1 。被 marg 的状态量记为 x m x _m xm , 剩余的变量 ξ i ξ_ i ξi , i ∈ [ 2 , 5 ] i ∈ [2, 5] i∈[2,5] 记为 x r x _r xr .
- marg 发生以后, x m x _m xm 所有的变量以及对应的测量将被丢弃。同时,这部分信息通过 marg操作传递给了保留变量 x r x _r xr . marg 变量的信息跟 ξ 6 ξ _6 ξ6 不相关。
- 第 k ′ k ^′ k′ 时刻,加入新的状态量 ξ 7 ξ _7 ξ7 (记作 x n x _n xn ) 以及对应的观测,开始新一轮最小二乘优化。
滑动窗口算法关键步骤可视化
步骤 1:构建先验
步骤 2:先验 + 新测量信息 → 新的信息矩阵
和直接 Bundle Adjustment 相比,多了一个先验矩阵的维护。
滑动窗口算法中关键问题
如何更新先验残差?
目的:
虽然先验信息矩阵固定不变,但随着迭代的推进,变量被不断优化,先验残差需要跟随变化。否则,求解系统可能崩溃。
方法:
先验残差的变化可以使用一阶泰勒近似。
VINS-Mono 中的滑动窗口算法
two way marginalization
- 当滑动窗口中第二新的图像帧为关键帧,则 marg 最老的帧,以及上面的路标点。
- 当滑动窗口中第二新的图像帧不是关键帧,则丢弃这一帧上的视觉测量信息,IMU 预积分传给下一帧。
相关资料：
- Giorgio Grisetti et al. “A tutorial on graph-based SLAM”. In: IEEE Intelligent Transportation Systems Magazine 2.4(2010), pp. 31–43.
- Rainer Kümmerle et al. “g 2 o: A general framework for graph optimization”. In: 2011 IEEE International Conference on Robotics and Automation. IEEE. 2011, pp. 3607–3613.
- Manolis IA Lourakis and Antonis A Argyros. “SBA: A software package for generic sparse bundle adjustment”.In: ACM Transactions on Mathematical Software (TOMS) 36.1 (2009), p. 2.
- Giorgio Grisetti et al. “g2o: A general framework for (hyper) graph optimization”.In:Tech. Rep. (2011).
- Tong Qin, Peiliang Li, and Shaojie Shen. “Vins-mono: A robust and versatile monocular
visual-inertial state estimator”.In: IEEE Transactions on Robotics 34.4 (2018), pp. 1004–1020. - Zichao Zhang, Guillermo Gallego, and Davide Scaramuzza. “On the comparison of gauge freedom handling
in optimization-based visual-inertial state estimation”. In: IEEE Robotics and Automation Letters 3.3 (2018),pp. 2710–2717.