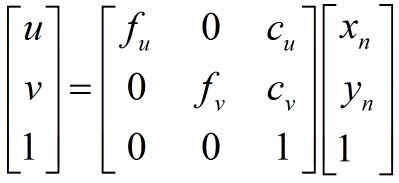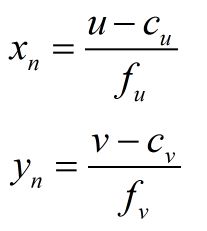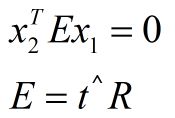高翔Slambook第七讲代码解读(2d-2d位姿估计)
前言:小白创建了一个微信公众号,主要面向学习视觉的小伙伴,分享一些学习过程中的感受和一些技术文章。公众号里文章也会更新在CSDN中,不过由于工作量较大,会出现一段时间的延时,感兴趣的小伙伴可以关注公众号第一时间接受消息。
作者:小白
公众号:小白学视觉
![]()
SLAM前端,或者说视觉里程计VO,做的最主要的一件事就是计算或者估计两帧图像之间的位姿变换,也即旋转矩阵R和平移向量t。根据所应用于计算的特征点信息的不同,可分为三类:2d-2d类、3d-2d类、3d-3d类,这取决于我们手头所现有的能拿来做位姿计算的数据形式。倘若我们只知道某个特征点在相机成像平面的位置,也即像素坐标或归一化平面坐标,却不知其深度,那么这将是一个只具备2d信息的特征点;如果我们通过三角化计算,或者通过RGB-D相机直接测得了某点的深度信息,结合其2d信息,我们能够推算其在该帧图像的相机坐标系下的位置,即相机坐标,此时便形成了一个具备3d信息的特征点。
我们不妨首先来看一下2d-2d位姿估计的过程。关于其中所使用的对极几何、对极约束等数学推算,小绿在此不做赘述,而是将重点放在代码上。
先把子函数声明与主函数放在这里:
#include
#include
#include
#include
#include
using namespace std;
using namespace cv;
void find_feature_matches (
const Mat& img_1, const Mat& img_2,
std::vector& keypoints_1,
std::vector& keypoints_2,
std::vector< DMatch >& matches );
void pose_estimation_2d2d (
const std::vector & keypoints_1,
const std::vector & keypoints_2,
const std::vector< DMatch > & matches,
Mat& R, Mat& t );
void verify_polar_constraint(
const std::vector & keypoints_1,
const std::vector & keypoints_2,
const Mat& R, const Mat& t,
const std::vector & matches );
// 像素坐标转相机归一化坐标
Point2d pixel2cam ( const Point2d& p, const Mat& K );
int main ( int argc, char** argv )
{
if ( argc != 3 )
{
cout<<"usage: pose_estimation_2d2d img1 img2"< keypoints_1, keypoints_2;
vector matches;
find_feature_matches ( img_1, img_2, keypoints_1, keypoints_2, matches );
cout<<"一共找到了"< 可以看出这里在主函数之外声明了4个函数:find_feature_matches、pose_estimation_2d2d、verify_polar_constraint、pixel2cam。
其中find_feature_matches完全是由feature_extraction.cpp封装成的函数:对存储图像的两个Mat型变量、存储特征点信息的两个vector
pose_estimation_2d2d函数则是本程序中的重头戏:在传递入特征点数据容器keypoints_1与keypoints_2、特征点配对信息容器matches后,进行计算并存入Mat类旋转矩阵R与平移向量t。其内部原理我们稍后会回过头来细细分析。
verify_polar_constraint函数则是在解算出R、t后,将其带回到特征点坐标中,来验算是否满足对极约束的一个过程。在验算过程中其函数内部调用了坐标变换函数pixel2cam(这不是opencv提供的),用来将像素坐标通过相机内参转化为归一化成像平面坐标。
那么对于主函数,其主要操作也可以简单列举如下:读取图像->初始化变量->寻找特征点->计算相机位姿变换->验证计算结果。下面我们来逐步解读各个子函数。
pixel2cam
Point2d pixel2cam ( const Point2d& p, const Mat& K )
{
return Point2d
(
( p.x - K.at ( 0,2 ) ) / K.at ( 0,0 ),
( p.y - K.at ( 1,2 ) ) / K.at ( 1,1 )
);
} 调用这个函数会返回一个cv::Point2d类的变量,而Point2d类的变量会存储一个2d点的xy坐标,即有两个成员变量.x和.y,类型为double。在此函数中,直接return了一个通过Point2d构造的变量,而并没有先定义变量再返回(我竟然连这个都要感叹一下)。
而这个函数内部则使用了像素坐标、归一化平面坐标与相机内参的等式关系:
即
其中,使用K.at
pose_estimation_2d2d(本程序的主要计算环节)
void pose_estimation_2d2d ( const vector< KeyPoint >& keypoints_1, const vector< KeyPoint >& keypoints_2, const vector< DMatch >& matches, Mat& R, Mat& t )
{
// 相机内参,TUM Freiburg2
Mat K = ( Mat_ ( 3,3 ) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1 );
//-- 把匹配点转换为vector的形式
vector points1;
vector points2;
for ( int i = 0; i < ( int ) matches.size(); i++ )
{
points1.push_back ( keypoints_1[matches[i].queryIdx].pt );
points2.push_back ( keypoints_2[matches[i].trainIdx].pt );
}
//-- 计算基础矩阵
Mat fundamental_matrix;
fundamental_matrix = findFundamentalMat ( points1, points2, CV_FM_8POINT );
cout<<"fundamental_matrix is "< 这里
Mat K = ( Mat_ ( 3,3 ) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1 ); 在定义Mat类变量K时直接进行了初始化,调用Mat_类构造函数并规定好元素类型为double,然后通过<<将元素依次传递进去,外面套上括号避免编译出错。
由于在进行对极几何计算时,需要使用特征点的2d坐标,而此时两帧图像中的特征点坐标还保存在两个存储KeyPoint类对象的容器keypoints_1和keypoints_2中,因此我们需要将其中的特征点坐标信息提取出来(方便一会使用OpenCV提供的计算函数进行计算):
vector points1;
vector points2;
for ( int i = 0; i < ( int ) matches.size(); i++ )
{
points1.push_back ( keypoints_1[matches[i].queryIdx].pt );
points2.push_back ( keypoints_2[matches[i].trainIdx].pt );
} 这里特征点坐标按照Point2f进行存储,因为在keypoints_1中存储的点的坐标(keypoints_1[0].pt)是Point2f类型的,因此定义两个存储Point2f类型对象的容器points1与points2。在坐标值的存储循环中,以i=0为例:
points1.push_back ( keypoints_1[matches[0].queryIdx].pt );
points2.push_back ( keypoints_2[matches[0].trainIdx].pt );调用容器对应的push_back()函数将括号内的值加入到容器的尾部。此时加入的值分别为keypoints_1[matches[0].queryIdx].pt与keypoints_2[matches[0].trainIdx].pt,分别为第一对特征点对(角标从0开始,i=0对应第一对特征点对)中,前一帧(查询图像)中的特征点索引在keypoints_1中对应的特征点坐标,与后一帧(训练图像)中的特征点索引在keypoints_2中对应的特征点坐标(有点啰嗦)。
//-- 计算基础矩阵
Mat fundamental_matrix;
fundamental_matrix = findFundamentalMat ( points1, points2, CV_FM_8POINT );
cout<<"fundamental_matrix is "<进而,调用OpenCV提供的基础矩阵计算函数findFundamentalMat,按照八点法进行计算,并返回一个4×4的F矩阵fundamental_matrix。
//-- 计算本质矩阵
Point2d principal_point ( 325.1, 249.7 ); //相机光心, TUM dataset标定值
double focal_length = 521; //相机焦距, TUM dataset标定值
Mat essential_matrix;
essential_matrix = findEssentialMat ( points1, points2, focal_length, principal_point );
cout<<"essential_matrix is "<同理,调用OpenCV提供的本质矩阵计算函数findEssentialMat计算本质矩阵essential_matrix。由于计算本质矩阵E时需要提供归一化平面坐标,因此需要将像素坐标转化成归一化平面坐标,需要提供相机内参cu、cv与f。
//-- 从本质矩阵中恢复旋转和平移信息.
recoverPose ( essential_matrix, points1, points2, R, t, focal_length, principal_point );
cout<<"R is "<最后,通过OpenCV提供的R、t计算函数recoverPose计算R和t。由于函数默认使用本质矩阵进行解算,因此需要传入E。
verify_polar_constraint
void verify_polar_constraint(
const vector< KeyPoint >& keypoints_1, const vector< KeyPoint >& keypoints_2, const Mat& R, const Mat& t, const vector< DMatch >& matches )
{
//-- 验证E=t^R*scale
Mat t_x = ( Mat_ ( 3,3 ) <<
0, -t.at ( 2,0 ), t.at ( 1,0 ),
t.at ( 2,0 ), 0, -t.at ( 0,0 ),
-t.at ( 1,0 ), t.at ( 0,0 ), 0 );
cout<<"t^R="< ( 3,3 ) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1 );
for ( DMatch m: matches )
{
Point2d pt1 = pixel2cam ( keypoints_1[ m.queryIdx ].pt, K );
Mat y1 = ( Mat_ ( 3,1 ) << pt1.x, pt1.y, 1 );
Point2d pt2 = pixel2cam ( keypoints_2[ m.trainIdx ].pt, K );
Mat y2 = ( Mat_ ( 3,1 ) << pt2.x, pt2.y, 1 );
Mat d = y2.t() * t_x * R * y1;
cout << "epipolar constraint = " << d << endl;
}
} 这里是为了验证刚才所计算得到的R和t是否满足对极约束:
这里有一个循环条件语句:
for ( DMatch m: matches )
{
...
}使用for循环对vector
下面来看一下程序运行结果:
根据两帧图像中筛选出的79对特征点对,计算出了基础矩阵F和本质矩阵E,以及单应矩阵H(这里特征点不属于共面情况,因此单应矩阵H的计算无法用来求解R、t)。进而求解出相机位姿变换R、t,并通过计算验证了各对特征点是否满足对极约束,结果是满足的。
好了,对pose_estimation_2d2d.cpp的解读就先到这里。可以看出程序并不复杂,所用的语句也相对基本,真正的难题在后续会越来越多。由此,小绿希望在细xiao细ti梳da理zuo的同时,能够与大家一同进步!
![]()