抽象数据类型ADT(栈与队列)

抽象数据类型 abstract data type,ADT:

指只通过接口进行访问的数据类型，我们将那些使用ADT的程序叫做客户，将那些确定数据类型的程序叫做实现。

数据的表示和实现操作函数都在接口的实现里面，和客户完全分离。接口对于我们来说是不透明的：客户不能通过接口看到方法的实现。

优点：

1. 将编程时对数据的概念转换从任何特定的数据表示和算法实现中分离出来。
2. 使用抽象机制可以让我们关心程序如何实现的细节上得到解放。
3. 当程序的性能重要时，我们需要知道基本操作的开销。

栈ADT的实现

栈ADT的实现有两种方式，一是数组实现，二是链表实现。

使用数组实现时，将数据项放进数组中，记录栈顶位置的下标。进行进栈push操作时，只要把项存放到栈顶下标所指示的位置即可，然后下标增1；进行弹栈pop操作时，使下标减1，并返回它所指示的项。初始Initialize操作包含分配指定大小数组，测试是否为空empty操作包含检查下标是否为0.

数组实现的缺点是在使用之前需要知道数组的最大长度，这样才能分配内存。

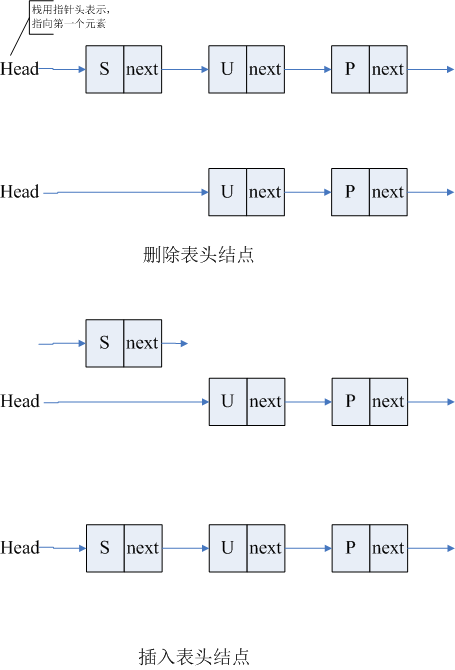
使用链表实现时，对于pop操作，删除链表表头元素，并返回其项；对于push操作，创建一个节点，然后把其添加到表头。

下推栈的数组实现

当栈中有N个项时，这一实现把这些项保存在s[0],...,s[N-1]中，按照最近插入的顺序排列。栈顶（下一个进栈元素将要占据的位置）元素就是s[N].

static Item *s;
static int N;

void STACHKinit(init maxN)
{
	s=malloc(maxN * sizeof(Item));//为数组分配固定maxN个空间，首地址记录在s中。
	N=0;//当前栈顶位置
}

int STACHKempty()
{
	return N == 0;
}

void STACHKpush(Item item)
{
	s[N++] = item;//先加入，再++
}

Item STACKpop()
{
	return s[--N];//先弹出，再--
}

下推栈的链表实现

typedef struct STACKnode* link;
struct STACKnode
{
	Item item;
	link next;
};
static link head;

link NEW(Item item,link next)
{
	link x = malloc(sizeof *x);//分配一个节点
	x->item = item;//节点中填充数据
	x->next = next;//节点中填充下一个指针
	
	return x;
}

void STACKinit()
{
	head = NULL;
}

int STACKempty()
{
	return head == NULL;//check head 是否为 NULL
}

STACKpush(Item item)
{
	head = NEW(item,head);//分配一个节点，填入数据，放入链表头（下一个指针为head）,并更新成为新的表头。
}


Item STACKpop()
{
	Item item = head->item;//需要pop的元素
	link temp = head->next;//记录下一个，防止free(head)的时候把下一个丢失。
	free(head);//释放栈顶节点（该节点数据已经被记录在item中）
	head=temp;//下下个节点成为新的head
	
	return item;
}

FIFO队列的实现

FIFO(first in first out,先进先出)：包含两个基本操作，插入（put）一个新的项，删除（get）一个最早插入的项。

FIFO队列链表实现

我们在链表上维持两个指针，一个在开始（我们可以删除第一个元素），一个在末尾（我们可以插入一个新的元素）。

typedef struct QUEUEnode* link;
struct QUEUEnode
{
	Item item;
	link next;
};
static link head,tail;

link NEW(Item item,link next)
{
	link x = malloc(sizeof *x);//分配一个节点
	x->item = item;//节点中填充数据
	x->next = next;//节点中填充下一个指针
	
	return x;
}

void QUEUEinit()
{
	head = NULL;
}

int QUEUEempty()
{
	return head == NULL;//check head 是否为NULL
}

QUEUEput(Item item)
{
	if (head == NULL)
	{
		head = tail = NEW(item,head);//对于插入空队列，头尾指针指向同一个新插入的元素。
		return;
	}
	tail->next = NEW(item,tail>next);//对于非空队列,在尾部插入元素
	tail = tail->next;//插入的元素更新为新的尾部。
}


Item QUEUEget()
{
	Item item = head->item;//需要pop的元素
	link temp = head->next;//记录下一个，防止free(head)的时候把下一个丢失。
	free(head);//释放栈顶节点（该节点数据已经被记录在item中）
	head=temp;//下下个节点成为新的head
	
	return item;
}

FIFO队列数组实现

给数组维持两个索引的下标：一个在队列头，一个在队列尾。我们把队列的内容看成两个下标之间的元素。为了删除一个元素，我们把它从队列的开始（头部）删除，然后使头索引增1。为了插入一个元素，我们把它加到队列的最后（尾部），然后使尾索引增1。

当到达数组的末尾时，我们使它回到数组的开始部分。

如果head和tail重合，我们认为此时队列为空。

如果put操作使它们相等，则认为队列满。

static Item *q;
static int N,head,tail;
void QUEUEinit(int maxN)
{
	q = malloc((maxN + 1) * sizeof(Item));//事先为数组分配maxN + 1个节点空间
	N = maxN+1;
	head = N;
	tail = 0;
}

int QUEUEempty()
{
	return head % N == tail;
}
	
void QUEUEput(Item item)
{
	q[tail++] = item;
	tail = tail % N;//若tail < N,则tail % N == tail;  若tail >= N,则tail % N == 回卷到头部开始计算
}	

Item QUEUEget()
{
	head = head % N;//若head < N,则head % N == tail;  若head >= N,则head % N == 回卷到头部开始计算
	return q[head++];//返回节点后推进一个
}