在工作中,我们最佩服的一群人就是那种只用“纸和笔”就能把问题说清楚甚至解决的人,这需要超强的理论基础以及模型抽象能力——一言不合就上公式,简单、粗暴、有效。
今天,我们也来装一装X,看看如何通过简单“写写画画”来设计一个FIR滤波器。
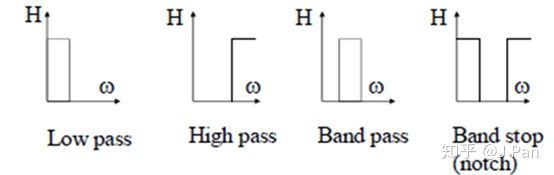
滤波器的概念相比大家都很熟悉了,一般按照频率特性可以分为低通、高通、带通及带阻滤波器,这是从输出特性来说的。
设计常规滤波器的时候,我们一般采用另外一种分类,FIR(Finite Impulse Response)和IIR(Infinite Impulse Response)filter,即有限脉冲响应滤波器和无限脉冲响应滤波器。前面的文章中,我们已经介绍了,理想脉冲信号,其傅里叶变换恒为1,也就时包含了所有频率分量,是一个理想的测试信号,能够激发出所有单位频率分量的响应,因此理想脉冲信号的响应,就代表了系统的特性。
滤波器也可以看成一个系统,如果用一个理想脉冲信号激励,就会有输出,我们把输出个数有限的称为有限脉冲响应滤波器(FIR);输出无限多的称为无限脉冲响应滤波器(IIR)。今天先说一下FIR。
一、Z传递函数的零点和极点代表什么
我们知道 域的零极点表征了系统的响应特性:极点代表了系统的模态,零点代表了系统能屏蔽的模态,具体参看文章
J Pan:如何入门自动控制理论
在“如何理解离散傅里叶变换及z变换”一文中,
J Pan:如何理解离散傅里叶变换及Z变换
我们介绍了 域和 域的关系: , ,所以
当 时, ,对应的是 域的虚轴,而此时 对应的是单位圆,也就是说 变换将 域的虚轴映射成 域的单位圆。
当 时, ,对应的是 域的正半轴,而此时 ,由于 ,也就是说此时 变换将 域正半轴映射到了 域的单位圆外部。
当 时, ,对应的是 域的负半轴,而此时 ,由于 ,也就是说此时 变换将 域负半轴映射到了 域的单位圆内部。
继续扩展, ,很显然:
- 当 时 ;
- 当 时 ;
- 当 时 ;
- 当 时 ;
我们知道在 域上,虚轴上不同的点对应不同的频率,而 域上单位圆与 域虚轴对应,可见, 域单位圆上不同的点,代表了不同的频率。
很容易得到,对于 域的传递函数的零极点,也有和 域零极点类似的结论:
- 规律1:如果在单位圆上有零点,则在零点所对应的频率上幅值响应为零;
- 规律2:对于不在单位圆上的零点,在单位圆上离零点最近的点对应的频率上幅值响应最小。
- 规律3:对于在单位圆内部的极点,在单位圆上离极点最近的点对应的频率上幅值响应最大。
- 规律4:如果极点和零点重合,对系统的频率响应没有影响。
在“如何理解离散傅里叶变换及z变换”一文中,我们还介绍了如果一个信号的频谱如下:
频谱中最大的频率为 ,用一个周期为 狄拉克梳状函数进行采采样后的频谱为原频谱的周期延拓,延拓的周期为采样周期 ,示意图如下:
也就是说,采样之后的频谱是一个周期函数,我们把 称为主值区间,其中 是 延拓一个 周期得来的,与 完全对称,因此我们一般只考虑 区间,也就是半个单位圆的区域。
二、零、极点分布如何影响频率响应
我们先看个简单的例子,熟悉一下套路。
Ex1:
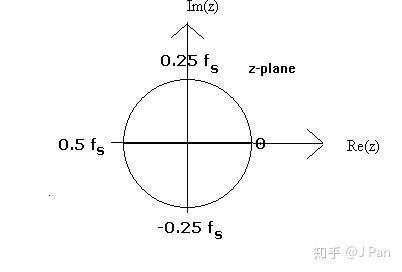
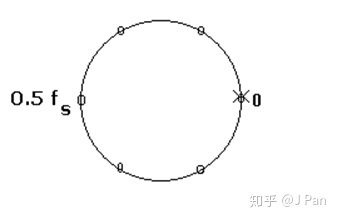
对于这个系统,在 有一个极点,在 时有一个零点。零、极点分布如下:
其中 表示零点, 表示极点。我们来粗略分析一下这个系统的响应会是什么样。从 也就是单位圆上角度为零(也是频率为零)的点开始,此处有一个零点,根据规律1,显然在频率为零时系统响应为零,顺着单位圆沿逆时针方向旋转,我们离零点越来越远,零点的影响也越来越小,因此幅值响应会逐渐增大。当我们到达 ,也就是频率为 时,此时离零点最远,因此响应会达到一个最大值,当频率继续增大时,由于离零点又开始接近了,幅值响应又开始变小。
细心的童鞋可能发现了另外一个端倪,你刚分析了零点,可系统明明还有一个极点啊!——没错,为你的细心点赞——我们仔细观察,发现极点正好位于圆心位置,也就是说所有频率段离极点的距离都一样,因此可以认为都没影响。
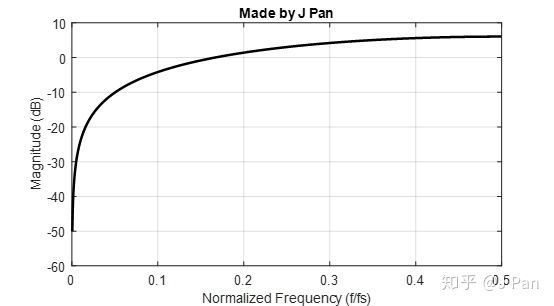
用freqz函数将系统的频响画出来,就长成下图的样子,这也印证了我们之前的分析,这个系统本质上是一个高通滤波器。
%%
clc;clear; fs=1e4;b=[1 -1];a=[0 1]; [h,f] = freqz(b,a,2001,'whole',fs);N=round(0.5*length(h)); plot(f(1:N)/fs,20*log10(abs(h((1:N)))),'linewidth',2,'color','k'); ax = gca;ax.YLim = [-60 10];ax.XTick = 0:.1:0.5; xlabel('Normalized Frequency (f/fs)');ylabel('Magnitude (dB)'); grid on;title('Made by J Pan') 这个系统换做时域是什么样?
若 为系统输出, 为系统输入,则
进行逆变换就可以得到:
这本质就是一个差分,对应连续系统的微分,我们知道微分对应的是传递函数是 ,稳态时为 ,这显然是一个高通滤波器,与前面的分析是一致的。
Ex2:
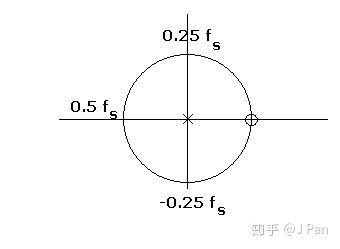
很容易看出系统的零极点图如下:
显然,零点跑到了 处,因此,系统的频响会先减小,到 处达到最小值,然后又增加,具体频响如下图,这本质上是一个低通滤波器。
![]()
%%
clc;clear; fs=1e4;b=[1 1];a=[0 1]; [h,f] = freqz(b,a,2001,'whole',fs);N=round(0.5*length(h)); plot(f(1:N)/fs,20*log10(abs(h((1:N)))),'linewidth',2,'color','k'); ax = gca;ax.YLim = [-60 10];ax.XTick = 0:.1:0.5; xlabel('Normalized Frequency (f/fs)');ylabel('Magnitude (dB)'); grid on;title('Made by J Pan') 很容易得到时域的表达式为:
这本质就是一个离散求和,对应连续系统的积分,我们知道微分对应的是传递函数是 ,稳态时为 ,这显然是一个低通滤波器,与前面的分析是一致的。
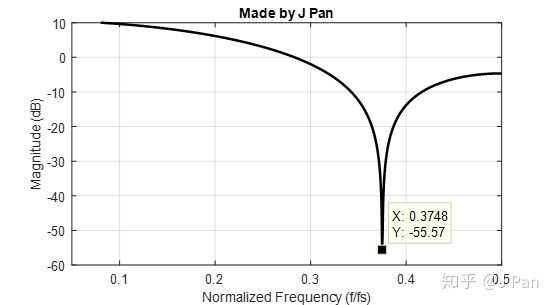
Ex3:假如我们在0到 之间放置一个零点,那会不会是一个带阻滤波器呢?比如我们想在频率在 这个点的系统频率响应为零。
频率 所在点对应的相角为 ,由第一部分可知,频率响应在 与 之间具有对称性,因此上述系统在相角为 处也有一个零点。
转化成传递函数就是:
展开可以获得:
即
%%
clc;clear; fs=1e4;b=[1 sqrt(2) 1];a=[0 0 1]; [h,f] = freqz(b,a,2001,'whole',fs);N=round(0.5*length(h)); plot(f(1:N)/fs,20*log10(abs(h((1:N)))),'linewidth',2,'color','k'); ax = gca;ax.YLim = [-60 10];ax.XTick = 0:.1:0.5; xlabel('Normalized Frequency (f/fs)');ylabel('Magnitude (dB)'); grid on;title('Made by J Pan') 这个系统换做时域是什么样?
若 为系统输出, 为系统输入,则
进行逆变换就可以得到:
Ex4:
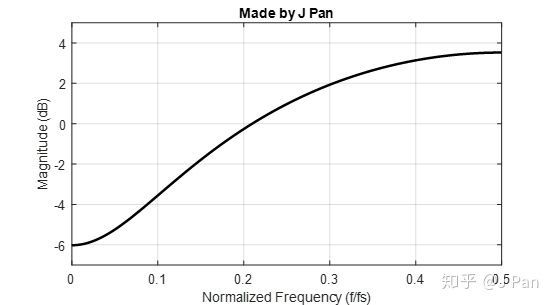
前面,我们把零点和极点都放在了单位圆上,那能不能放在其他位置呢?——单位圆外面是不行的,因为外面对应着s域的正半轴,系统是不稳定;内部呢?我不妨把零点先放在x轴上试试,放在 这个点上。
粗略分析,当 时(对应频率为零)离零点最近,此时频率响应应该最小,但不为零。当 时(对应 )离零点最远,响应应该到达最大值。
可见,零极点的位置决定了系统在不同频率下的响应情况。
%%
clc;clear; fs=1e4;b=[1 -0.5];a=[0 1]; [h,f] = freqz(b,a,2001,'whole',fs); N=round(0.5*length(h)); plot(f(1:N)/fs,20*log10(abs(h((1:N)))),'linewidth',2,'color','k'); ax = gca;ax.YLim = [-7 5];ax.XTick = 0:.1:0.5; xlabel('Normalized Frequency (f/fs)'); ylabel('Magnitude (dB)'); grid on;title('Made by J Pan') Ex5:
这个传递函数有点意思了,它有6个根——都是复数哦!
我们可以将上述方程写成如下格式:
所以解为:
总共有6个根均布在单位圆上,如下图:
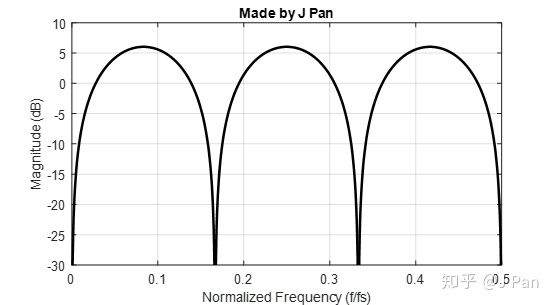
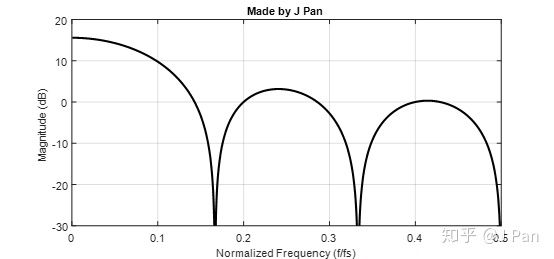
我们可以画出如下的频率响应,可见其本质是一个多个带阻的滤波器。这种滤波器有啥用呢?我们知道,市电频率是50Hz,其带来的干扰一般就是50Hz其整数倍谐波100Hz、150Hz,200Hz等,选择这种数字滤波器就可以消除类似于市电50Hz带来的噪声影响。
%%
clc;clear; fs=1e4;b=[1 0 0 0 0 0 -1];a=[0 0 0 0 0 0 -1]; [h,f] = freqz(b,a,2001,'whole',fs); N=round(0.5*length(h)); plot(f(1:N)/fs,20*log10(abs(h((1:N)))),'linewidth',2,'color','k'); ax = gca;ax.YLim = [-30 10];ax.XTick = 0:.1:0.5; xlabel('Normalized Frequency (f/fs)'); ylabel('Magnitude (dB)'); grid on;title('Made by J Pan')
Ex6:
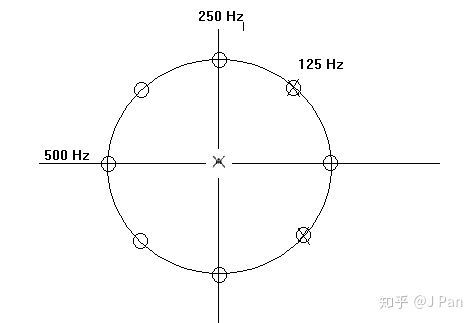
对于该函数,其零点位于 处,6个零点均匀分布在单位圆上。
另外,在 处还有一个极点,与该处的零点重合,零极点如下图所示。
可见,在 处由于零极点重合,并未对系统产生影响,也就是说,如果想消除某零点给系统带来的影响,我们可以再该位置同时也放置一个极点;反之亦然。
观察一下与Ex5的频响的区别,是不是很有意思?
clc;clear;
fs=1e4;b=[1 0 0 0 0 0 -1];a=[0 0 0 0 0 1 -1]; [h,f] = freqz(b,a,2001,'whole',fs); N=round(0.5*length(h)); plot(f(1:N)/fs,20*log10(abs(h((1:N)))),'linewidth',2,'color','k'); ax = gca;ax.YLim = [-30 20];ax.XTick = 0:.1:0.5; xlabel('Normalized Frequency (f/fs)'); ylabel('Magnitude (dB)'); grid on;title('Made by J Pan')
三、如何简单粗暴的设计一个FIR滤波器
前面套路差不多说完了——有高通、低通、带阻滤波器,好像还没有带通滤波器,下面我们就拿带通滤波器来练练手。
要求如下:在125Hz时频率响应达最大值,采样频率 。
由于125Hz是采样频率1000Hz的1/8,我们先均匀布置8个零点在单位圆上,这样就能保证有一个零点是位于125Hz处的。
我们知道,零点位置时频率响应最小的点,我们现在是想要在125Hz(相角 )处响应最大,貌似有矛盾——没关系,我们可以再放个极点,将这个零点抵消掉(规律4)!
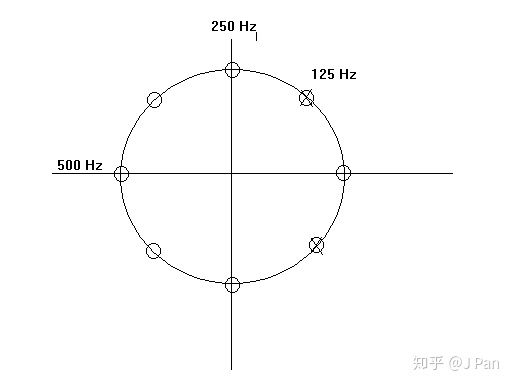
由于对称性呢,在-125Hz(相角 )也要放置一个极点。最终零、极点分布如下图:
由Ex5可知,均匀分布的8个点,对应的传递函数的分子为 ,两个极点对应传递函数的分母为 ,所以总的传递函数为:
化简一下:
这就是我们要的传递函数了,换成时域是什么样呢?
逆变换一下:
平移一下:
即
细心地童鞋可能注意到: 是未来的数啊,这显然不太合理,那怎么办呢?——还记得Ex1吗?我们可以再圆点处加极点啊,当其他零极点都在单位圆上时不影响频率响应,如下图:
则传递函数变成了:
最终时域关系变为了:
%%
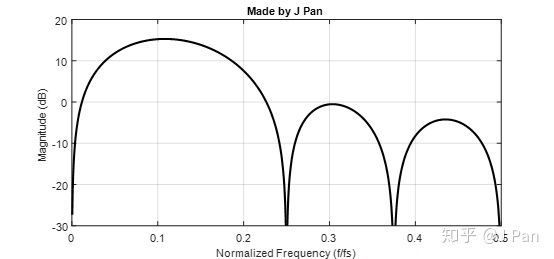
clc;clear; fs=1e4;b=[1 0 0 0 0 0 0 0 -1];a=[1 -sqrt(2) 1]; [h,f] = freqz(b,a,2001,'whole',fs); N=round(0.5*length(h)); plot(f(1:N)/fs,20*log10(abs(h((1:N)))),'linewidth',2,'color','k'); ax = gca;ax.YLim = [-30 20];ax.XTick = 0:.1:0.5; xlabel('Normalized Frequency (f/fs)'); ylabel('Magnitude (dB)'); grid on;title('Made by J Pan') 怎么样,读到这的时候你是不是已经开始跃跃欲试了?那就开始拿起笔和纸,试试吧!
转载自知乎——讲的真是通俗易懂,膜拜啊。